A) Физический смысл стационарной задачи
Уравнение вида: 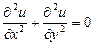 или
или 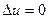 - называется уравнением Лапласа. Оно описывает стационарный процесс с установившимся распределением температуры сплошной среды. Описывает любые установившиеся процессы. При наличии источников тепла получаем уравнение:
- называется уравнением Лапласа. Оно описывает стационарный процесс с установившимся распределением температуры сплошной среды. Описывает любые установившиеся процессы. При наличии источников тепла получаем уравнение: 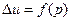 - неоднородное уравнение Лапласа – уравнение Пуассона.
- неоднородное уравнение Лапласа – уравнение Пуассона.
B) Примеры
Уравнение теплопроводности: 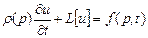 - описывает распределение температуры в сплошной среде. Если это распределение не зависит от времени, то уравнение теплопроводности примет вид:
- описывает распределение температуры в сплошной среде. Если это распределение не зависит от времени, то уравнение теплопроводности примет вид: 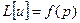 . Аналогично для колебаний.
. Аналогично для колебаний.
C) Понятие о потенциалах
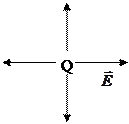 | Заряд в точке Q создаёт поле, которое описывается потенциалом 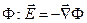 , а этот потенциал , а этот потенциал 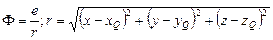 , r – расстояние от точки Q до некоторой точки р. Величина , r – расстояние от точки Q до некоторой точки р. Величина 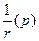 удовлетворяет уравнению Лапласа для всех удовлетворяет уравнению Лапласа для всех 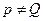 : :  . То же самое можно сказать о потенциале системы зарядов - это есть сумма потенциалов отдельных зарядов. . То же самое можно сказать о потенциале системы зарядов - это есть сумма потенциалов отдельных зарядов. |
D) Постановка задач
Постановка задачи (можно поставить задачу для разного числа переменных) состоит из составления уравнения и определения области изменения переменных.
Начальных условий здесь не будет, т.к. задача стационарная, а граничные условия не будут зависеть от времени:
Пишем уравнение: 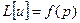
Задаём область: пусть некоторая область D ограничена контуром Г, p – внутренние точки области D: 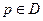 .
.
Задаём краевые условия: 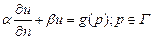 (линейное краевое условие).
(линейное краевое условие).
Первая краевая задача: 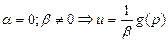 - температура на границе
- температура на границе
Вторая краевая задача: 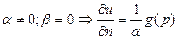 - поток тепла через границу
- поток тепла через границу
Третья краевая задача: 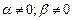
2. Первая и вторая формулы Грина с оператором 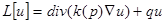 , следствия.
, следствия.
Пусть функции u,v дважды непрерывно дифференцируемы. Введём скалярное произведение: 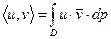 .
.
Формулы Грина:
1. Применим к u оператор L и перемножим скалярно с v: 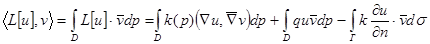 . Выведем эту формулу. Распишем скалярное произведение:
. Выведем эту формулу. Распишем скалярное произведение: 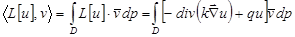 . Рассмотрим отдельно первое слагаемое:
. Рассмотрим отдельно первое слагаемое: 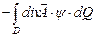 . Для того чтобы воспользоваться формулой Гаусса - Остроградского преобразуем это выражение следующим образом - внесём
. Для того чтобы воспользоваться формулой Гаусса - Остроградского преобразуем это выражение следующим образом - внесём 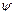 под знак дивергенции так:
под знак дивергенции так: 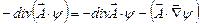 , тогда
, тогда 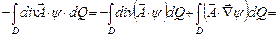 теперь применим формулу Гаусса - Остроградского
теперь применим формулу Гаусса - Остроградского 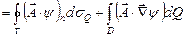 . Тогда наше скалярное произведение перепишется следующим образом:
. Тогда наше скалярное произведение перепишется следующим образом: 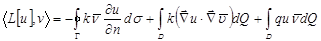 - первая формула Грина.
- первая формула Грина.
2. 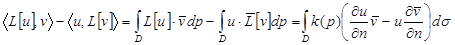 . – вторая формула Грина.
. – вторая формула Грина.
Теорема о единственности краевых задач:
Задача 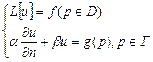 имеет единственное решение, если задача: имеет единственное решение, если задача: 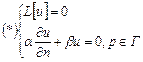 имеет лишь тривиальное решение имеет лишь тривиальное решение 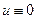 . . |
Доказательство: Воспользуемся первой формулой Грина:  , где
, где 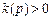 ,
, 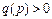 ,
, 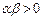
Рассмотрим все три типа краевых задач:
Первая краевая задача: 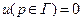
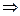
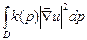 +
+ 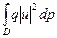 = 0 – т.е. сумма 2-х положительных величин, она равняется нулю тогда, когда
= 0 – т.е. сумма 2-х положительных величин, она равняется нулю тогда, когда 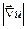 =0
=0 
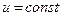 , и в силу
, и в силу 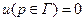 получаем, что
получаем, что 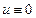 , ч.т.д.
, ч.т.д.
Третья краевая задача: из условия теоремы следует, что 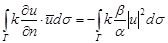 т.е. получаем сумму 3-х положительных величин, она равняется нулю тогда, когда
т.е. получаем сумму 3-х положительных величин, она равняется нулю тогда, когда 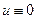 .
.
Вторая краевая задача: 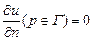
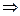
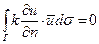
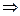
Рассмотрим два случая:
1) 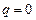 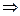 любая любая 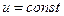 является решением - нет единственности. В качестве примера может служить следующая задача: является решением - нет единственности. В качестве примера может служить следующая задача: 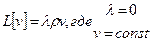 , ч.т.д. , ч.т.д. | 2)  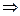 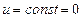 является единственным решением. является единственным решением. |
Физический смысл соотношений, получаемых с помощью формул Грина.
Рассмотрим задачу 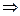
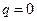 и
и 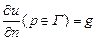 , u – решение
, u – решение 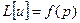 ,
,
И пусть 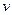 =1:
=1:
Используя 1-ую формулу Грина получаем ( 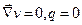 ,
, 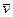 =1)
=1) 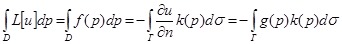 т.е. если решение рассмотренной задачи существует, то для f и g выполняется условие
т.е. если решение рассмотренной задачи существует, то для f и g выполняется условие 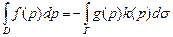 , и решение не существует, если оно не выполняется. Это соотношение имеет физический смысл
, и решение не существует, если оно не выполняется. Это соотношение имеет физический смысл  Тепло, выделяющееся источником внутри области, равно теплу, выходящему из области через границу в единицу времени.
Тепло, выделяющееся источником внутри области, равно теплу, выходящему из области через границу в единицу времени.
