Розв’язування систем лінійних рівнянь методом Гаусса

Метод Гаусса.

Розглянемо систему (1) т лінійних рівнянь із п невідомими у загальному випадку.

Метод Гаусса – метод послідовного виключення невідомих – полягає у тому, що за допомогою елементарних перетворень система рівнянь зводиться до рівносильної системи, з якої послідовно, починаючи з останніх (за номером) змінних, знаходять усі інші змінні.

Розглянемо систему рівнянь загального вигляду (1). Нехай для визначеності a₁₁¹0 (якщо a₁₁ =0, то можна переставити на перше місце ненульовий доданок або почат из другого рівняння). Помножимо перше рівняння на 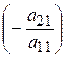і додамо до другого рівняння цієї системи. Дістанемо друге рівняння, в якому коефіцієнт при х₁ дорівнює нулю. Помноживши перше рівняння на 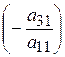і додавши до третього, дістанемо третє рівняння, яке також не містить х₁. Зробивши аналогічні дії над усіма іншими рівняннями, дістанемо систему еквівалентну (1):

,

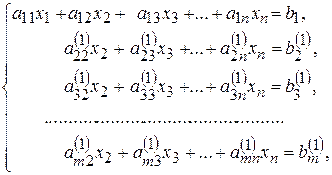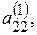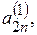
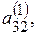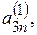
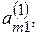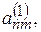
де …, …, …, …, 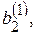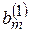- нові коефіцієнти й вільні члени. Індекс вгорі означає, що ці коефіцієнти отримані після першого кроку.

На другому кроці, припускаючи для визначеності, 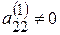і зберігаючи перші два рівняння останньої системи, перетворимо її так, щоб в усіх інших рівняннях коефіцієнти при х₂ перетворилися в нуль.

Продовжуючи процес послідовного виключення невідомих аналогічним чином доти, поки не дійдемо до останнього рядка, початкову систему (1) можна звести до однієї з трьох:

1) системи трикутного вигляду

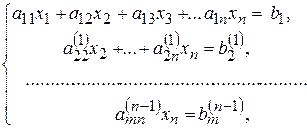
яка, як і початкова, має єдиний розв’язок, що шукається «з кінця»; якщо за допомогою елементарних перетворень матрицю коефіцієнтів квадратної системи можна привести до трикутної матриці (квадратна матриця, у якої на головній діагоналі стоять числа, відмінні від нуля, а під головною діагоналлю – нулі), то система сумісна та визначена;

2)

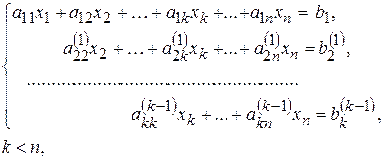
яка має нескінченну кількість розв’язків. Залишаємо члени з першими k невідомими на своїх місцях, а решту переносимо праворуч, надаючи їм довільних значень. Дістанемо систему k рівнянь із k невідомими трикутного вигляду. Вона легко розв’язується «з кінця», причому довільному наборові невідомих x_k+1, ¼, x_n відповідає набір x₁, x₂, ¼, x_k . Враховуючи, що наборів x_k+1, ¼, x_n існує безліч, дістанемо, що початкова система невизначена.

Отже, якщо при перетворенні розширеної матриці системи матриця коефіцієнтів приводиться до трапецієвидного вигляду, то система сумісна і є невизначеною.

Ті змінні, коефіцієнти при яких стоять на головній діагоналі трапецієвидної матриці (коефіцієнти відмінні від нуля), називаються базисними, інші невідомі називаються вільними.

Базисні невідомі єдиним способом виражаються через вільні невідомі.

Якщо вільним невідомим надані конкретні числові значення і через них виражені базисні невідомі, то отриманий розв’язок називається частинним розв’язком.

Якщо вільні невідомі виражені через параметри, то отримується розв’язок , який називається загальним розв’язком.

Якщо всім вільним невідомим надати нульових значень, то отриманий розв’язок називається базисним. Одну і ту ж систему, інколи, можна привести до різних наборів базисних невідомих.

Якщо отримані два різних набори базисних невідомих при різних способах знаходження розв’язку однієї і тої ж системи, то ці набори обов’язково містять одне й те ж число невідомих, яке називається рангом системи.

3) системи вигляду

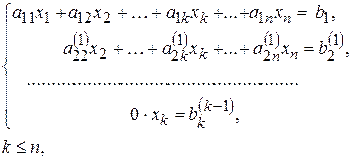
яка, очевидно, несумісна, оскільки жодні значення невідомих не можуть задовольнити її останнє рівняння.