Интерполяция на основе арифметических операций
ЧАСТЬ 2
ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ИЗОБРАЖЕНИЙ
Развитие средств связи, видеотехники, а также широкий спектр других тенденций, обусловленных прогрессом общества, создают гигантские объёмы графической информации. Известно, что хранение и обработка графической информации связаны с большими затратами компьютерных ресурсов. Используя кодирование изображений, мы можем существенно уменьшить размеры требуемой памяти. Но кодирование, например, видеофильма, состоящего из множества отдельных кадров, всё равно приведёт к очень большим затратам памяти (для комфортного восприятия человеческим глазом видеоряда необходима частота чередования 24 кадра в секунду). С другой стороны, кадры видеофильма образуют взаимосвязанную последовательную цепочку, поэтому процедуру сохранения и воспроизведения можно определённым образом оптимизировать. Обычно изображения, расположенные на соседних кадрах, отличаются несущественно. Актуальной задачей в таких условиях является задача о построении переходных, иначе говоря, интерполяционных изображений между двумя или несколькими заданными. Если запоминать не каждый кадр из последовательности, а лишь некоторые, и недостающие изображения восстанавливать по оставшимся, то размер необходимой информации о видеофильме сократится как минимум в 2 раза:
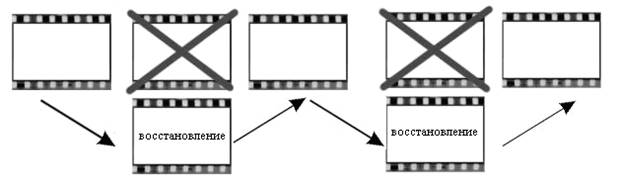
Рис. 1. Идея применения интерполяции к последовательности кадров
Интерполяция на основе арифметических операций
Задача построения (описания) переходных (интерполяционных) объектов между двумя заданными возникает в самых разных ситуациях. Рассмотрим простейший случай, в котором интерполируются векторы.
 Опишем семейство векторов
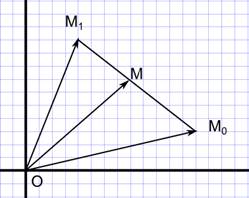
Опишем семейство векторов 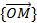 , которые являются переходными между двумя заданными векторами
, которые являются переходными между двумя заданными векторами 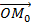 и
и 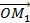 в смысле рис.2 (их конечные точки перемещаются по отрезку, соединяющему конечные точки заданных векторов). Выразим некоторый такой вектор
в смысле рис.2 (их конечные точки перемещаются по отрезку, соединяющему конечные точки заданных векторов). Выразим некоторый такой вектор 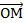 через
через 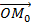 и
и 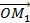 . По правилам действий с векторами получаем, что:
. По правилам действий с векторами получаем, что:
Рис.2. Интерполяция векторов 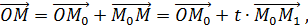
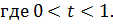 Представим вектор
Представим вектор 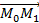 в виде разности векторов
в виде разности векторов 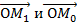 , тогда
, тогда
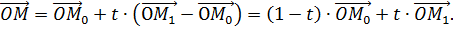
В итоге, приходим к формуле:

Данная формула описывает весь набор векторов, включая начальный и конечный.
 Отметим, что такая схема может быть применена для интерполяции любых объектов, на множестве которых определены операции сложения и умножения на положительное число (следовательно, в любом линейном пространстве), например, функций:
Отметим, что такая схема может быть применена для интерполяции любых объектов, на множестве которых определены операции сложения и умножения на положительное число (следовательно, в любом линейном пространстве), например, функций:
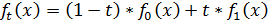 ,
,
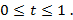
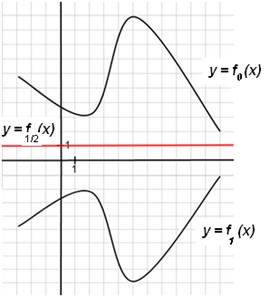
На рис.3 графически представлена процедура построения «средней», т.е. 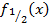 , функции между двумя заданными с
, функции между двумя заданными с
Рис.3. Интерполяция функций помощью данной формулы.
Арифметические операции над множествами в 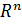
Итак, для реализации простейшего метода интерполяции объектов достаточно, чтобы для них имелись две основные арифметические операции. Такие операции над множествами точек были предложены в начале XX века немецким математиком Германом Минковским. Работая над вопросами по геометрии выпуклых тел, он ввел следующие понятия.
1. 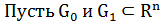 . Тогда сумма этих множеств (точек
. Тогда сумма этих множеств (точек 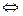 векторов) определяется как объединение всевозможных попарных сумм векторов из этих множеств:
векторов) определяется как объединение всевозможных попарных сумм векторов из этих множеств:
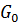 +
+ 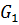
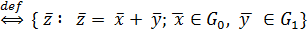
(к каждому из векторов, входящих в одно множество, нужно прибавить все векторы, составляющие другое) (рис. 4).
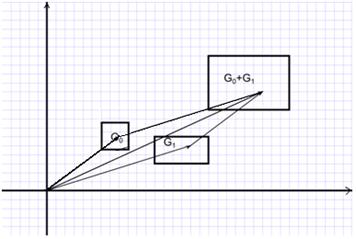
Рис. 4. Схема сложения множеств в R2
Отметим универсальный характер построения – формула применима к любой паре множеств (изображений). Однако фактические построения часто реализуются довольно сложно. На практике для сложения «простых» изображений удобно находить лишь границу (контуры) изображения, являющегося суммой, для чего достаточно «просуммировать» границы исходных.
Пример 1. Пусть 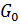 – квадрат, координаты вершин которого (0; 50), (0; -50), (-100; -50), (-100; 50),
– квадрат, координаты вершин которого (0; 50), (0; -50), (-100; -50), (-100; 50), 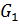 – квадрат с вершинами в точках (0; 0), (50; 50), (100; 0), (50; -50). Сложив множества
– квадрат с вершинами в точках (0; 0), (50; 50), (100; 0), (50; -50). Сложив множества 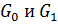 , получим восьмиугольник с вершинами (50; 100), (100; 50), (100; -50), (50; -100), (-50; -100), (-100; -50), (-100; 50), (-50; 100) ( рис.5):
, получим восьмиугольник с вершинами (50; 100), (100; 50), (100; -50), (50; -100), (-50; -100), (-100; -50), (-100; 50), (-50; 100) ( рис.5):
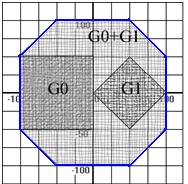
Рис. 5. Сумма двух квадратов
В дальнейшем нам понадобится такой результат.
Пример 2. Суммой круга 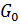 радиуса
радиуса 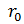 с центром в начале координат
с центром в начале координат 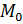 =
= 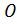 (0;0) и круга
(0;0) и круга 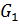 радиуса
радиуса 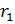 с центром в некоторой точке
с центром в некоторой точке 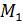 является круг с центром в точке
является круг с центром в точке 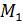 радиуса
радиуса 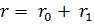 (рис.6).
(рис.6).
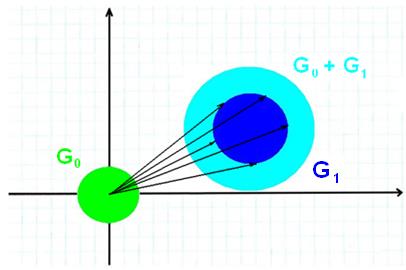
Рис. 6. Сумма двух кругов
Чтобы построить сумму данных множеств, к каждой точке границы круга 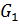 (к каждому вектору, проведённому из начала координат в некоторую точку границы
(к каждому вектору, проведённому из начала координат в некоторую точку границы 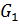 ) пририсуем окружность радиуса
) пририсуем окружность радиуса 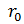 (прибавим всевозможные векторы, проведённые из начала координат к границе круга
(прибавим всевозможные векторы, проведённые из начала координат к границе круга 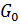 ). В итоге к кругу
). В итоге к кругу 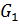 добавится кольцо ширины
добавится кольцо ширины 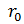 .
.
2. Умножение множества 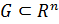 на число
на число 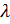 определяется как умножение всех векторов, составляющих данное множество, на это число (рис. 7):
определяется как умножение всех векторов, составляющих данное множество, на это число (рис. 7):
λ * 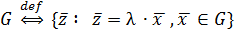 .
.
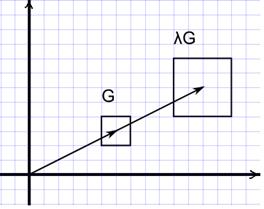
Рис.7. Схема умножения в R2 множества 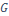 на число
на число 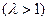
Пример 3. Пусть 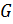 – прямоугольный треугольник, вершины которого имеют координаты (25; 25), (25; 75), (75; 25). Тогда
– прямоугольный треугольник, вершины которого имеют координаты (25; 25), (25; 75), (75; 25). Тогда 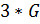 – прямоугольный треугольник с вершинами (75; 75), (75; 225), (225; 75) (рис.8):
– прямоугольный треугольник с вершинами (75; 75), (75; 225), (225; 75) (рис.8):
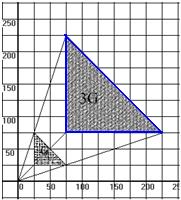
Рис. 8. Умножение треугольника на число 3.
Отметим основные свойства введённых операций:
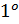 )
) 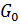 +
+ 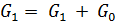
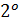 ) (
) ( 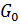 +
+ 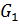 ) +
) + 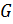 =
= 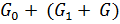
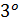 ) λ *(µ ∗
) λ *(µ ∗ 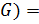 (λµ)∗
(λµ)∗ 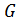
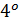 ) λ *(
) λ *( 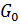 +
+ 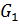 ) = λ∗
) = λ∗ 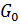 + λ∗
+ λ∗