Раздел 1. Линейная и векторная алгебра

1. Определение матрицы размера 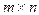. Определение матрицы n-го порядка. Вектор-строка, вектор-столбец. Главная диагональ матрицы. Равные матрицы; нулевая матрица.

2. Сумма матриц, произведение матрицы на число. Определение противоположной матрицы. Свойства сложения матриц и умножения их на число.

3. Определение транспонированной матрицы. Замечания о размерности транспонированной матрицы и о транспонированной матрице по отношению к транспонированной.

4. Определение произведения матриц. Условия согласования при умножении. Определение единичной матрицы. Свойства произведения.

5. Определение определителя 2-го порядка. Определение определителя
3-го порядка. Минор некоторого элемента 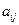определителя 3-го порядка. Алгебраическое дополнение 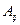элемента 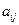.Разложение определителя по строке, столбцу.

6. Разложение определителя по строке, столбцу.

7. Связь между определителями исходной и транспонированной матриц.

8. Перемена местами 2-х строк определителя. Определитель с совпадающими строками.

9. Определитель со строкой, умноженной на число и со строкой, составленной из сумм чисел.

10. Определитель со строкой, равной линейной комбинации других строк. Возможность прибавления к строке определителя другой строки, умноженной на число.

11. Определитель с нулевой строкой. Определитель произведения матриц.

12. Определение обратной матрицы. Единственность обратной матрицы; вычисление обратной матрицы по отношению к обратной.

13. Обратная матрица от произведения матриц.

14. Матрица алгебраических дополнений. Присоединенная матрица. Теорема о существовании и виде обратной матрицы (формула обратной матрицы). Техника вычисления обратной матрицы.

15. Линейные системы m уравнений с n неизвестными. Матричная запись системы линейных алгебраических уравнений (СЛАУ). Решение СЛАУ.

16. Определение треугольной матрицы. Расширенная матрица СЛАУ Решение СЛАУ методом Гаусса.

17. Линейные системы n уравнений с n неизвестными. Главный и вспомогательные определители СЛАУ размера 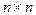. Формулы Крамера. Обратная теорема и ее следствие.

18. Матричный метод решения СЛАУ размера .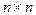

19. Понятие вектора в Rⁿ. Линейная комбинация векторов в Rⁿ. Линейно независимые и линейно зависимые системы векторов в Rⁿ. Критерий линейной зависимости векторов. Системы векторов, содержащие нулевой вектор.

20. Система векторов, содержащая линейно зависимую подсистему. Подсистемы линейно независимых систем векторов. Критерий линейной независимости системы n векторов в Rⁿ.

21. Базисность системы векторов в Rⁿ. Координаты вектора относительно данного базиса. Естественный базис в Rⁿ и, в частности, в R³. Практическое обоснование базисности системы векторов и нахождение координат вектора относительно этого базиса.

22. Векторы в R² и R³ как направленные отрезки.

23. Определение скалярного произведения векторов в Rⁿ. Свойства скалярного произведения. Вычисление длины вектора и угла между векторами в R² и R³.

24. Определение нормы вектора и угла между векторами в Rⁿ. Определение проекции вектора на вектор в Rⁿ. Техника вычисления длин, углов и проекций. Свойства нормы вектора.

25. Определение ортогональных векторов в Rⁿ. Определение единичного вектора. Определение ортонормированного базиса в Rⁿ. Нормировка вектора.

26. Определение векторного произведения векторов. Техника вычисления площадей.

27. Свойства векторного произведения. Вычисление векторных произведений. Выражение векторного произведения через координаты векторов.

28. Определение смешанного произведения векторов. Вычисление смешанного произведения векторов через их координаты. Свойства смешанного произведения.

29. Геометрический смысл смешанного произведения. Техника вычисления объемов. Задача о принадлежности четырех точек одной плоскости.