Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами.
Будем искать частные решения уравнения (2) в виде
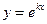 ,
,
где 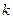 - некоторое произвольное число.
- некоторое произвольное число.
Подстановка решения в таком виде в уравнение (2) приводит к характеристическому уравнению, позволяющему найти число 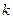
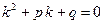 . (3)
. (3)
Поскольку уравнение (3) является квадратным уравнением, возможны различные частные случаи.
Случай 1. Корни 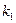 и
и 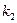 уравнения (3) действительные и различные:
уравнения (3) действительные и различные: 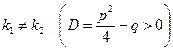 .
.
В этом случае частными решениями уравнения (2), образующими фундаментальную систему, будут функции 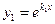 и
и 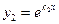 , а его общим решением будет функция
, а его общим решением будет функция
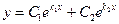 .
.
Случай 2. Корни 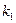 и
и 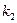 уравнения (3) действительные и равные:
уравнения (3) действительные и равные: 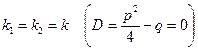 .
.
В этом случае в качестве фундаментальных решений уравнения (2) следует взять функции 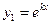 и
и 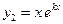 , общим же решением будет функция
, общим же решением будет функция
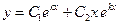 .
.
Случай 3. Корни 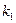 и
и 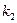 уравнения (3) комплексные:
уравнения (3) комплексные: 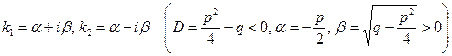 .
.
В этом случае частными решениями уравнения (2), образующими фундаментальную систему, будут функции комплексного переменного 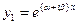 и
и 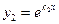 , а его общим решением будет функция
, а его общим решением будет функция
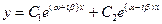 .
.
Используя формулы Эйлера, можно перейти к фундаментальной системе функций действительного переменного
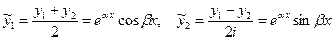 .
.
Тогда общее решение уравнения (2) запишется в виде
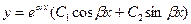 .
.
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами (выбор частных решений для некоторых функций в правой части уравнений, метод вариации постоянных).
I. Определение. Линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение
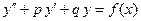 , (1)
, (1)
где 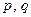 - постоянные,
- постоянные, 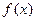 - некоторая функция.
- некоторая функция.
II.Общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами можно получить как сумму общего решения однородного уравнения и какого-либо решения неоднородного уравнения, т.е.
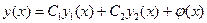 ,
,
где 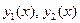 - фундаментальная система решений однородного уравнения.
- фундаментальная система решений однородного уравнения.
В некоторых специальных случаях есть некоторые правила поиска частного решения 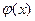 (метод неопределенных коэффициентов).
(метод неопределенных коэффициентов).
Случай 1. 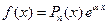 , где
, где 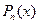 - многочлен степени
- многочлен степени 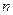 .
.
А. Если 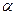 не является корнем характеристического уравнения
не является корнем характеристического уравнения
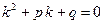 , (2)
, (2)
то частное решение 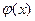 следует искать в виде
следует искать в виде
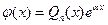 ,
,
где 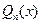 - многочлен n-ой степени с произвольными коэффициентами.
- многочлен n-ой степени с произвольными коэффициентами.
Б. Если 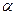 - корень уравнения (2) кратности
- корень уравнения (2) кратности 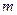 , то частное решение
, то частное решение 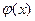 ищут в виде
ищут в виде 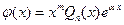 .
.
Случай 2. 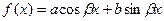 .
.
А. Если числа 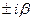 не являются корнями характеристического уравнения (2), то частное решение
не являются корнями характеристического уравнения (2), то частное решение 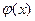 следует искать в виде
следует искать в виде
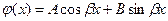 ,
,
где 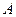 и
и 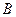 - произвольные постоянные.
- произвольные постоянные.
Б. Если числа 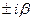 являются корнями характеристического уравнения (2), то частное решение
являются корнями характеристического уравнения (2), то частное решение 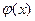 ищут в виде
ищут в виде
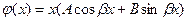 .
.
Замечание. В случаях 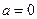 или
или 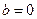 частное решение по-прежнему следует искать в указанном полном виде.
частное решение по-прежнему следует искать в указанном полном виде.
Случай 3. 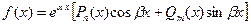 , где
, где 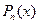 и
и 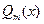 - многочлены степени m и n, соответственно.
- многочлены степени m и n, соответственно.
А. Если 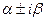 не являются корнями характеристического уравнения (2), то частное решение
не являются корнями характеристического уравнения (2), то частное решение 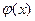 следует искать в виде
следует искать в виде
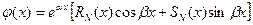 ,
,
где 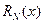 и
и 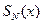 - многочлены с произвольными коэффициентами степени
- многочлены с произвольными коэффициентами степени 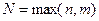 .
.
Б. Если 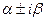 являются корнями характеристического уравнения (2), то частное решение
являются корнями характеристического уравнения (2), то частное решение 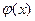 ищут в виде
ищут в виде
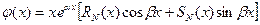 .
.
Для нахождения частного решения уравнения (1) в общем случае можно воспользоваться методом вариации постоянных (методом Лагранжа).
Рассмотрим общее решение однородного уравнения
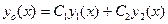 .
.
Частное решение неоднородного уравнения (1) ищется в виде
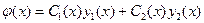 ,
,
где 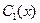 и
и 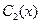 - дифференцируемые функции, которые находятся путем решения системы дифференциальных уравнений
- дифференцируемые функции, которые находятся путем решения системы дифференциальных уравнений
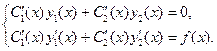
Замечание. Пусть мы имеем уравнение 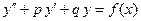 , где
, где 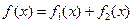 . Если функции
. Если функции 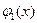 и
и 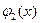 являются решениями соответственно уравнений
являются решениями соответственно уравнений 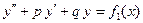 и
и 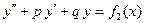 , то функция
, то функция 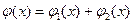 - решение уравнения
- решение уравнения 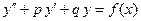 .
.
