ЗАНЯТИЕ 5. Уравнения первого порядка, не разрешенные относительно производной.
| Ауд. | Л-3 | гл.10: № 114, 116, 118, 120, 122,124. |
☺ ☻ ☺
Пример 1–114: Найти общее решение уравнения: y=(y′)2+4(y′)3 в параметрической форме.
Решение:
a0. Форма записи уравнения имеет вид: y=φ(y′).
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p. Тогда исходное уравнение принимает вид: y=φ(p)=p2+4p3.
a2. Учитывая: y′= 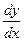 , запишем dy=φ′(p)dp, где: φ′(p)=2p+12p2. Получаем уравнение для нахождения x: dx=
, запишем dy=φ′(p)dp, где: φ′(p)=2p+12p2. Получаем уравнение для нахождения x: dx= 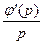 dp=(2+12p)dp.
dp=(2+12p)dp.
a3. Запишем выражение для x: x= 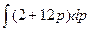 +С=2p+6p2+С.
+С=2p+6p2+С.
a3. Составляем систему: 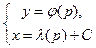 , или
, или 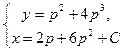 – параметрическое решение.
– параметрическое решение.
a4. Пробуем исключить из системы параметр p → F(x,y,C)=0 – общий интеграл. В нашем случае «можно не пробовать»!
Ответ: 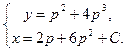 – общее решение в параметрической форме. Решение y=0 – особое.
– общее решение в параметрической форме. Решение y=0 – особое.
Пример 2–116: Найти общее решение уравнения: y=(y′–1)ey′ в параметрической форме.
Решение:
a0. Форма записи уравнения имеет вид: y=φ(y′).
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p → исходное уравнение принимает вид: y=φ(p) =(p–1)ep.
a2. Учитывая: y′= 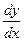 , запишем dy=φ′(p)dp, где: φ′(p)=pep. Получаем уравнение для нахождения x: dx=
, запишем dy=φ′(p)dp, где: φ′(p)=pep. Получаем уравнение для нахождения x: dx= 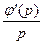 dp=epdp.
dp=epdp.
a3. Запишем выражение для x: x= 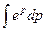 +С=ep +С.
+С=ep +С.
a4. Составляем систему: 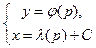 , или
, или 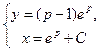 – параметрическое решение.
– параметрическое решение.
a5. Пробуем исключить из системы параметр p → F(x,y,C)=0 – общий интеграл. В нашем случае «можно не пробовать»!
Ответ: 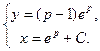 – общее решение в параметрической форме.
– общее решение в параметрической форме.
Пример 3–118: Найти общее решение уравнения: x=y′3–y′+2 в параметрической форме.
Решение:
a0. Форма записи уравнения имеет вид: x=φ(y′).
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p. Тогда исходное уравнение принимает вид: x=φ(p)=p3–p+2.
a2. Учитывая: y′= 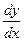 , или dy=pdx, запишем dx=φ′(p)dp, где: φ′(p)=3p2–1. Получаем уравнение для нахождения y: dy=pφ′(p)dp=(3p3–p)dp.
, или dy=pdx, запишем dx=φ′(p)dp, где: φ′(p)=3p2–1. Получаем уравнение для нахождения y: dy=pφ′(p)dp=(3p3–p)dp.
a3. Запишем выражение для y: y= 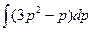 +С=
+С= 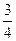 p4–
p4– 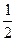 p2+С=μ(p)+С.
p2+С=μ(p)+С.
a4. Составляем систему: 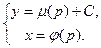 , или
, или 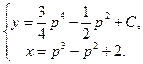
a5. Пробуем исключить из системы параметр p → F(x,y,C)=0 – общий интеграл. В нашем случае «можно не пробовать»!
Ответ: 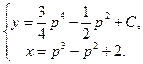 – общее решение в параметрической форме.
– общее решение в параметрической форме.
Пример 4–120: Найти общее решение уравнения: x=2y′–lny′ в параметрической форме.
Решение:
a0. Форма записи уравнения имеет вид: x=φ(y′).
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p. Тогда исходное уравнение принимает вид: x=φ(p)=2p–lnp.
a2. Учитывая: y′= 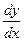 , или dy=pdx, запишем dx=φ′(p)dp, где: φ′(p)=2–
, или dy=pdx, запишем dx=φ′(p)dp, где: φ′(p)=2– 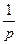 . Получаем уравнение для нахождения y: dy=pφ′(p)dp=(2p–1)dp.
. Получаем уравнение для нахождения y: dy=pφ′(p)dp=(2p–1)dp.
a3. Запишем выражение для y: y= 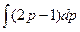 +С=p2–p+С=μ(p)+С.
+С=p2–p+С=μ(p)+С.
a3. Составляем систему: 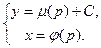 , или
, или 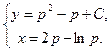
a4. Пробуем исключить из системы параметр p → F(x,y,C)=0 – общий интеграл. В нашем случае «можно не пробовать»!
Ответ: 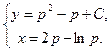 – общее решение в параметрической форме.
– общее решение в параметрической форме.
Пример 5–122: Найти решение уравнения Лагранжа: y=x 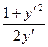 , применяя метод введения параметра.
, применяя метод введения параметра.
Решение:
a0. Форма записи уравнения имеет вид: y=φ(y′)∙x+ψ(y′), где φ(y′)= 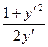 и ψ(y′)=0.
и ψ(y′)=0.
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p → исходное уравнение принимает вид: y=φ(p)∙x+ψ(p)=x∙ 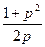 .
.
a2. Дифференцируя последнее по x имеем: p–φ(p)=[x∙φ′(p)+ψ′(p)] 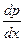 .
.
a3. Запишем равенство: p–φ(p)= 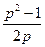 =0, его решения: p0=–1 и p0=1. Учитывая p0 ≡φ(p0), запишем: а) для p0=–1: y=φ(p0)∙x+ψ(p0) → y=–1∙x+0=–x;
=0, его решения: p0=–1 и p0=1. Учитывая p0 ≡φ(p0), запишем: а) для p0=–1: y=φ(p0)∙x+ψ(p0) → y=–1∙x+0=–x;
б) для p0=1: y=φ(p0)∙x+ψ(p0) → y=1∙x+0= х.
Пока не получено общее решение уравнения, мы не можем сказать, будут эти решения особыми, или нет.
a4. Пусть теперь p–φ(p) ≠ 0. Запишем уравнение для вычисления x:
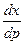 –x
–x 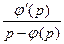 =
= 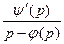 , или
, или 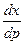 – x
– x 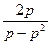 =
= 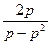 , или
, или 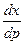 = –(x+1)
= –(x+1) 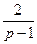 .
.
a5. Теперь p–φ(p)≠0. Для нахождения x решим: 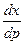 –x
–x 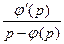 =
= 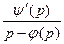 – линейное уравнение. В нашем случае:
– линейное уравнение. В нашем случае: 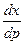 –x
–x 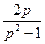 ∙
∙ 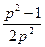 =0, или
=0, или 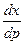 = x
= x 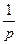 : уравнение с разделяющимися переменными → p = Cx.
: уравнение с разделяющимися переменными → p = Cx.
a6. Cистема: 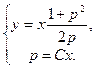 легко приводится к виду → y=
легко приводится к виду → y= 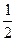 Cx2+
Cx2+ 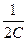 – общий интеграл заданного уравнения.
– общий интеграл заданного уравнения.
Ответ: y= 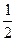 Cx2+
Cx2+ 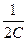 – общий интеграл заданного уравнения. Особое решение: y = ±x.
– общий интеграл заданного уравнения. Особое решение: y = ±x.
Пример 6–124: Найти решение уравнения Лагранжа: y=x(y′)2+(y′)3, применяя метод введения параметра.
Решение:
a0. Форма записи уравнения имеет вид: y=φ(y′)∙x+ψ(y′), где φ(y′)=(y′)2 и ψ(y′)=(y′)3.
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p → исходное уравнение принимает вид: y=φ(p)∙x+ψ(p)=x∙p2+p3.
a2. Дифференцируя последнее по x имеем: p–φ(p)=[x∙φ′(p)+ψ′(p)] 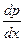 . В нашем случае это равенство: p–p2=[x∙2p+3p]
. В нашем случае это равенство: p–p2=[x∙2p+3p] 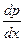 .
.
a3. Запишем равенство: p–φ(p)=p–p2=0, его решения: p0=0 и p0=1. Учитывая p0 ≡φ(p0), запишем: а) для p0=0: y=φ(p0)∙x+ψ(p0) → y=0∙x+0=0;
б) для p0=1: y=φ(p0)∙x+ψ(p0) → y=1∙x+1= х+1.
Пока не получено общее решение уравнения, мы не можем сказать, будут эти решения особыми, или нет.
a4. Теперь p–φ(p)≠0. Для нахождения x решим: 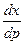 –x
–x 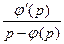 =
= 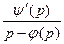 – линейное уравнение. В нашем случае:
– линейное уравнение. В нашем случае: 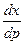 –x
–x 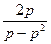 =
= 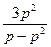 =0, или
=0, или 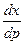 +
+ 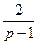 x=–
x=– 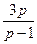 .
.
Данное линейное уравнение решаем, применяя общий алгоритм:
a5. Решение уравнения ищем в виде функции: x=u∙v.
a6. Вычислим: – 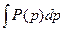 =–
=– 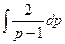 =–2ln|p–1|, и запишем: u=
=–2ln|p–1|, и запишем: u= 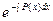 , то есть u =
, то есть u = 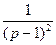 .
.
a8. Вычислим функцию v: v = 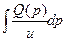 +С= –
+С= – 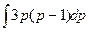 +С =
+С = 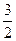 p2– p3+С.
p2– p3+С.
a9. Запишем общее решение линейного уравнения для x:
x=u∙v= 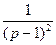 ∙
∙ 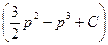 =
= 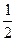 ∙
∙ 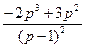 +
+ 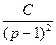 .
.
Замечание: если в последнем выражении в первой дроби выполнить операцию «выделение целой части», то выражение существенно упростится: x= –p– 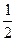 +
+ 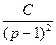 .
.
a10. Если в выражение: y=x∙p2+p3 подставить выражение для x, то для y получим выражение через параметр p: y= – 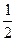 p2+
p2+ 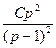 .
.
a11. Составляем систему: 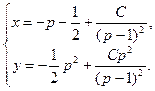 Это решение уравнения в параметрической форме.
Это решение уравнения в параметрической форме.
a12. Пробуем исключить из системы параметр p → F(x,y,C)=0 – общий интеграл. В нашем случае «можно не пробовать»!
Ответ: 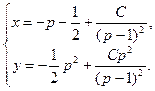 – решение уравнения в параметрической форме. Особые решения: y=0; y =x+1.
– решение уравнения в параметрической форме. Особые решения: y=0; y =x+1.
* * * * * * * * * *
Домашнее задание
| Дома | Л-3 | гл.10: № 115, 117, 119, 121, 123,125, 177. |
Пример 1–115: Найти общее решение уравнения: y=y′ 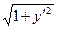 в параметрической форме.
в параметрической форме.
Решение:
a0. Форма записи уравнения имеет вид: y=φ(y′).
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p. Тогда исходное уравнение принимает вид: y=φ(p)=p 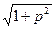 .
.
a2. Учитывая: y′= 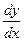 , запишем dy=φ′(p)dp, где: φ′(p)=
, запишем dy=φ′(p)dp, где: φ′(p)= 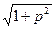 +
+ 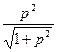 =
= 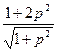 . Получаем уравнение для нахождения x: dx=
. Получаем уравнение для нахождения x: dx= 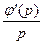 dp=(
dp=( 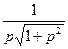 +
+ 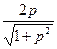 )dp.
)dp.
a3. Запишем выражение для x: x= 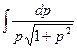 +
+ 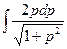 +С=J1+J2+С. Вычислим интегралы: J1=
+С=J1+J2+С. Вычислим интегралы: J1= 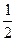
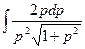 =[Замена:p2=t]=
=[Замена:p2=t]= 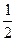
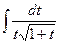 =[Замена:
=[Замена: 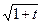 =u]=
=u]= 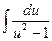 =lnp–ln(1+
=lnp–ln(1+ 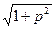 ),
),
J2=2 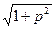 . Окончательно: x=2
. Окончательно: x=2 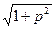 +lnp–ln(1+
+lnp–ln(1+ 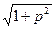 )+С.
)+С.
a3. Составляем систему: 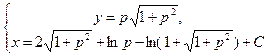 – общее решение уравнения в параметрической форме.
– общее решение уравнения в параметрической форме.
a4. Пробуем исключить из системы параметр p → F(x,y,C)=0 – общий интеграл. В нашем случае «можно не пробовать»!
Ответ: 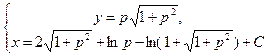 – общее решение в параметрической форме. Решение y=0 – особое.
– общее решение в параметрической форме. Решение y=0 – особое.
Пример 2–117: Найти общее решение уравнения: y= 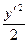 +2xy′+x2.
+2xy′+x2.
Решение:
a0. Форма записи уравнения имеет вид: y=F(x,y′): не отвечает ни одной из рассмотренных.
Данное уравнение решаем, применяя алгоритм введения параметра:
a1. Примем y′=p → исходное уравнение принимает вид: y= 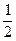 p2+2xp+x2.
p2+2xp+x2.
a2. Учитывая, что p есть функция от x, продифференцируем выражение для y по переменной x, сразу заменяя y′=p: p=(p+2x) 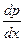 +2p+2x, или: (p+2x)(
+2p+2x, или: (p+2x)( 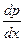 +1)=0. (2.1)
+1)=0. (2.1)
a3. Из равенства (2.1) получаем:
▪ p= –2x → dy= –2xdx → y= –x2+С. Подставив функцию y= –x2+С в исходное уравнение, получим требование С=0. Итак, y= –x2 есть решение заданного ДУ.
▪ dp= –dx → p= –x+С → dy=(С–x)→ y=Сx– 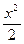 . Подставив функцию y= Сx–
. Подставив функцию y= Сx– 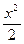 в исходное уравнение, получим: y=Сx+
в исходное уравнение, получим: y=Сx+ 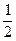 (С2–x2).
(С2–x2).
a4. Итак, получено общее решение: y=Сx+ 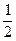 (С2–x2) – семейство парабол. Частное решение: y= –x2 не может быть получено из общего и потому является особым.
(С2–x2) – семейство парабол. Частное решение: y= –x2 не может быть получено из общего и потому является особым.
Ответ: y=Сx+ 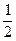 (С2–x2) – общее решение уравнения. Решение y= –x2 – особое решение ДУ.
(С2–x2) – общее решение уравнения. Решение y= –x2 – особое решение ДУ.
Пример 3–119: Найти общее решение уравнения: x=y′cosy′.
Решение:
a0. Форма записи уравнения имеет вид: x=φ(y′).
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p. Тогда исходное уравнение принимает вид: x==φ(p)=pcosp.
a2. Учитывая: y′= 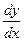 , или dy=pdx, запишем dx=φ′(p)dp, где: φ′(p)=cosp–psinp. Получаем уравнение для нахождения y: dy=pφ′(p)dp=p(cosp–psinp)dp.
, или dy=pdx, запишем dx=φ′(p)dp, где: φ′(p)=cosp–psinp. Получаем уравнение для нахождения y: dy=pφ′(p)dp=p(cosp–psinp)dp.
a3. Вычислим: y= 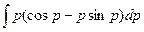 +С=
+С= 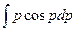 –
– 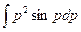 =J1–J2+С. Интеграл J1 «табличный»: J1=psinp+cosp. Применяя к J2 «интегрирование по частям», получим выражение: J2= –p2cosp+2
=J1–J2+С. Интеграл J1 «табличный»: J1=psinp+cosp. Применяя к J2 «интегрирование по частям», получим выражение: J2= –p2cosp+2 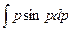 = –p2cosp+2J1. Окончательно:
= –p2cosp+2J1. Окончательно:
y= p2cosp–psinp–cosp +С.
a4. Система уравнений: 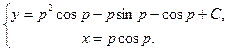 определяет общее решение исходного уравнения в параметрической форме.
определяет общее решение исходного уравнения в параметрической форме.
Ответ: 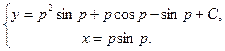 – общее решение в параметрической форме.
– общее решение в параметрической форме.
Пример 4–121: Найти общее решение уравнения: x= 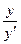 +
+ 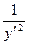 в параметрической форме.
в параметрической форме.
Решение:
a0. Форма записи уравнения имеет вид: x=φ(y,y′). Если заменить y′= 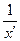 , то получится уравнение: x= x′∙ y + x′2 . Это уравнение Клеро! Будем считать, что мы этого не заметили, и решим его по общей схеме для уравнений, не разрешенных относительно производной.
, то получится уравнение: x= x′∙ y + x′2 . Это уравнение Клеро! Будем считать, что мы этого не заметили, и решим его по общей схеме для уравнений, не разрешенных относительно производной.
Применим общий алгоритм введения параметра:
a1. Примем y′=p. Тогда исходное уравнение принимает вид: x=φ(y,p)= 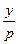 +
+ 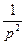 , причем p является функцией от y (!) через посредство x.
, причем p является функцией от y (!) через посредство x.
a2. Учитывая: y′= 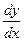 , продифференцируем равенство x=φ(y,p) по y:
, продифференцируем равенство x=φ(y,p) по y:
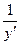 =
= 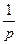 –
– 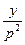
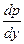 –2
–2 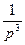
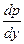 →
→ 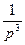 (2+py)
(2+py) 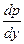 =0.
=0.
a3. Из последнего получим продолжение:
а) 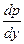 =0 → p=С → общее решение: x=Сy+С2;
=0 → p=С → общее решение: x=Сy+С2;
б) 2+py =0 → 2dx+ydy =0 → 4x+y2=0 – особое решение (из общего решения не получается ни при каком значении С!).
Ответ: x=Сy+С2 – общее решение, 4x+y2=0 – особое решение.
Пример 5–123: Найти решение уравнения Лагранжа: y=2xy′ + 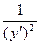 , применяя метод введения параметра.
, применяя метод введения параметра.
Решение:
a0. Форма записи уравнения имеет вид: y=φ(y′)∙x+ψ(y′), где φ(y′)=2y′ и ψ(y′)= 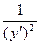 .
.
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p → исходное уравнение принимает вид: y=φ(p)∙x+ψ(p)= 2xp + 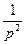 .
.
a2. Дифференцируя последнее по x имеем: p–φ(p)=[x∙φ′(p)+ψ′(p)] 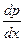 .
.
a3. Запишем равенство: p–φ(p)=p–2p=–p=0, его решение: p0=0. Учитывая p0 ≡φ(p0), запишем: y=φ(p0)∙x+ψ(p0), что невозможно, так как ψ(p0) не существует.
a5. Теперь p–φ(p)≠0. Для нахождения x решим: 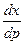 –x
–x 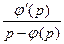 =
= 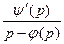 – линейное уравнение. В нашем случае:
– линейное уравнение. В нашем случае: 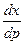 –x
–x 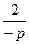 =
= 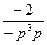 , или
, или 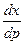 +
+ 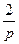 x=
x= 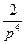 : линейное уравнение.
: линейное уравнение.
Данное линейное уравнение решаем, применяя общий алгоритм:
a5. Решение уравнения ищем в виде функции: x=u∙v.
a6. Вычислим: – 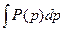 =–
=– 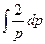 =–2ln|p|, и запишем: u=
=–2ln|p|, и запишем: u= 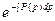 , то есть u =
, то есть u = 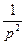 .
.
a8. Вычислим функцию v: v = 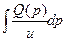 +С= 2
+С= 2 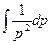 +С = –
+С = – 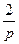 +С.
+С.
a9. Запишем общее решение линейного уравнения для x:
x=u∙v= 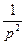 ∙
∙ 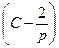 =
= 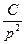 –
– 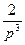 .
.
a10. Если в выражение: y=2xp + 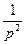 подставить найденное выражение для x, то для y получим выражение через параметр p: y=
подставить найденное выражение для x, то для y получим выражение через параметр p: y= 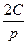 –
– 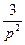 .
.
a11. Составляем систему: 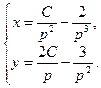 Это решение уравнения в параметрической форме.
Это решение уравнения в параметрической форме.
a12. Пробуем исключить из системы параметр p → F(x,y,C)=0 – общий интеграл. В нашем случае «можно не пробовать»!
Ответ: 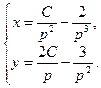 – решение уравнения в параметрической форме.
– решение уравнения в параметрической форме.
Пример 6–125: Найти решение уравнения Лагранжа: y= 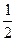 y′x+
y′x+ 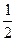 y′lny′, применяя метод введения параметра.
y′lny′, применяя метод введения параметра.
Решение:
a0. Форма записи уравнения имеет вид: y=φ(y′)∙x+ψ(y′), где φ(y′)= 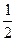 y′ и ψ(y′)=
y′ и ψ(y′)= 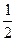 y′lny′.
y′lny′.
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p → исходное уравнение принимает вид: y=φ(p)∙x+ψ(p)=x∙ 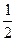 p+
p+ 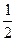 plnp.
plnp.
a2. Дифференцируя последнее по x имеем: p–φ(p)=[x∙φ′(p)+ψ′(p)] 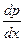 . В нашем случае это равенство: p–
. В нашем случае это равенство: p– 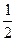 p =
p = 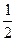 [x∙1+lnp+1]
[x∙1+lnp+1] 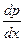 , или p=[x+lnp+1]
, или p=[x+lnp+1] 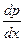 .
.
a3. Запишем равенство: p–φ(p)=p=0, его решения: p0=0. запишем: y=φ(p0)∙x+ψ(p0), что невозможно, так как ψ(p0) не существует.
a4. Теперь p–φ(p)≠0. Для нахождения x решим: 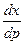 –x
–x 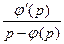 =
= 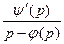 – линейное уравнение. В нашем случае:
– линейное уравнение. В нашем случае: 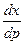 –x
–x 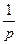 =
= 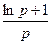 =0.
=0.
Данное линейное уравнение решаем, применяя общий алгоритм:
a5. Решение уравнения ищем в виде функции: x=u∙v.
a6. Вычислим: – 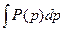 =
= 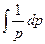 =ln|p|, и запишем: u=
=ln|p|, и запишем: u= 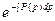 , то есть u =p.
, то есть u =p.
a8. Вычислим функцию v: v = 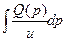 +С=
+С= 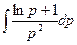 +С =–
+С =– 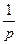 (lnp+2)+С.
(lnp+2)+С.
a9. Запишем общее решение линейного уравнения для x:
x=u∙v=p ∙ 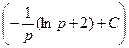 =Cp–lnp–2.
=Cp–lnp–2.
a10. Если в выражение: y=x∙ 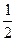 p+
p+ 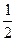 plnp подставить выражение для x, то для y получим выражение через параметр p: y=
plnp подставить выражение для x, то для y получим выражение через параметр p: y= 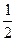 Cp2–p.
Cp2–p.
a11. Составляем систему: 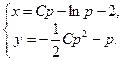 Это решение уравнения в параметрической форме.
Это решение уравнения в параметрической форме.
a12. Пробуем исключить из системы параметр p → F(x,y,C)=0 – общий интеграл. В нашем случае «можно не пробовать»!
Ответ: 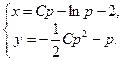 – решение уравнения в параметрической форме.
– решение уравнения в параметрической форме.
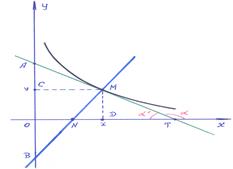
Пример 5–177: Найти уравнение кривой, проходящей через точку (3,1), если длина отрезка оси абсцисс, отсекаемого любой ее касательной на оси ординат, равна поднормали.
 Решение:
Решение:
В Примере 1–19 получены выражения для указанных в условии: А=(0,y–y′х) и ND =(–yy′,0).
Замечание: В условии задачи допущена некорректность. Необходимо уточнить: ОА=(0,y–y′х), |ОА|=|y–y′х|, |ND|=|yy′|, тогда условие задачи: |ОА|=|ND|.
Необходимо рассмотреть два случая:
▪ Случай-1: y–y′х = –yy′; (1)
▪ Случай-2: y–y′х = yy′. (2)
Случай-1.
a0. Из условия (1) запишем: y= 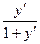 ∙х. Форма записи уравнения имеет вид уравнения Лагранжа: y=φ(y′)∙x+ψ(y′), где φ(y′)=
∙х. Форма записи уравнения имеет вид уравнения Лагранжа: y=φ(y′)∙x+ψ(y′), где φ(y′)= 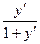 и ψ(y′)=0.
и ψ(y′)=0.
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p → исходное уравнение принимает вид: y=φ(p)∙x+ψ(p)=x∙ 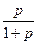 .
.
a2. Дифференцируя последнее по x имеем: p–φ(p)=[x∙φ′(p)+ψ′(p)] 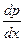 .
.
a3. Запишем равенство: p–φ(p)= 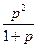 =0, его решения: p0=0. Учитывая p0 ≡φ(p0), запишем: y=φ(p0)∙x+ψ(p0) → y= 0∙x+0= 0. Пока не получено общее решение уравнения, мы не можем сказать, будет ли это решение особыми.
=0, его решения: p0=0. Учитывая p0 ≡φ(p0), запишем: y=φ(p0)∙x+ψ(p0) → y= 0∙x+0= 0. Пока не получено общее решение уравнения, мы не можем сказать, будет ли это решение особыми.
a4. Пусть теперь p–φ(p) ≠ 0. Уравнение для вычисления x: 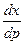 –x
–x 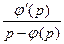 =
= 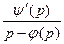 , или
, или 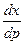 – x
– x 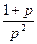 ∙
∙ 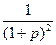 =0, или
=0, или 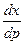 = x
= x 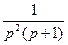 уравнение с разделяющимися переменными.
уравнение с разделяющимися переменными.
a5. Интегрируем уравнение (предварительно разложив дробь 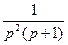 : осуществляется по общей формуле разложения, используемой при интегрировании рациональных дробей: см. математический анализ!):
: осуществляется по общей формуле разложения, используемой при интегрировании рациональных дробей: см. математический анализ!): 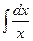 =
= 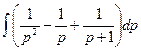 = –
= – 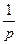 –ln
–ln 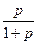 , или в виде:
, или в виде:
ln 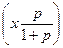 = –
= – 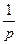 +C.
+C.
a6. Если учесть исходное: y=x∙ 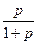 , то –
, то – 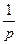 = –
= – 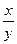 +1. Тогда lny= –
+1. Тогда lny= – 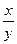 –1+C, или
–1+C, или 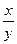 =C–lny – общее решение исходного уравнения.
=C–lny – общее решение исходного уравнения.
a7. Учитывая начальные условия, получим: 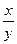 =3–lny – частное решение, для C=3.
=3–lny – частное решение, для C=3.
Случай-2.
a0. Из условия (1) запишем: y= 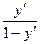 ∙х. Форма записи уравнения имеет вид уравнения Лагранжа: y=φ(y′)∙x+ψ(y′), где φ(y′)=
∙х. Форма записи уравнения имеет вид уравнения Лагранжа: y=φ(y′)∙x+ψ(y′), где φ(y′)= 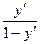 и ψ(y′)=0.
и ψ(y′)=0.
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p → исходное уравнение принимает вид: y=φ(p)∙x+ψ(p)=x∙ 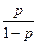 .
.
a2. Дифференцируя последнее по x имеем: p–φ(p)=[x∙φ′(p)+ψ′(p)] 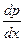 .
.
a3. Запишем равенство: p–φ(p)= – 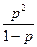 =0, его решения: p0=0. Учитывая p0 ≡φ(p0), запишем: y=φ(p0)∙x+ψ(p0) → y= 0∙x+0= 0. Пока не получено общее решение уравнения, мы не можем сказать, будет ли это решение особыми.
=0, его решения: p0=0. Учитывая p0 ≡φ(p0), запишем: y=φ(p0)∙x+ψ(p0) → y= 0∙x+0= 0. Пока не получено общее решение уравнения, мы не можем сказать, будет ли это решение особыми.
a4. Пусть теперь p–φ(p) ≠ 0. Уравнение для вычисления x: 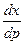 –x
–x 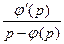 =
= 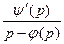 , или
, или 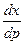 + x
+ x 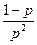 ∙
∙ 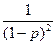 =0, или
=0, или 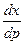 = x
= x 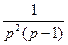 уравнение с разделяющимися переменными.
уравнение с разделяющимися переменными.
a5. Интегрируем уравнение (предварительно разложив дробь 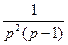 : осуществляется по общей формуле разложения, используемой при интегрировании рациональных дробей: см. математический анализ!):
: осуществляется по общей формуле разложения, используемой при интегрировании рациональных дробей: см. математический анализ!): 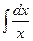 = –
= – 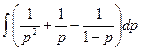 =
= 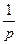 –ln
–ln 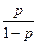 +C, или в виде: Получаем после несложных преобразований:
+C, или в виде: Получаем после несложных преобразований:
ln 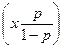 =
= 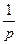 +C.
+C.
a6. Если учесть исходное: y=x∙ 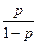 , то
, то 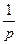 =
= 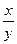 –1. Тогда lny=
–1. Тогда lny= 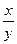 +1+C, или
+1+C, или 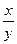 =C+lny – общее решение исходного уравнения.
=C+lny – общее решение исходного уравнения.
a7. Учитывая начальные условия, получим: 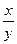 =3+lny – частное решение, для C=3.
=3+lny – частное решение, для C=3.
Замечание: рассмотренная задача была решена в Главе 2 приведением к форме однородного уравнения; результаты получены одинаковые, но на этот раз потребовались дополнительные «изобретательность и терпенье» для достижения «одинаковости».
Ответ: 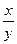 =3±lny – частный интеграл заданного уравнения. Особое решение: y = 0.
=3±lny – частный интеграл заданного уравнения. Особое решение: y = 0.
☻
Вопросы для самопроверки:
1. Как определяют ДУ 1-го порядка, не разрешённое относительно производной?
2. Основные типы уравнений, не разрешённых относительно производной.
3. Как вводят параметр при решении уравнения y=φ(y′)?
4. Как вводят параметр при решении уравнения x=φ(y′)?
5. Как вводят параметр при решении уравнения F(y,y′)=0?
6. Как вводят параметр при решении уравнения F(x,y′)=0?
7. Что такое «Уравнения Лагранжа»?
8. Привести пример применения ДУ для решения задачи из геометрии.
9. Привести пример применения ДУ для решения задачи из физики.
< * * * * * >
