Уравнения, не разрешенные относительно производной

5.1 Метод «интегрирования посредством дифференцирования»

В общем случае уравнение, не разрешенное относительно производной

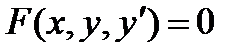(1)

представим в эквивалентном виде

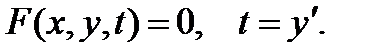(2)

Ищем решение в параметрической форме 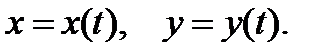Учитывая первое соотношение (2), найдем дифференциал функции F:

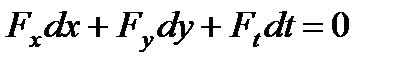. (3)

Используя связь dy = t dx, исключим последовательно dy и dx в выражении (3). В результате приходим к системе двух дифференциальных уравнений

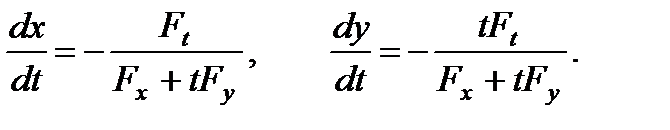(4)

Если удается решить эту систему, то решение исходного уравнения (1) получается

в параметрической форме x = x(t), y = y(t).

Замечание 1 . При использовании данного метода возможна потеря отдельных решений (этот вопрос надо исследовать дополнительно).

Замечание 2. Этот метод особенно удобен, если уравнение (1) легко разрешается относительно у (или х). Тогда, дифференцируя полученное выражение по х (или по у) и, считая t функцией от х (или от у), получим уравнение, разрешенное относительно производной.

П р и м е р 10. Проинтегрировать уравнение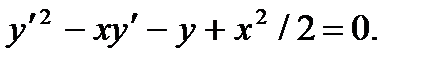

Полагая 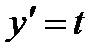, находим 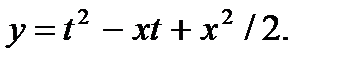Дифференцируем по х, считая t функцией от х и заменяя 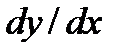через t, имеем

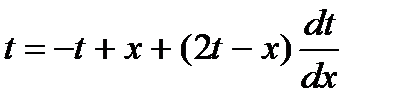или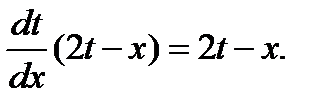

Отсюда следуют два уравнения:

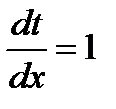и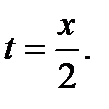

Из первого уравнения t = x + C. Подставляя это в подчеркнутое выражение для у, находим общее решение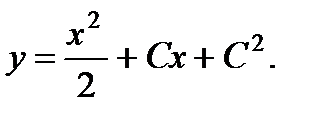

Подставляя 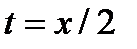туда же, получим особое решение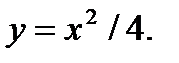

Если из исходного уравнения выразить х, то полученное выражение следует

дифференцировать по у, считая t функцией от у и заменяя 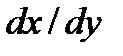на .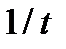

5.2 Уравнения вида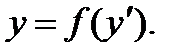

Это уравнение является частным случаем уравнения (1) при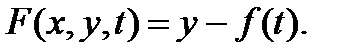

Процедура, описанная в разд. 5.1, приводит к уравнениям

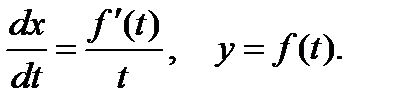(5)

Здесь вместо второго уравнения системы (4) использовано исходное уравнение (так можно делать поскольку первое уравнение системы не зависит от у).

Интегрируя первое уравнение (5), получим решение в параметрическом виде

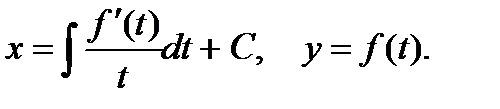
5.3 Уравнения вида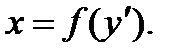

Это уравнение является частным случаем уравнения (1) при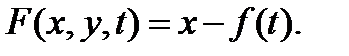

Процедура, описанная в разд. 5.1, приводит к уравнениям

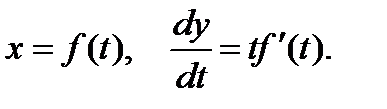(6)

Здесь вместо первого уравнения системы (4) использовано исходное уравнение (так можно делать поскольку второе уравнение системы не зависит от х).

Интегрируя второе уравнение (6), получим решение в параметрическом виде

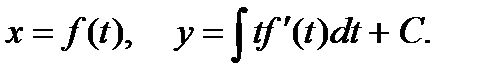
5.4 Уравнение Клеро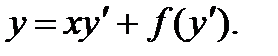

Уравнение Клеро является частным случаем уравнения (1) при

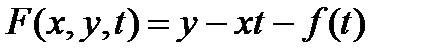и может быть записано в виде

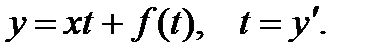(7)

Заменяя в равенстве 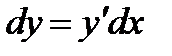величины 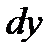и 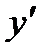их значениями из (7), приходим к уравнению

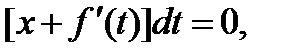
Которое распадается на два уравнения: dt = 0 и 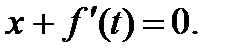Решение первого очевидно: t = C.Оно дает общее решение уравнения Клеро

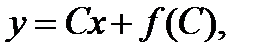(8)

Представляющее собой семейство прямых. Второе уравнение дает решение в параметрической форме

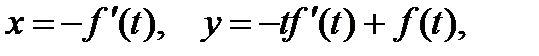
Которое является особым и представляет собой огибающую семейства прямых (8).

5.5 Уравнение Лагранжа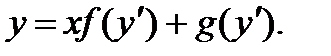

Уравнение Лагранжа является частным случаем уравнения (1) при

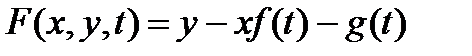. В частном случае 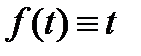оно совпадает с уравнением Клеро (см. разд. 5.4). Процедура, описанная в разд. 5.1, приводит к уравнениям

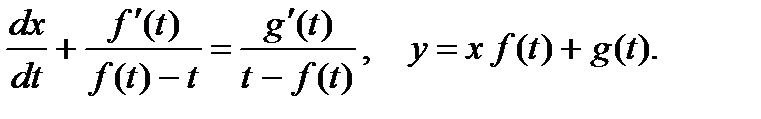(9)

Здесь вместо второго уравнения системы (4) использовано исходное уравнение (так можно делать поскольку первое уравнение системы не зависит от у).

Первое уравнение системы (9) является линейным. Его общее решение имеет вид

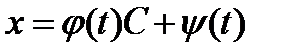(функция 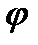и 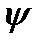определяются по формулам из разд. 2.5). Подставляя это выражение во второе равенство (9), находим общее решение уравнения Лагранжа в параметрической форме

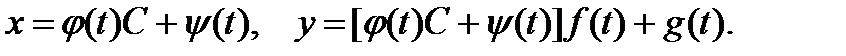
Замечание 3. Данный метод может привести к потере решений вида 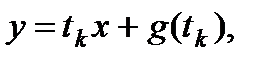где t_k – корни уравнения f(t) – t = 0. Эти решения могут быть как частными, так и особыми.