Необходимый признак сходимости ряда

При исследовании рядов одним из основных вопросов является вопрос о том, сходится или расходится ряд. Установим условие, при невыполнении которого ряд расходится. Такое условие называется необходимым условием сходимости ряда.

Теорема. Если ряд (1) сходится, то его п-ый член стремится к нулю при неограниченном возрастании п.

Д о к а з а т е л ь с т в о. Если ряд сходится, то 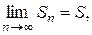также справедливо и равенство 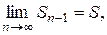но u_n = S_n – S_n-1, или, поскольку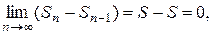

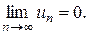(4)

Теорема доказана.

Следствие. Если п-ый член ряда не стремится к нулю при п ® ¥, то ряд расходится.

Замечание. Подчеркнём, что из условия, что п-ый член стремится к нулю, ещё не следует, что ряд сходится.

Элементарные свойства рядов

Свойство 1.Сходимость ряда не нарушится, если все его члены умножить на одно и то же число.

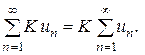
Свойство 2.Сумма (разность) двух сходящихся рядов - ряд сходящийся.

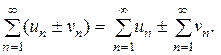
Свойство 3. Ряд 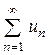сходится, если соответствующий ряд, составленный из модулей 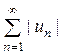- сходящийся. Такой ряд называется абсолютно сходящимся.

Если ряд (1) сходится, а ряд 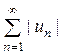расходится, то ряд называется условно сходящимся.

Свойство 3 является следствием свойства 2.

Свойство 4. Если в ряде (1) отбросить конечное число начальных членов, например, р членов, то получим ряд:

u_p+1+ u_p+2+ u_p+3+…+ u_n+…,

который сходится или расходится одновременно с данным. Это означает, что при исследовании ряда на сходимость можно игнорировать конечное число его членов.

Свойство 5. Если члены ряда (1) неотрицательны, а его частичные суммы ограничены, то такой ряд сходится.

Признак сравнения рядов

Если члены ряда (1) неотрицательны и не превосходят соответствующих членов сходящегося ряда

v₁+ v₂+ v₃+…+ v_n+…,

то ряд (1) также сходится.

Д о к а з а т е л ь с т в о. Запишем частичные суммы рядов

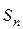= u₁+ u₂+ u₃+…+ u_n,

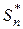= v₁+ v₂+ v₃+…+ v_n,

где u₁ £ v₁, u₂ £ v₂, ¼ По условию 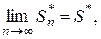тогда S_n £ S^* и по свойству 5 ряд (1) сходится.

Замечание. Согласно свойству 4, признак сравнения рядов остается в силе, если соответствующие неравенства между их членами выполнены, начиная с некоторого номера n ³ N.

Пример 5. Установить сходимость ряда

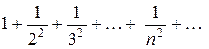
Отбросим первый член этого ряда и сравним его со сходящимся рядом (см. пример 4)

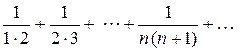
Так как

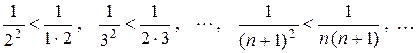
то на основании признака сравнения рядов исходный ряд сходится.

Достаточные признаки сходимости

Представленные далее достаточные признаки сходимости являются одними из многих признаков.

Признак Даламбера

Пусть все члены ряда (1) положительны и пусть при n®¥

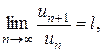(5)

тогда, а) если l < 1, то ряд сходится; б) если l > 1, то ряд расходится; в) если l = 1, признак ответа не дает.

Д о к а з а т е л ь с т в о. а) l < 1. Выберем число q, такое, что l < < q < 1. Из определения предела 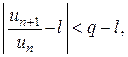начиная с n ³ N,тогда 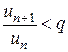при n ³ N. Откуда для n=N, N+1, N+2, N+3, ¼ будем иметь: u_N+1 < q u_N,

u_N+2 < q u_N+1 < q² u_N ,

u_N+3 < q u_N+2 < q³ u_N ,

……………………...,

т.е., если в ряде (1) отбросить первые N-1 членов, то получится ряд

u_N+ u_N+1+ u_N+2+¼,

члены которого меньше соответствующих членов сходящегося геометрического ряда со знаменателем q < 1:

u_N + q u_N + q² u_N +…

На основании признака сравнения и свойства 4, ряд (1) также сходится. Случай б) доказывается аналогично. В случае в) ряд может быть как сходящимся, так и расходящимся.

Признак Коши