Понятие дифференциала функции

Санкт-Петербургский университет Государственной противопожарной службы

МЧС России

––––––––––––––––––––––––––––––––––––––––––––––––––––––

Кафедра прикладной математики и информационных технологий

УТВЕРЖДАЮ

Начальник кафедры прикладной математики

и информационных технологий

полковник внутренней службы

С.Л. Исаков

25 апреля 2008 года

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

ДЛЯ ПРОВЕДЕНИЯ ПРАКТИЧЕСКОГО ЗАНЯТИЯ

по учебной дисциплине «Математика»

Тема № 5 «Элементы функционального анализа»

Занятие № 5.1 «Дифференциал функции»

Рассмотрена на заседании кафедры прикладной математики и информационных технологий

Протокол № 10_

от 25 апреля 2008 года

Санкт-Петербург

I. Общеобразовательные цели

1. Изучить понятие дифференциала функции

2. Получить основные теоремы дифференциального исчисления

II. Дидактические цели

1. Изучить понятие дифференциала, правило Лапиталя

III Воспитательные цели

1. Воспитывать у обучаемых стремление к углубленному освоению учебного материала, связанного с их практической деятельностью.

2. Развивать навыки логического и абстрактного мышления у обучаемых.

III. Расчет учебного времени

Содержание и порядок проведения занятия	Время, мин
ВСТУПИТЕЛЬНАЯ ЧАСТЬ   ОСНОВНАЯ ЧАСТЬ Учебные вопросы: 1. Понятие дифференциала функции 2. Основные теоремы дифференциального исчисления 3. Правило Лапиталя     ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ

IV. Учебно-материальное обеспечение

1. Высшая математика для экономистов. В.Г. Григулецкий, З.В.Ященко. «Феникс», - 2004, - 632 с.

2. Высшая математика для экономистов. Н.Ш. Крамер. «ЮНИТИ», - 2004, - 470с.

3. Мультимедийный проектор

V. Методические рекомендации преподавателю

По подготовке к проведению практического занятия

При подготовке к занятию преподаватель обязан ознакомиться с литературой и методическими рекомендациями, изучить учебные вопросы, структуру и содержание практического занятия. По завершении личной теоретической подготовки необходимо составить план проведения лекции с указанием времени, отводимого на отработку учебного вопроса. Разработать и выдать обучаемым задания на подготовку к практическому занятию, дать указания на получение необходимой литературы, учебно-методических материалов и рекомендовать материал для повторения.

Во вступительной части занятия (5 мин) после проверки наличия личного состава, объявить тему, цели и учебные вопросы занятия, последовательность их отработки, ориентировочное время отводимое на учебные вопросы..

При отработке первого учебного вопроса (30 мин) рассматривается понятие дифференциала функции,

При отработке второго учебного вопроса (20 мин) рассматривается основные теоремы дифференциального исчисления.

При отработке третьего учебного вопроса (20 мин) рассматривается правило Лапиталя.

В заключительной части (5 мин)подвести итоги занятия, поставить задачи на следующее занятие.

VI. Литература, рекомендованная преподавателю

Основная:

1. Высшая математика для экономистов. В.Г. Григулецкий, З.В.Ященко. «Феникс», - 2004, - 632 с.

2. Высшая математика для экономистов. Н.Ш. Крамер. «ЮНИТИ», - 2002, - 470с.

Дополнительная:

1. Щипачев В.С.. Высшая математика: Учебник для вузов. – 5 изд., стер. - М.: Высшая школа, 2001. – 254 с.

2. Высшая математика: Методические указания и контрольные задания для слушателей заочного обучения /Составители: Алексеик Е.Б., Финоженок Г.Н., Исаков С.Л., Урюпин А.Н.//Под ред. В.С. Артамонова. – СПб.: СПб институт ГПС МЧС России, 2003. -112 с.

VII. Приложение

1. Задание к проведению практического занятия.

Разработал

Начальник кафедры прикладной математики и информационных технологий

полковник внутренней службы С.Л. Исаков

ЗАДАНИЕ К ПРОВЕДЕНИЮ ПРАКТИЧЕСКОГО ЗАНЯТИЯ

по дисциплине «Математика»

I. Учебные вопросы

Понятие дифференциала функции

С понятием производной тесно связано понятие Дифференциала

пусть некоторая функция 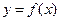+ имеет в точке производную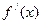

Придадим аргументу приращение ∆x, тогда ∆y – соответствующее ему приращение функции.

ПО определению производной 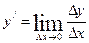, следовательно 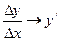при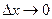

на основании теоремы из теории пределов, 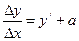, где a- бесконечно малая величина.

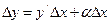. приращение функции = сумме двух слагаемых.

первое слагаемое называется дифференциалом функции и обозначается dy.

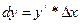т.к. ∆x=dx →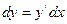

Геометрический дифференциал функции представляет собой приращение ординат точки, лежащей на касательной к графику функции

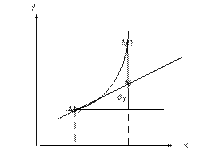
С уменьшением ∆x уменьшается разница между dy и ∆y.

По этому в приближенных вычислениях при малых ∆x можно приращение функции заменять дифференциалом функции.

Алгоритм приближенных вычислений при помощи дифференциала.

1.

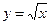
2.

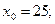
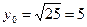
3.

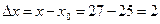
4.

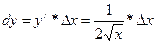
5.

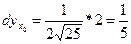
находим значение дифференциала в точке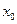

6. новое значение функции = значению функции 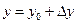. т. к. приращение функции сложно найти она заменяется дифференциалом:

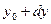
Проверим: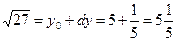

Пример: найти дифференциал функции

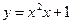в точке x=2

двумя способами:

1. выделяя линейную относительно ∆x часть приращения функции ∆y.

2. по формуле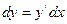

Решение:

1.

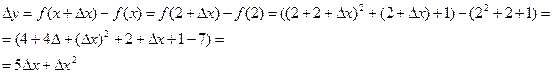
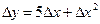
Выделяя линейную относительно 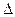x часть приращения функции получаем что .

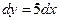2. находим дифференциал по формуле 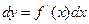.
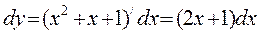