Подведение функции под знак дифференциала

Интегрирование по частям. Примеры решений

И снова, здравствуйте. Сегодня на уроке мы научимся интегрировать по частям. Метод интегрирования по частям – это один из краеугольных камней интегрального исчисления. На зачете, экзамене студенту почти всегда предлагают решить интегралы следующих типов: простейший интеграл (см. статьюНеопределенный интеграл. Примеры решений) либо интеграл на замену переменной (см. статьюМетод замены переменной в неопределенном интеграле)либо интеграл как раз на метод интегрирования по частям.

Для эффективного изучения темы необходимо хорошо ориентироваться в материалах двух вышеуказанных уроков. Если Вы чайник, и только-только начинаете погружение в удивительный мир интегралов, то читать далее не имеет особого смысла – следует начать с урока Неопределенный интеграл. Примеры решений.

Как всегда, под рукой должны быть: Таблица интегралов и Таблица производных. Если у Вас до сих пор их нет, то, пожалуйста, посетите кладовку моего сайта: Математические формулы и таблицы. Не устану повторять – лучше всё распечатать. Весь материал я постараюсь изложить последовательно, просто и доступно, в интегрировании по частям нет особых трудностей.

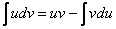Какую задачу решает метод интегрирования по частям? Метод интегрирования по частям решает очень важную задачу, он позволяет интегрировать некоторые функции, отсутствующие в таблице, произведение функций, а в ряде случаев – и частное. Как мы помним, нет удобной формулы: . Зато есть такая: – формула интегрирования по частям собственной персоной. Знаю, знаю, ты одна такая – с ней мы и будем работать весь урок (уже легче).

И сразу список в студию. По частям берутся интегралы следующих видов:

1) 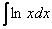, , 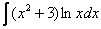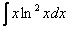– логарифм, логарифм, умноженный на какой-нибудь многочлен.

2) 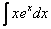, 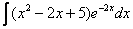– экспоненциальная функция, умноженная на какой-нибудь многочлен. Сюда же можно отнести интегралы вроде 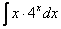– показательная функция, умноженная на многочлен, но на практике процентах так в 97, под интегралом красуется симпатичная буква «е». … что-то лирической получается статья, ах да… весна же пришла.

3) 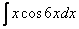, , 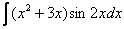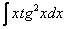– тригонометрические функции, умноженные на какой-нибудь многочлен.

4) 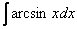, 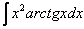– обратные тригонометрические функции («арки»), «арки», умноженные на какой-нибудь многочлен.

Также по частям берутся некоторые дроби, соответствующие примеры мы тоже подробно рассмотрим.

Интегралы от логарифмов

Пример 1

Найти неопределенный интеграл.

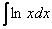
Классика. Время от времени данный интеграл можно встретить в таблицах, но пользоваться готовым ответом нежелательно, так как у преподавателя весенний авитаминоз и он сильно заругается. Потому что рассматриваемый интеграл отнюдь не табличный – он берётся по частям. Решаем:

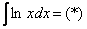
Прерываем решение на промежуточные объяснения.

Используем формулу интегрирования по частям: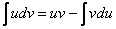

Определенный интеграл. Примеры решений

И снова здравствуйте. На данном уроке мы подробно разберем такую замечательную вещь, как определенный интеграл. На этот раз вступление будет кратким. Всё. Потому что снежная метель за окном.

Для того чтобы научиться решать определенные интегралы необходимо:

1) Уметь находить неопределенные интегралы.

2) Уметь вычислить определенный интеграл.

Как видите, для того чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще совсем не закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений.

В общем виде определенный интеграл записывается так:

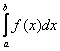
Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования.

Нижний предел интегрирования стандартно обозначается буквой .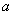
Верхний предел интегрирования стандартно обозначается буквой .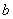
Отрезок 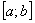называется отрезком интегрирования.

Прежде чем мы перейдем к практическим примерам, небольшое «факью» по определенному интегралу.

Что такое определенный интеграл? Считаю немного преждевременным рассказать про разбиения отрезка и предел интегральных сумм, поэтому пока я скажу, что определенный интеграл – это ЧИСЛО. Да-да, самое что ни на есть обычное число.

Есть ли у определенного интеграла геометрический смысл? Есть. И очень хороший. Самая популярная задача – вычисление площади с помощью определенного интеграла.

Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.

Как решить определенный интеграл?С помощью знакомой со школы формулы Ньютона-Лейбница:

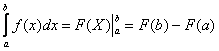
Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.

Этапы решения определенного интеграла следующие:

1) Сначала находим первообразную функцию 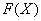(неопределенный интеграл). Обратите внимание, что константа 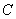в определенном интеграле не добавляется. Обозначение 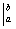является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись 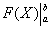? Подготовка для применения формулы Ньютона-Лейбница.

2) Подставляем значение верхнего предела в первообразную функцию: .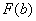

3) Подставляем значение нижнего предела в первообразную функцию: .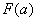

4) Рассчитываем (без ошибок!) разность 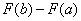, то есть, находим число.

Готово.

Всегда ли существует определенный интеграл? Нет, не всегда.

Например, интеграла 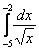не существует, поскольку отрезок интегрирования 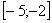не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример: 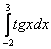. Такого интеграла тоже не существует, так как в точках 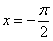, 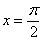отрезка 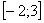не существует тангенса. Кстати, кто еще не прочитал методический материал Графики и основные свойства элементарных функций – самое время сделать это сейчас. Будет здорово помогать на протяжении всего курса высшей математики.

Для того чтобы определенный интеграл вообще существовал, достаточно чтобы подынтегральная функция быланепрерывнойна отрезке интегрирования.

Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывнана отрезке интегрирования. По студенческой молодости у меня неоднократно бывал казус, когда я подолгу мучался с нахождением трудной первообразной, а когда наконец-то ее находил, то ломал голову еще над одним вопросом: «что за ерунда получилась?». В упрощенном варианте ситуация выглядит примерно так:

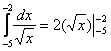???! Нельзя подставлять отрицательные числа под корень! Что за фигня?! Изначальная невнимательность.

Если для решения (в контрольной работе, на зачете, экзамене) Вам предложен несуществующий интеграл вроде 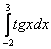, то нужно дать ответ, что интеграла не существует и обосновать – почему.

Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл, коим отведена отдельная лекция.

Может ли нижний предел интегрирования быть больше верхнего предела интегрирования?Может, и такая ситуация реально встречается на практике.

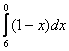– интеграл преспокойно вычисляется по формуле Ньютона-Лейбница.

Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.

В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:

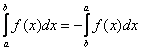
Например, в определенном интеграле перед интегрированием 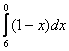целесообразно поменять пределы интегрирования на «привычный» порядок:

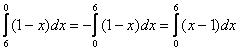– в таком виде интегрировать значительно удобнее.

Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:

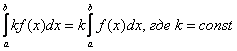
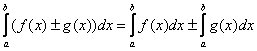– это справедливо не только для двух, но и для любого количества функций.

В определенном интеграле можно проводить замену переменной интегрирования, правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.

Для определенного интеграла справедлива формула интегрирования по частям:

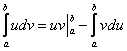
Пример 1

Вычислить определенный интеграл

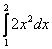
Решение:

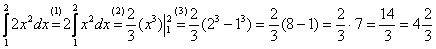
(1) Выносим константу за знак интеграла.

(2) Интегрируем по таблице с помощью самой популярной формулы 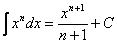. Появившуюся константу 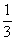целесообразно отделить от 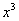и вынести за скобку. Делать это не обязательно, но желательно – зачем лишние вычисления?

(3) Используем формулу Ньютона-Лейбница 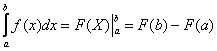. Сначала подставляем в 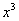верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.

Пример 2

Вычислить определенный интеграл

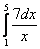
Это пример для самостоятельно решения, решение и ответ в конце урока.

Немного усложняем задачу:

Пример 3

Вычислить определенный интеграл

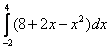
Решение:

(1) Используем свойства линейности определенного интеграла.

(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.

(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:

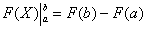
СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряю на третьем слагаемом: 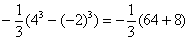– первое место в хит-параде ошибок по невнимательности, очень часто машинально пишут 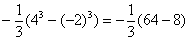(особенно, когда подстановка верхнего и нижнего предела проводится устно и не расписывается так подробно). Еще раз внимательно изучите вышерассмотренный пример.

Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, я сам привык решать подобные интегралы так:

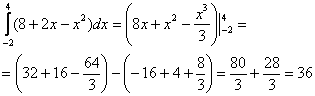
Здесь я устно использовал правила линейности, устно проинтегрировал по таблице. У меня получилась всего одна скобка с отчёркиванием пределов: 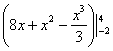(в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию, я сначала подставил сначала 4, затем –2, опять же выполнив все действия в уме.

Какие недостатки у короткого способа решения? Здесь всё не очень хорошо с точки зрения рациональности вычислений, но лично мне всё равно – обыкновенные дроби я считаю на калькуляторе.
Кроме того, существует повышенный риск допустить ошибку в вычислениях, таким образом, студенту-чайнику лучше использовать первый способ, при «моём» способе решения точно где-нибудь потеряется знак.

Однако несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная 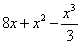находится в одной скобке.

Подведение функции под знак дифференциала

На уроке Неопределенный интеграл. Примеры решениймы научились раскрывать дифференциал, напоминаю пример, который я приводил:

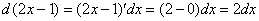
То есть, раскрыть дифференциал – это формально почти то же самое, что найти производную.

Пример 1

Найти неопределенный интеграл. Выполнить проверку.

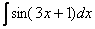
Смотрим на таблицу интегралов и находим похожую формулу: 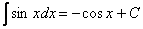. Но проблема заключается в том, что у нас под синусом не просто буковка «икс», а сложное выражение. Что делать?

Подводим функцию 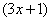под знак дифференциала:

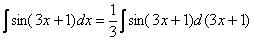
Раскрывая дифференциал, легко проверить, что:

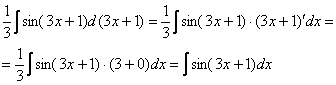
Фактическ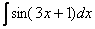и и 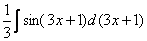– это запись одного и того же.

Но, тем не менее, остался вопрос, а как мы пришли к мысли, что на первом шаге нужно записать наш интеграл именно так: 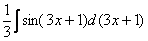? Почему так, а не иначе?

Формула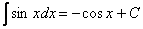 (и все другие табличные формулы) справедливы и применимы НЕ ТОЛЬКО для переменной 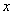, но и для любого сложного выражения ЛИШЬ БЫ АРГУМЕНТ ФУНКЦИИ( 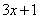– в нашем примере) И ВЫРАЖЕНИЕ ПОД ЗНАКОМ ДИФФЕРЕНЦИАЛА БЫЛИОДИНАКОВЫМИ.

Поэтому мысленное рассуждение при решении должно складываться примерно так: «Мне надо решить интеграл 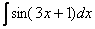. Я посмотрел в таблицу и нашел похожую формулу 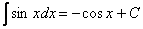. Но у меня сложный аргумент 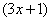и формулой я сразу воспользоваться не могу. Однако если мне удастся получить 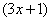и под знаком дифференциала, то всё будет нормально. Если я запишу 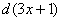, тогда 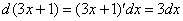. Но в исходном интеграле 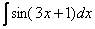множителя-тройки нет, поэтому, чтобы подынтегральная функция не изменилась, мне надо ее домножить на 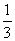». В ходе примерно таких мысленных рассуждений и рождается запись:

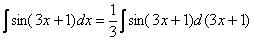
Теперь можно пользоваться табличной формулой :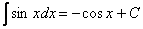

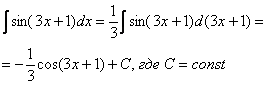
Готово

Единственное отличие, у нас не буква «икс», а сложное выражение .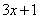

Выполним проверку. Открываем таблицу производных и дифференцируем ответ:

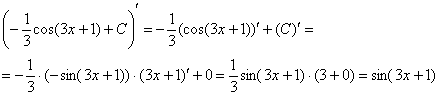
Получена исходная подынтегральная функция, значит, интеграл найден правильно.

Обратите внимание, что в ходе проверки мы использовали правило дифференцирования сложной функции 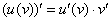. По сути дела подведение функции под знак дифференциала и 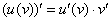– это два взаимно обратных правила.

Пример 2

Найти неопределенный интеграл. Выполнить проверку.

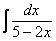
Анализируем подынтегральную функцию. Здесь у нас дробь, причем в знаменателе линейная функция (с «иксом» в первой степени). Смотрим в таблицу интегралов и находим наиболее похожую вещь: .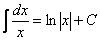

Подводим функцию 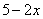под знак дифференциала:

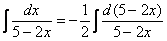
Те, кому трудно сразу сообразить, на какую дробь нужно домножать, могут быстренько на черновике раскрыть дифференциал: 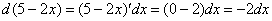. Ага, получается 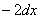, значит, чтобы ничего не изменилось, мне надо домножить интеграл на .
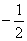Далее используем табличную формулу :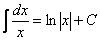

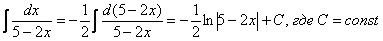
Проверка:

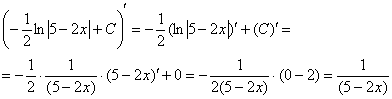
Получена исходная подынтегральная функция, значит, интеграл найден правильно.

Пример 3

Найти неопределенный интеграл. Выполнить проверку.

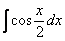
Это пример для самостоятельного решения. Ответ в конце урока.

Пример 4

Найти неопределенный интеграл. Выполнить проверку.

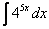
Это пример для самостоятельного решения. Ответ в конце урока.

При определенном опыте решения интегралов, подобные примеры будут казаться лёгкими, и щелкаться как орехи:

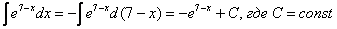
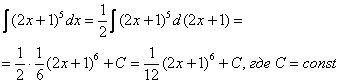
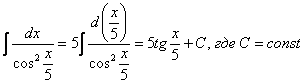
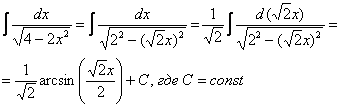
И так далее.

В конце данного параграфа хотелось бы еще остановиться на «халявном» случае, когда в линейной функции переменная 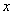входит с единичным коэффициентом, например:

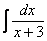
Строго говоря, решение должно выглядеть так:

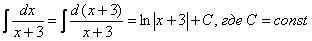
Как видите, подведение функции 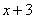под знак дифференциала прошло «безболезненно», без всяких домножений. Поэтому на практике таким длинным решением часто пренебрегают и сразу записывают, что 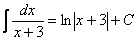. Но будьте готовы при необходимости объяснить преподавателю, как Вы решали! Поскольку интеграла 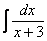в таблице вообще-то нет.