Квадратные уравнения (26 ч).

Квадратное уравнение. Неполное квадратное уравнение. Формулы корней квадратного уравне­ния. Теорема Виета. Решение уравнений, сводящихся к квадратным уравнениям, дробно-рациональных. Решение задач, приводящих к квадратным и рациональным уравнениям.

Основная цель — выработать умения решать квадрат­ные уравнения (полные и неполные), дробно-рациональные, а также уравнения, сводящиеся к квадратным и при­менять их к решению задач.

Основное внимание уделяется решению уравнений вида ах² + вх + с = 0, где а 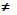0, по формуле корней. Для вывода формулы рассматривается пример решения квад­ратного уравнения с помощью выделения квадрата двучлена из квадратного трехчлена, на котором разъясняется прием, ис­пользуемый затем при выводе формулы в общем виде.

Особое внимание уделяется теореме Виета, выражающей зависимость между корнями квадратного урав­нения и его коэффициентами и составлению уравнения с заданными корнями.

При рассмотрении дробных рациональных уравнений обращается внимание учащихся на необходимость дополни­тельных исследований, позволяющих исключить посторонние корни. На материале данной темы учащиеся получают представление о графическом методе решения уравнений.

Изучение данной темы позволяет существенно расширить аппарат уравнений, используемый для решения текстовых за­дач.

Уровень обязательной подготовки обучающегося

Уметь решать квадратные уравнения и дробные рациональные уравнения.

 Уметь решать несложные текстовые задачи с помощью уравнений.

Уровень возможной подготовки обучающегося

· Понимать, что уравнения – это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики.

· Уметь решать квадратные уравнения, дробные рациональные уравнения.

· Уметь применять квадратные уравнения и дробные рациональные уравнения при решении задач.

Уровень обязательной подготовки выпускника

Уровень возможной подготовки выпускника

Неравенства (19 ч).

Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Применение свойств не­равенств к оценке значения выражения. Линейное неравенст­во с одной переменной. Система линейных неравенств с од­ной переменной. Линейные неравенства с модулем.

Основная цель — выработать умение решать линей­ные неравенства с одной переменной и их системы.

Свойства числовых неравенств составляют ту базу, на кото­рой основано решение линейных неравенств с одной перемен­ной. При доказательстве этих свойств учащиеся знакомятся с приемом доказательства неравенств, состоящим в сравнении с нулем разности левой и правой частей неравенств. Примене­ние свойств неравенств для оценки значений выражений показывается при выполнении простейших упражнений.

При решении неравенств используются свойст­ва равносильности неравенств, которые разъясняются на кон­кретных примерах. Особое внимание уделяется отработ­ке умения решать простейшие неравенства вида ах>в, ах<в, остановившись специально на случае, когда а < 0.

Умение решать линейные неравенства является опорным для решения систем двух линейных неравенств с одной пере­менной, в частности таких, которые записаны в виде двойного неравенства, а также неравенств с модулем.