Третий этап метода конечных разностей

КУРСОВАЯ РАБОТА

«Решение краевой задачи линейно-дифференциального уравнения 2-го порядка»

Работу выполнил

студент группы 1-СУЗС-1

Трапезников Н.А.

Работу приняла доцент

Букунова О.В

Санкт-Петербург

Понятие краевой задачи

Решение дифференциального уравнения – функция, которая, будучи подставлена в уравнение, обращает его в тождество.

Выделяются общие и частные решения дифференциального уравнения. Общее решение дифференциального уравнения имеет вид:

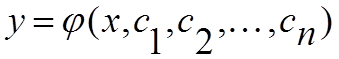
где с - произвольные постоянные.

Частное решение – такое решение, которое получается из общего при определенном значении произвольной постоянной c.

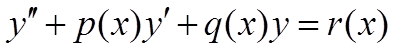Для нахождения частного решения уравнения второго порядка вида:

где p(x), q(x), r(x) - заданные функции.

требуется задать два условия. В зависимости от вида этих условий различают две задачи: задачу Коши, краевую задачу.

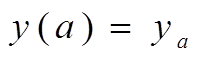
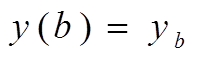В случае краевой задачи задаются значения искомой функции в каких-либо двух точках интервала интегрирования:

Решение краевой задачи методом конечных разностей (метод сеток)

Алгоритм метода заключается в выполнении следующих трех этапов:

1. Замена области непрерывного изменения аргумента областью его дискретного изменения;

2. Замена дифференциального оператора некоторым разностным оператором, формулировка разностного аналога для граничных условий;

3. Решение полученной в результате осуществления первых трех этапов алгебраической системы линейный уравнений

Первый этап метода конечных разностей

Требуется найти решение дифференциального уравнения на определенном отрезке. Выбираем произвольное число разбиений отрезка – n. Тогда получим (n+1) узел разностной сетки:

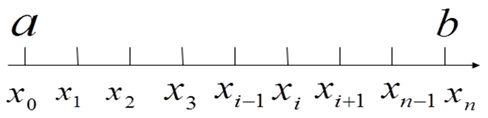
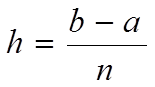Шаг сетки h определяется по формуле:

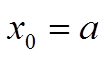
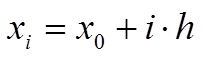
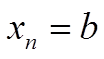Сами узлы вычисляются так:

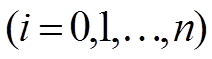Узлы сетки x₀, x_n - граничные узлы, x₁,x₁,x₃...x_n-1 - внутренние узлы разностной сетки.

Второй этап метода конечных разностей

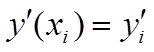
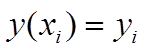
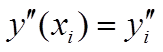Второй этап - замена производных, входящих в данное дифференциальное уравнение, соответствующими конечно-разностными соотношениями. Для этого необходимо выразить значение первой производной в произвольном узле . Введем обозначения:

Рассмотрим три последовательных узла сетки x_i-1, x_i, x_i+1 (рис.1).

Второй этап метода конечных разностей (Рис.1)

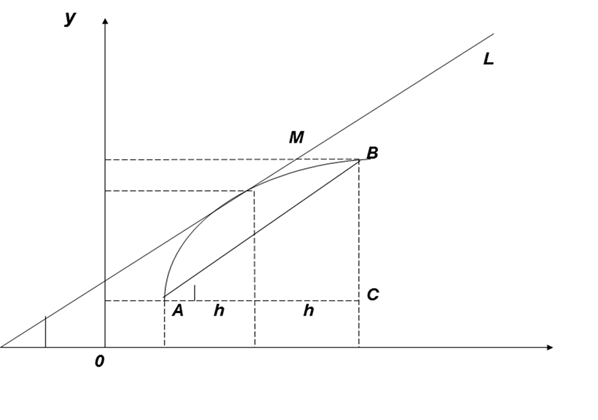
В треугольнике АВС стороны АС=2h,

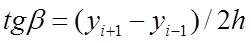ВС=y_i+1-y_i-1, тогда

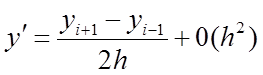
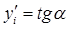
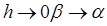
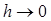Проведем касательную ML к кривой y(x) в точке M(x_i,y_i). Обозначим через угол наклона касательной с осью абсцисс. Как известно, касательная – это предельное положение секущей АВ, когда , поэтому при Согласно геометрическому смыслу производной, имеем . Сравнивая выражения , получим аппроксимацию первой производной:

где 0(h²) - бесконечно малая порядка h² . (1)

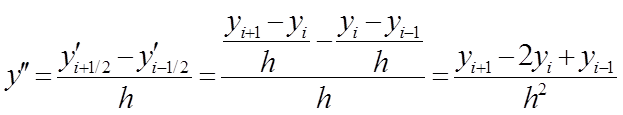
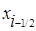
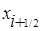
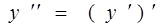Для вывода формулы второй производной в разностном виде воспользуемся тем, что , а первую производную запишем по формуле (1) в промежуточных узлах и :

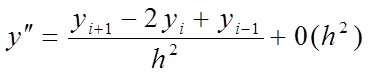Окончательное выражение второй производной:

(2)

Третий этап метода конечных разностей

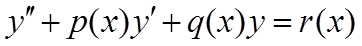Рассмотрим линейное дифференциальное уравнение второго порядка:

где p(x), q(x), r(x) - заданные функции.

Обозначим: p(x)=p_i , q(x)=q_i , r(x)=r_i .

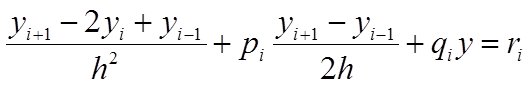Используя формулы (1) и (2), перепишем уравнение следующим образом:

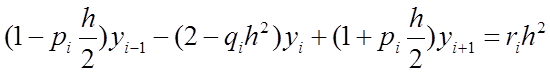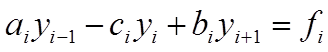Запишем полученное уравнение в следующей форме:

, где:

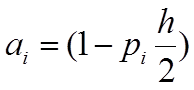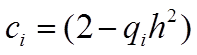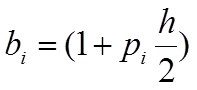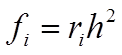Записав уравнение для всех внутренних узлов сетки, получим систему линейных алгебраических уравнений, состоящую из (n-1) уравнений и содержащую (n+1) неизвестных (y₀,y₁,...y_n) . Недостающие два уравнения получаются из краевых условий.
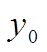
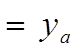
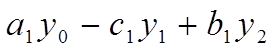
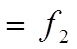
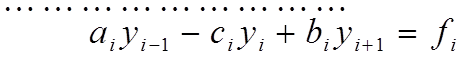
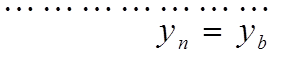