Теоретические сведения и примеры. Пусть функция f (х)определена и непрерывна на отрезке и имеет на данном отрезке

Пусть функция f (х)определена и непрерывна на отрезке 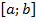и имеет на данном отрезке конечное число критических точек (точек, в которых производная обращается в нуль или не существует). Тогда функция на отрезке 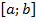достигает своего наибольшего (соответственно, наименьшего) значения либо на одном из концов этого отрезка, либо в критической внутренней точке этого отрезка. Чтобы найти наибольшее и наименьшее значения функции на отрезке 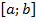, следует первоначально убедиться, что функция на отрезке непрерывна, а затем:

1) найти значения функции на концах отрезка, т. е. вычислить ;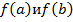

2) с помощью производной 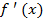найти критические точки, принадлежащие интервалу 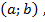и вычислить в них значение функции;

3) из всех полученных значений функции выбрать наибольшее и наименьшее.

Пример 1. Найти наибольшее и наименьшее значения функции 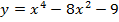на отрезке .

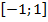Решение. Найдем значение функции на концах отрезка:

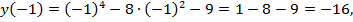
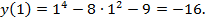
Функция определена и непрерывна на отрезке 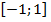. Найдем критические точки:

;

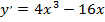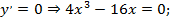
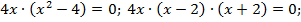
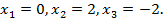
Отрезку принадлежит только значение х = 0. Вычислим значение функции в этой точке: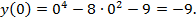

Ответ: выбор из полученных значений 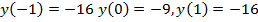показывает, что наибольшим значением функции на отрезке является, 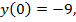а наименьшим _.

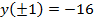Пример 2. Найти наибольшее и наименьшее значение функции 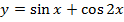на отрезке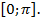

Решение. Вычислим значения функции на концах отрезка: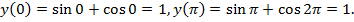

Определим критические точки:

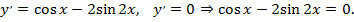
Решим полученное тригонометрическое уравнение:

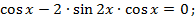
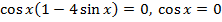или

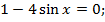
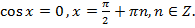
В интервал 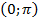попадает лишь значение .

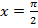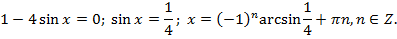
В интервал 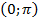попадают значения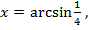

.

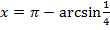Найдем значения функции в критических точках:

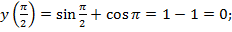
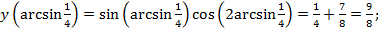
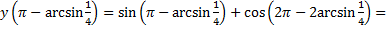
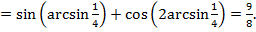
Ответ: среди полученных значений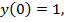

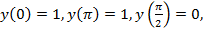
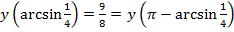наибольшим является 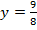, а наименьшим будет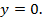

Замечание. При решении примера 2 были использованы формулы: _;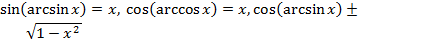

Пример 3. Найти значения, которые может принимать сумма квадратов действительных корней уравнения:

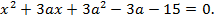
Решение. Квадратное уравнение имеет действительные корни, если его дискриминант больше нуля либо равен нулю.

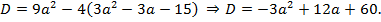
Решим неравенство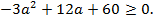

Корнями уравнения 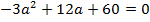или 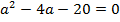являются числа 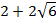и 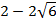. Неравенство 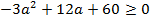выполняется на отрезке

.

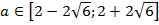Для нахождения суммы квадратов корней уравнения 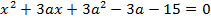воспользуемся теоремой Виета, согласно которой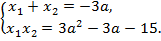

Возведя в квадрат обе части первого уравнения системы, получим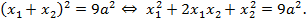

С учетом второго уравнения имеем,

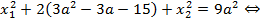
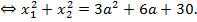
Установим, в каких пределах заключено выражение 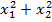, т. е. найдем наибольшее и наименьшее значения функции 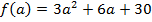на отрезке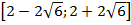

Определим критические точки:

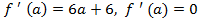при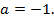

Вычислим значения этой функции на границах отрезка и в критической точке: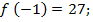

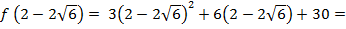
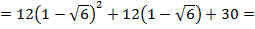
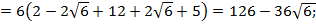
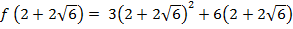+30=

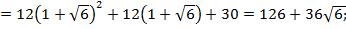
Таким образом, сумма квадратов действительных корней уравнения 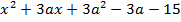=0 может принимать значения, заключенные в интервале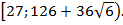

Ответ: .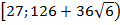

Замечание. В данном примере можно было заметить, что 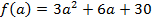представлено в виде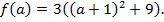

Тогда очевидно, что наименьшим будет значение в точке 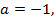а наибольшим (в силу симметрии функции относительно 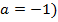– значение в точке .

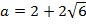При решении текстовых задач на экстремум необходимо «перевести» задачу на язык функций. При этом выбрать неизвестный параметр х и выразить интересующую нас величину как функцию 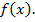После чего найти наибольшее и наименьшее значения этой функции в области ее определения или на указанном отрезке.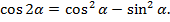

Пример 4. Стороны прямоугольника равны 5 и 10. Через произвольную точку на его меньшей стороне провели прямую, отсекающую прямоугольный треугольник с периметром 12. Найти наименьшее значение площади оставшейся части прямоугольника.

B M   A

С     D

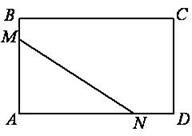
Рис. 6.1. Графическое представление задачи.

Решение. Пусть MN прямая, отсекающая прямоугольный треугольник.

Обозначим AM = x и AN = y (рис. 6.1). Нам необходимо найти наименьшее значение площади S фигуры MBCDN:

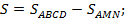
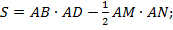
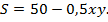
По условию задачи периметр треугольника AMN равен 12, т. е.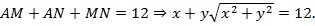

Выразим из данного уравнения y, отделив корень и возведя обе части уравнения в квадрат:

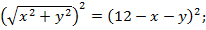
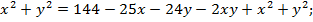
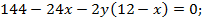
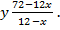
Запишем формулу площади искомой фигуры как функцию от х:

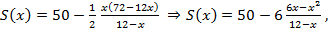
где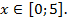

Вычислим производную данной функции:

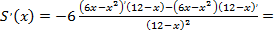
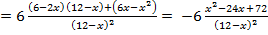
Производная равна нулю, если 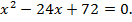Это уравнение имеет два действительных корня:

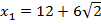и 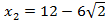, причем 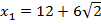не принадлежит заданному интервалу. Получили одну точку 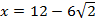, в которой функция имеет минимум, так как при переходе через нее производная меняет знак с минуса на плюс. Других точек экстремума нет, значит, в точке 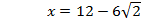функция принимает наименьшее значение. Найдем это значение:

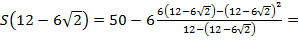
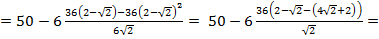
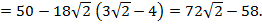
Ответ: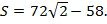

Замечание. Поскольку наименьшее значение площади фигуры MBCDN соответствует наибольшему значению площади треугольника AMN, то задачу можно было решать относительно максимума функции 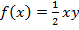на отрезке при 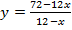.