Элементы векторной алгебры

Высшая математика

Методические указания и задания

для самостоятельной работы

по разделу «Элементы векторной алгебры»

для студентов инженерных и экономических специальностей

Горки

БГСХА

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА

И ПРОДОВОЛЬСТВИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

ГЛАВНОЕ УПРАВЛЕНИЕ ОБРАЗОВАНИЯ, НАУКИ И КАДРОВ

Учреждение образования

«БЕЛОРУССКАЯ ГОСУДАРСТВЕННАЯ

СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ»

Кафедра высшей математики

Высшая математика

Методические указания и задания

Для самостоятельной работы

по разделу «Элементы векторной алгебры»

Для студентов инженерных и экономических специальностей

Горки

БГСХА

УДК 517(072)

ББК 22.1я73

В93

Рекомендовано методической комиссией

мелиоративно-строительного факультета.

Протокол № 7 от 26марта 2012 г.

Авторы:

кандидат технических наук, доцент Е. Н. Крючков;

кандидат технических наук, доцент С. В. Курзенков;

кандидат экономических наук, доцент Т. Б. Воронкова;

ассистент Е. Н. Бобкова;

старший преподаватель Т. В. Левкина

Рецензенты:

кандидат технических наук, доцент В. В. Дятлов;

старший преподаватель И. А. Мазаев

В93	Высшая математика: методические указания и задания для самостоятельной работы по разделу «Элементы векторной алгебры» / Е. Н. Крючков [и др.]. – Горки : БГСХА, 2013. – 74 с.

Приведены краткие теоретические сведения по разделу «Элементы векторной алгебры», тестовые задания, варианты индивидуальных заданий для самостоятельной работы, типовой пример модульного задания и рекомендуемая литература.

Для студентов инженерных и экономических специальностей.

УДК 517(072)

ББК 22.1я73

© УО «Белорусская государственная

сельскохозяйственная академия», 2013

ВВЕДЕНИЕ

Одним из важных моментов учебного процесса является самостоятельная работа студентов. Ее цель состоит в том, чтобы выработать прочные навыки самостоятельной работы с книгой, сформировать умение рационально организовывать свой умственный труд.

Самостоятельная работа студентов по математике способствует лучшему усвоению теоретического материала и методов решения задач.

Предлагаемые методическиеуказания содержаткраткие теоретические сведения по разделу«Элементы векторной алгебры». В разработке знаком «*» помечены те теоретические и практические материалы, которые не обязательны для изучения студентами экономических специальностей, а знаком «**» – студентами инженерных специальностей.

Для того чтобы студенты могли оценить уровень своих знаний по разделу «Элементы векторной алгебры», в данныеуказания включеныконтрольный тест, типовой пример модульного задания, а также трид­цать вариантов индивидуального домашнего задания. После выполнения студентом своего варианта индивидуального задания и проверки преподавателем предполагается его защита. При этомстудент должен показать знание соответствующих теоретических вопросов раздела и приобретенные навыки при решении задач.

Настоящие методические указанияявляются одной из составных частей организационно-методического обеспечения учебного процесса кафедры высшей математики для студентов инженерных и экономических специальностей.

РекомендуемаяЛИТЕРАТУРА

1.Гусак, А. Н. Высшая математика:в 2 ч./ А. Н.Гусак. – Минск: ТетраСистемс, 2000. –Ч.1.

2. Кудрявцев, В. А. Краткий курс высшей математики / В. А. Кудрявцев, Б. П. Демидович.– М.: Наука,1989.

3. Милованов, М.В. Алгебра и аналитическая геометрия: в 2 ч. / М. В. Милованов, Р. И. Тышкевич, А. С. Феденко. – Минск: Вышэйш. шк., 1984. –Ч.1.

4. Письменный, Д. Т. Конспект лекций по высшей математике: в 3 ч./ Д. Т. Пись­менный. – 2-е изд., испр. – М.: Айрис-пресс, 2004. – Ч. 1.

Элементы векторной алгебры

1.1. Векторы, основные понятия

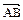Вектором называется направленный отрезок. Вектор с началом в точке А и концом в точке В обозначается символом (или , ,…).

Модулем (длиной) вектора 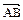называется расстояние от начальной точки А до конечной точки В вектора и обозначается , .

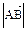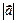Единичным(или ортом) называется вектор 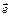, длина которого равна единице.

Нулевым(или нуль-вектором) называется вектор 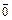, длина которого равна нулю.

Коллинеарными называются векторы и , если они лежат на одной прямой или на параллельных прямых; записывают .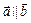

Компланарными называются три вектораи более, если они лежат в одной плоскости или в параллельных плоскостях.

Равными ( 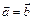)называются два коллинеарных вектора и , если они одинаково направлены и имеют равные длины.

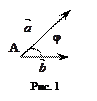Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор 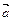имеет бесконечно много векторов, равных ему.

Углом между векторами и называется наименьший угол 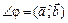, на который нужно повернуть вектор , чтобы его направление совпало с направлением вектора , при условии, что оба вектора отнесены к общему началу, (рис.1).

Угол между векторами измеряется в пределах 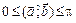. Если угол между векторами 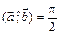(или 90°), то векторы называются ортогональными. В случае, когда 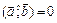(или 0°), говорят, что вектор сонаправлен с вектором , если же 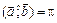(или 180°), то вектор имеет противоположное направление к вектору .

Литература: [ 1, гл. 5, §5.1];[2, гл. 18, § 1, п. 5.6]; [ 3, гл. 2, п. 12.1];[4, гл. 2, § 5].