Элементы векторной алгебры
Векторы и линейные операции над ними
В геометрии вектором называют направленный отрезок 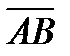 с начальной А и конечной В точками, который можно перемещать параллельно самому себе. Таким образом, считается, что два направленных отрезка
с начальной А и конечной В точками, который можно перемещать параллельно самому себе. Таким образом, считается, что два направленных отрезка 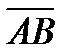 и
и 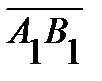 , имеющие равные длины и одно и то же направление, определяют (изображают) один и тот же вектор
, имеющие равные длины и одно и то же направление, определяют (изображают) один и тот же вектор 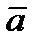 , и пишут
, и пишут 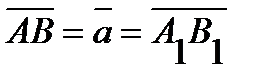 .
.
Длиной (или модулем) 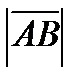 вектора
вектора 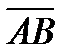 называется число, равное длине отрезка АВ, изображающего вектор.
называется число, равное длине отрезка АВ, изображающего вектор.
Векторы, параллельные одной прямой, называются коллинеарными и компланарными, если они параллельны одной плоскости.
Если вектор 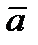 изображается направленным отрезком
изображается направленным отрезком 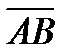 , то вектор, изображаемый направленным отрезком
, то вектор, изображаемый направленным отрезком 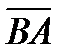 , называется вектором, противоположным вектору
, называется вектором, противоположным вектору 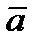 и обозначается -
и обозначается - 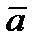 .
.
Для векторов вводятся операции сложения и вычитания. При этом заметим, что знаки «+» и «-», которые ставятся между векторами, имеют другой смысл, чем в алгебре: они обозначают не алгебраическое, а геометрическое сложение векторов по правилу треугольника или параллелограмма.
Произведением вектора 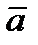 на число
на число 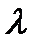 называется вектор
называется вектор 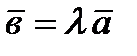 , имеющий длину
, имеющий длину 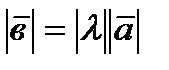
 , направление которого совпадает с направлением вектора
, направление которого совпадает с направлением вектора 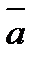 , если
, если 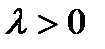 , и противоположно ему, если
, и противоположно ему, если 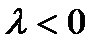 .
.
Сложение векторов и умножение их на число называются линейными операциями над векторами. Эти операции обладают свойствами по форме аналогичными свойствам сложения и умножения чисел.
Если в прямоугольной системе координат точки А и В имеют координаты 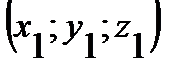 и
и 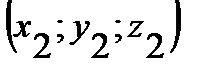 , то координаты вектора
, то координаты вектора 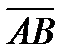 находятся как разности соответствующих координат конца В и начала А этого вектора, т.е.
находятся как разности соответствующих координат конца В и начала А этого вектора, т.е.
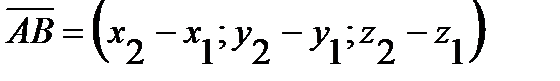 ,
,
а модуль его определяется как расстояние между двумя точками:
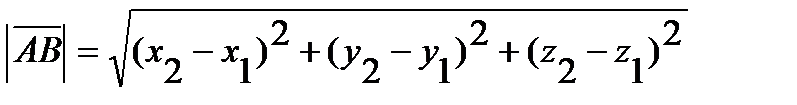 .
.
Линейные операции над векторами, заданными своими координатами 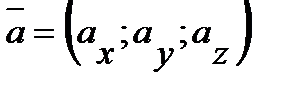 и
и 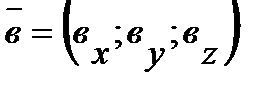 , выполняются по следующим правилам:
, выполняются по следующим правилам:
1) при сложении двух векторов их одноименные координаты складываются: 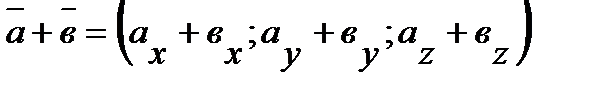 ;
;
2) при умножении вектора 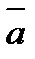 на число
на число 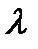 все его координаты умножаются на это число:
все его координаты умножаются на это число: 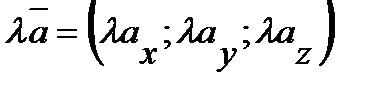 .
.
Два вектора равны, если равны их соответствующие координаты, т.е. 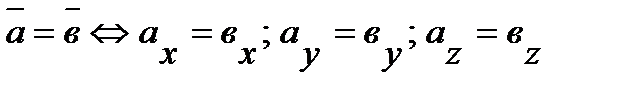 .
.
Два вектора коллинеарные, если их координаты пропорциональны.
Итак, если 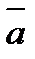 ½½
½½ 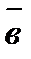 , то
, то 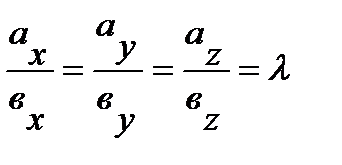 или
или 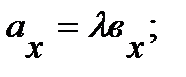
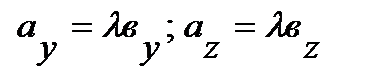 .
.
Умножение векторов
Умножение вектора на вектор бывает двух типов: скалярное и векторное. В результате скалярного умножения двух векторов получаем число (скаляр). В результате векторного произведения двух векторов получаем вектор. Скалярным произведением 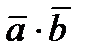 двух ненулевых векторов
двух ненулевых векторов 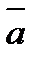 и
и 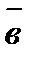 называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними: 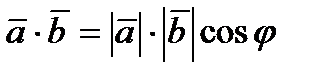 , где
, где 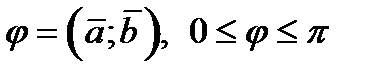 .
.
Свойства скалярного произведения во многом сходны со свойствами произведения действительных чисел.
Векторным произведением двух векторов 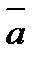 и
и 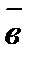 называется вектор
называется вектор 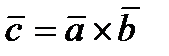 , который:
, который:
1) имеет модуль, численно равный площади параллелограмма, построенного на векторах 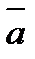 и
и 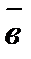 :
: 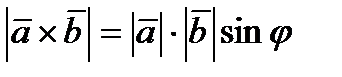 ;
;
2) перпендикулярен к плоскости этого параллелограмма;
3) направлен в такую сторону, с которой кратчайший поворот от 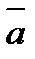 к
к 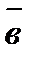 рассматривается совершающимся против часовой стрелки (такое расположение векторов
рассматривается совершающимся против часовой стрелки (такое расположение векторов 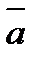 ,
, 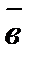 и
и 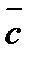 называется правой тройкой векторов).
называется правой тройкой векторов).
Отличительная особенность векторного произведения состоит в том, что для него переместительное свойство (коммутативность) не имеет места. От перестановки векторов – сомножителей векторное произведение изменяет знак на противоположный: 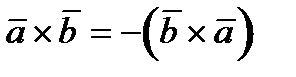 .
.
Три вектора могут быть перемножены несколькими способами. Чаще всего рассматривают смешанное произведение двух векторов векторно и на третий скалярно.В результате получают число.
Смешанное произведение трех векторов 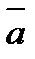 ,
, 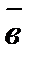 и
и 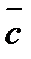 , которое обозначается
, которое обозначается 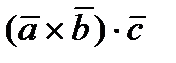 или
или 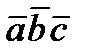 , есть скаляр, абсолютная величина которого равна обьему параллелепипеда, построенного на векторах
, есть скаляр, абсолютная величина которого равна обьему параллелепипеда, построенного на векторах 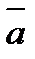 ,
, 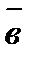 и
и 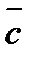 , как на ребрах.
, как на ребрах.
Пусть заданы два вектора 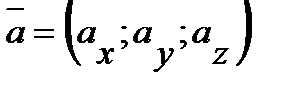 и
и 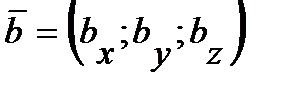 .
.
Скалярное произведение двух ненулевых векторов равно сумме произведений соответствующих координат этих векторов:
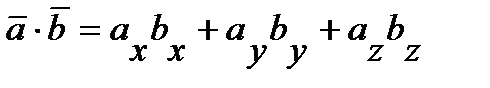 .
.
Угол между векторами вычисляется по формуле
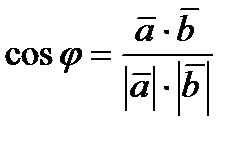 ,
,
или в координатной форме 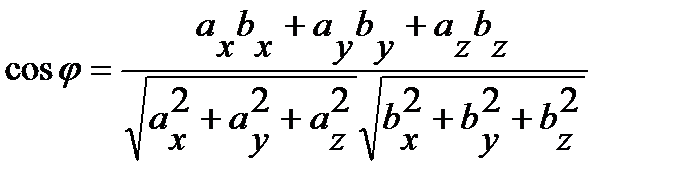 .
.
Условием перпендикулярности ненулевых векторов 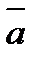 и
и 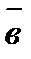 является равенство нулю их скалярного произведения:
является равенство нулю их скалярного произведения:
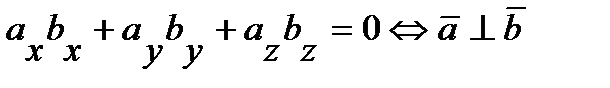 .
.
Векторное произведение ненулевых векторов 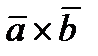 выражается через координаты данных векторов
выражается через координаты данных векторов 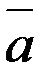 и
и 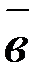 следующим образом:
следующим образом:
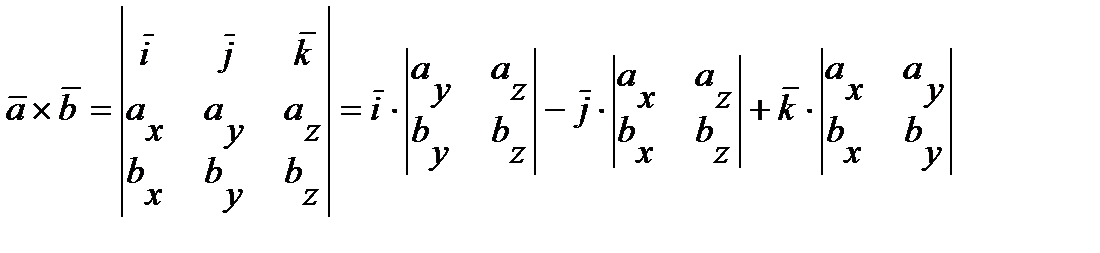 .
.
Равенство нулю векторного произведения двух ненулевых векторов является условием их коллинеарности, т.е. 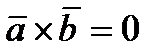
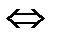
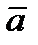 ½½
½½ 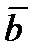 .
.
Скаляр 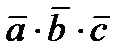 , представляющий смешанное произведение трех векторов, равняется определителю третьего порядка, составленному из координат этих трех векторов:
, представляющий смешанное произведение трех векторов, равняется определителю третьего порядка, составленному из координат этих трех векторов:
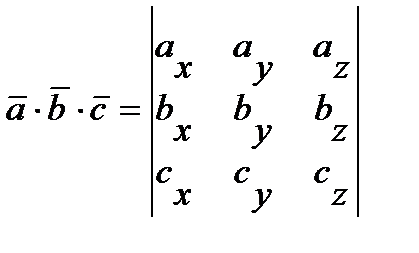 .
.
Равенство нулю смешанного произведения трех ненулевых векторов является условием их компланарности: 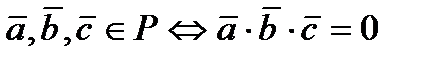 .
.
Задача. Определить внутренние углы 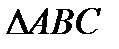 c вершинами
c вершинами 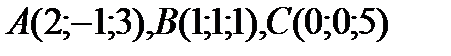 .
.
Решение. Найдем 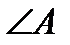 . Для этого надо найти векторы
. Для этого надо найти векторы 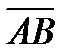 и
и 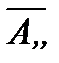 . Зная векторы
. Зная векторы 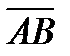 и
и 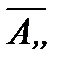 , из формулы (2) получим
, из формулы (2) получим
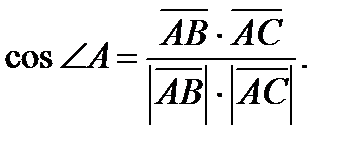
Легко видеть, что 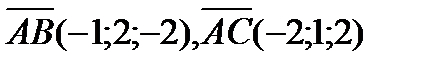 . Тогда
. Тогда
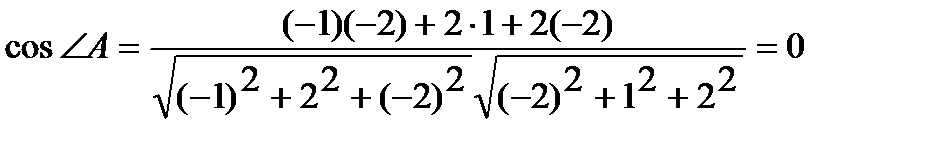 .
.
Отсюда 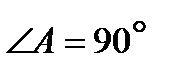 .
.
Аналогично, находя предварительно, что 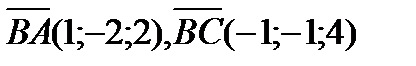 , получим
, получим
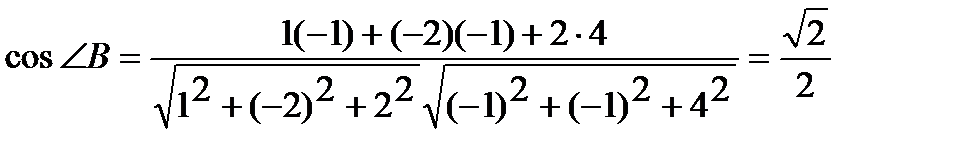 .
.
Отсюда 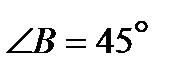 и
и 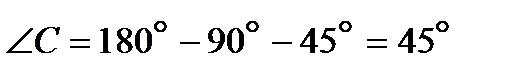 .
.
Задача.Вычислить площадь треугольника с вершинами 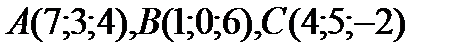 .
.
Решение. Найдем вначале площадь 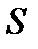 параллелограмма, построенного на векторах
параллелограмма, построенного на векторах 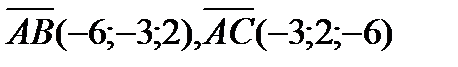 как на сторонах. По определению векторного произведения
как на сторонах. По определению векторного произведения 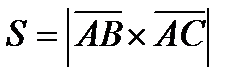 . Но
. Но
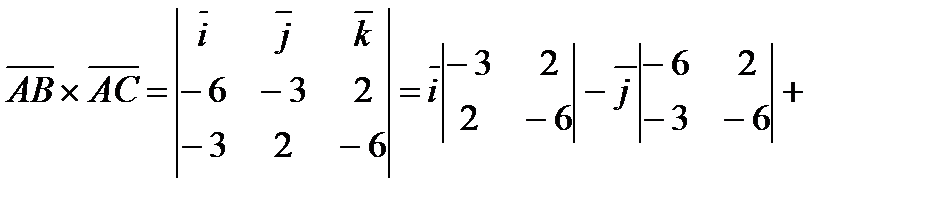
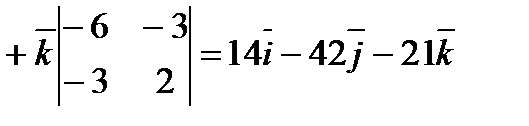 .
.
Тогда 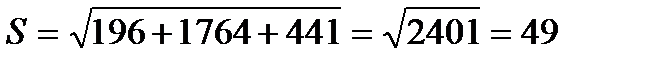 .
.
Следовательно, 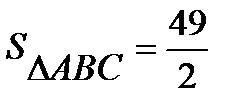 .
.
Задача. Вычислить объем пирамиды с вершинами 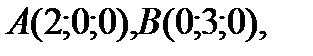
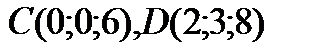 .
.
Решение. Найдем координаты векторов 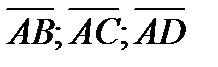 . Очевидно, что
. Очевидно, что 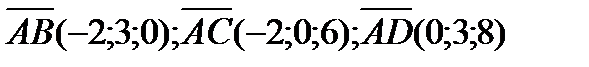 .
.
Тогда 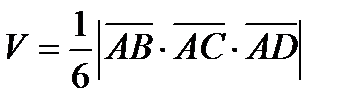 . Но
. Но 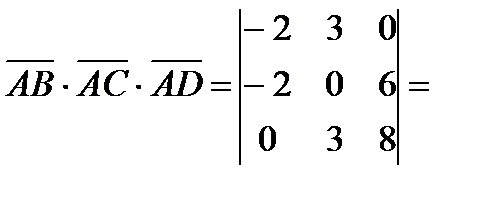
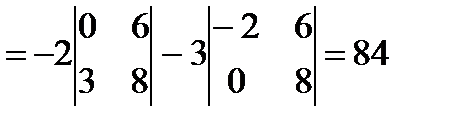 . .
. .
Следовательно, 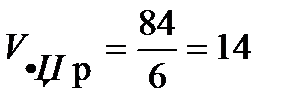 .
.
