I. элементы векторной алгебры
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
(для направления «Прикладная математика и информатика»)
СОДЕРЖАНИЕ
I. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ... 5
1.1. Определение и свойства векторов. 5
1.2. Сложение векторов. 5
1.3. Умножение вектора на действительное число. 7
1.4. Коллинеарные векторы.. 8
1.5. Компланарные векторы.. 8
1.6. Векторные пространства. 9
1.7. Линейная зависимость и независимость векторов. 10
1.8. Базис векторного пространства. Координаты вектора. 11
1.9. Проекция на прямую параллельно данной плоскости. 12
1.10. Проекция вектора на ось. 13
1.11. Ортогональная проекция вектора на ось. 13
1.12. Скалярное произведение векторов. 14
1.13. Метод координат на плоскости и в пространстве. 16
1.14. Векторное произведение векторов. 19
1.15. Смешанное произведение векторов. 21
II. ОБРАЗЫ ПЕРВОЙ СТУПЕНИ.. 23
2.1. Условия, определяющие фигуру в системе координат. 23
2.2. Прямая в аффинной системе координат на плоскости и в пространстве. 24
2.2.1. Уравнения прямой, проходящей через данную точку параллельно данному вектору 24
2.2.2. Уравнения прямой, проходящей через две точки. 25
2.2.3. Общие уравнения прямой. 26
2.2.4. Исследование взаимного расположения прямых. 27
2.3. Прямая в прямоугольной системе координат на плоскости. 29
2.3.1. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору 29
2.3.2. Уравнение прямой, проходящей через данную точку под данным углом к оси (Ох) 30
2.3.3. Нормальное уравнение прямой. 30
2.3.4. Угол между двумя прямыми, заданными общими уравнениями. 31
2.3.5. Угол между наклонными прямыми, заданными уравнениями с угловыми коэффициентами 32
2.3.6. Расстояние от точки до прямой. 33
2.4. Пучок прямых на плоскости. 33
2.5. Геометрический смысл неравенств Ах + Ву + С ³ 0 (£ 0, >0, < 0) 34
2.7. Прямая и плоскость в пространстве. 35
2.7.1. Плоскость в аффинной системе координат.. 35
2.7.1.1. Уравнения плоскости, проходящей через данную точку параллельно двум данным векторам 35
2.7.1.2.. Уравнения плоскости, проходящей через три данные неколлинеарные точки. 36
2.7.1.3. Общее уравнение плоскости. 36
2.7.1.4. Исследование взаимного расположения двух плоскостей. 36
2.7.2. Плоскость и прямая в прямоугольной системе координат.. 38
2.7.2.1. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору 38
2.7.2.2. Угол между двумя плоскостями. 38
2.7.2.3. Угол между прямой и плоскостью.. 39
2.7.2.4. Расстояние от точки до плоскости. 39
2.7.2.5. Расстояние от точки до прямой. 40
2.7.2.6. Расстояние между скрещивающимися прямыми. 40
3. Различные системы координат на плоскости и в пространстве. 42
3.1. Полярная система координат на плоскости. 42
3.2. Цилиндрическая и сферическая системы координат в пространстве. 43
4. ОБРАЗЫ ВТОРОГО ПОРЯДКА.. 43
4.1. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ЛИНИЙ ВТОРОГО ПОРЯДКА.. 43
4.1.1. Окружность. 43
4.1.2. Эллипс. 44
4.1.3. Гипербола. 46
4.1.4. Парабола. 48
4.1.5. Эллипс, гипербола и парабола в полярных координатах. 50
4.2. УПРОЩЕНИЕ УРАВНЕНИЯ ЛИНИИ ВТОРОГО ПОРЯДКА.. 50
4.2.1. Преобразование аффинных координат на плоскости. 51
4.2.2. Преобразование прямоугольных координат.. 51
4.2.3. Преобразование уравнения линии второго порядка при повороте системы координат 52
4.2.4. Упрощение уравнения линии второго порядка. Метрическая классификация линий второго порядка. 53
4.3. ПОВЕРХНОСТИ.. 55
4.3.1. Цилиндрические поверхности. 55
4.3.2. Конические поверхности. 56
4.3.3. Поверхности вращения. 57
4.3.4. Эллипсоид. 58
4.3.5. Однополостный гиперболоид. 59
4.3.6. Двуполостный гиперболоид. 60
4.3.7. Эллиптический параболоид. 61
4.3.8. Гиперболический параболоид. 61
4.3.9. Прямолинейные образующие поверхности. 62
Литература. 64
Основная литература. 64
Дополнительная литература. 64
Методические пособия. 64
I. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
Сложение векторов
Пусть  и и  - любые два вектора. Чтобы к вектору - любые два вектора. Чтобы к вектору  прибавить вектор прибавить вектор  нужно отложить вектор нужно отложить вектор  от любой точки А ( от любой точки А ( 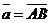 ), от конца В полученного вектора отложить вектор ), от конца В полученного вектора отложить вектор  ( ( 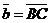 ). Тогда вектор ). Тогда вектор 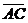 будет вектором суммы, т.е. будет вектором суммы, т.е. 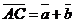 . Иными словами, . Иными словами, 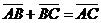 . Свойства сложения векторов. . Свойства сложения векторов. | 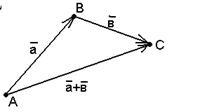 Рис. 2 Рис. 2 |
10. Для любых двух векторов их сумма определена и однозначна. (Следует из определения).
20. 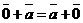 =
=  для любого вектора
для любого вектора  . (Докажите).
. (Докажите).
30. Для любого вектора  существует противоположный вектор (-
существует противоположный вектор (-  ) такой, что
) такой, что  + (-
+ (-  ) =
) = 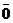 . (Докажите).
. (Докажите).
40. 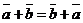 для любых векторов
для любых векторов  и
и  .
.
Доказательство. В случае, когда хотя бы один из векторов нулевой, утверждение следует из предыдущего свойства. Остаётся рассмотреть ненулевые векторы. При этом возможны следующие случаи.
а) Векторы  и и  не параллельны. Пусть не параллельны. Пусть  + +  = = 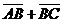 . Отложим от точки А вектор . Отложим от точки А вектор  , пусть , пусть 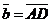 . Так как . Так как 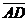 и и 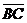 имеют одинаковые длины и направления, то АВСD – параллелограмм. Следовательно, отрезки АВ и DC тоже имеют одинаковые длины и направления. Следовательно, имеют одинаковые длины и направления, то АВСD – параллелограмм. Следовательно, отрезки АВ и DC тоже имеют одинаковые длины и направления. Следовательно, | 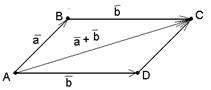 Рис. 3 Рис. 3 |
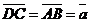 . По правилу сложения векторов
. По правилу сложения векторов 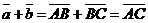 и
и 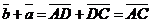 . Отсюда
. Отсюда 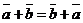 .
.
б) Векторы  и и  параллельны и одинаково направлены (сонаправлены). В этом случае при откладывании от точки А получим параллельны и одинаково направлены (сонаправлены). В этом случае при откладывании от точки А получим 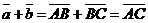 , , 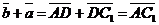 (рис.4). Векторы (рис.4). Векторы 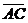 и и 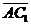 сонаправлены с вектором сонаправлены с вектором  , , |  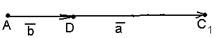 Рис. 4 Рис. 4 |
поэтому сонаправлены между собой. Очевидно, 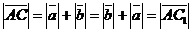 . Следовательно,
. Следовательно, 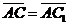 , т.е.
, т.е. 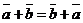 .
.
в) Случай, когда векторы  и
и  параллельны и противоположно направлены, рассмотрите самостоятельно.
параллельны и противоположно направлены, рассмотрите самостоятельно.
Определение 4. Векторы называются коллинеарными, если их можно отложить на одной прямой.
Очевидно, два вектора неколлинеарны тогда и только тогда, когда они ненулевые и не параллельные. Из случая а) проведённого доказательства следует ещё одно правило сложения неколлинеарных векторов:
Чтобы сложить два неколлинеарных вектора, достаточно отложить их от одной точки, построить на них, как на сторонах, параллелограмм, тогда диагональ этого параллелограмма, идущая из данной точки, будет задавать вектор суммы.
50. 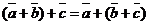 для любых векторов для любых векторов 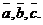 Доказательство. Для левой части получим Доказательство. Для левой части получим 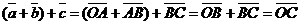 . Для правой части . Для правой части 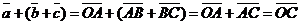 . Результаты равны. . Результаты равны. | 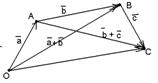 Рис. 5 Рис. 5 |
Определение 5.Разностью упорядоченной пары векторов называется сумма первого вектора и вектора, противоположного второму, т.е.
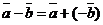 .
.
| Чтобы вычесть из одного вектора второй, достаточно отложить оба вектора от одной точки. Тогда вектор, соединяющий концы полученных отрезков и направленный в сторону уменьшаемого, будет вектором разности (рис. 5). Очевидно, это правило не зависит от того, будут ли векторы коллинеарными или неколлинеарными. Свойства разности: | 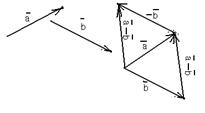 Рис. 6 Рис. 6 |
10. Для любой упорядоченной пары векторов их разность определена и однозначна.
20. Разность двух векторов антикоммутативна.
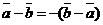 для любых векторов
для любых векторов  и
и  .
.
30. Не выполняется ассоциативный закон, а именно
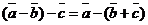 для любых векторов
для любых векторов  ,
,  и
и 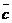 .
.
Задача 1. АВСDA1B1C1D1 - параллелепипед, 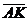 =
= 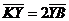 ,
, 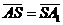 ,
, 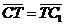 ,
,

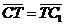 , , 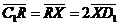 , , 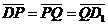 , , 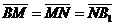 . Найдите 1) . Найдите 1) 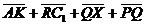 ; 2) ; 2) 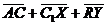 . Решение. 1)Так как . Решение. 1)Так как 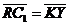 , , 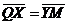 , , 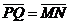 , то , то 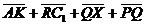 = = 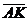 + + 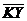 + + 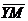 + + 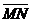 = = 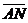 . 2) Так как . 2) Так как 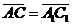 и и 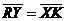 , то , то 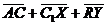 = = 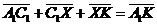 . . | 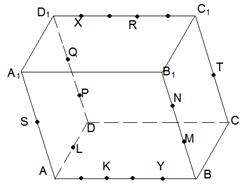 Рис. 7 Рис. 7 |
Коллинеарные векторы
Определение 4. Векторы называются коллинеарными, если их можно отложить на одной прямой.
Свойства коллинеарных векторов.
10. Нулевой вектор коллинеарен с любым вектором.
20. Противоположные векторы коллинеарны.
30. При сложении двух коллинеарных векторов получается вектор, коллинеарный с данными векторами. Следовательно, множество коллинеарных векторов замкнуто относительно операции сложения.
40. Если вектор умножить на действительное число, то получится вектор, коллинеарный данному. Следовательно, множество коллинеарных векторов замкнуто относительно операции умножения на действительное число.
50. Если два вектора коллинеарны, то хотя бы один из них можно представить в виде произведения другого на действительное число.
Доказательство. Пусть векторы  и
и  коллинеарны. Если вектор
коллинеарны. Если вектор  =
= 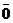 , то
, то  = 0
= 0 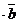 . Если
. Если  =
= 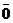 , то
, то  = 0 ×
= 0 ×  . Если
. Если  ¹
¹ 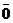 ,
,  ¹
¹ 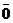 и
и 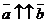 , то
, то  =
= 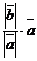 . Если
. Если 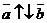 , то
, то  = -
= - 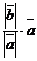 .
.
Из двух последних свойств следуют следующие два свойства.
60. (Необходимое и достаточное условие коллинеарности двух векторов)
Два вектора коллинеарны тогда и только тогда, когда хотя бы один из них можно представить в виде произведения другого на действительное число.
70. Если вектор  не нулевой, то любой вектор, коллинеарный с вектором
не нулевой, то любой вектор, коллинеарный с вектором  , можно представить в виде
, можно представить в виде 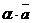 . Иными словами, для задания множества всех коллинеарных векторов достаточно задать один ненулевой из них.
. Иными словами, для задания множества всех коллинеарных векторов достаточно задать один ненулевой из них.
Наконец, из всех приведённых свойств можно сделать вывод, что относительно сложения векторов и умножения вектора на действительное число множество коллинеарных векторов ведёт себя так же как множество всех геометрических векторов.
Задача 2. Отрезок АВ точками С, Р, О, К, М, Т разбит на семь равных частей. Пусть
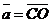 . Выразить через вектор . Выразить через вектор  векторы векторы 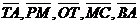 . Решение. . Решение. 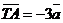 , , 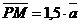 , , 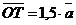 , , 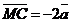 , , | 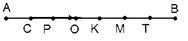 Рис. 8 Рис. 8 |
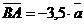 .
.
1.5. Компланарные векторы
Определение 7. Векторы называются компланарными, если их можно отложить в одной плоскости.
Свойства компланарных векторов.
10. Коллинеарные векторы компланарны. Иными словами, во множество всех возможных компланарных между собой векторов вместе с каждым его вектором входят все векторы, коллинеарные с ним. В частности, нулевой вектор содержится в любом таком множестве и вместе с каждым вектором в это множество входит противоположный ему вектор. Отсюда же следует, что множество компланарных векторов замкнуто относительно операции умножения на действительное число.
20. Сумма двух векторов есть вектор, компланарный с ними. Следовательно, множество компланарных векторов замкнуто относительно операции сложения.
30. Три вектора компланарны тогда и только тогда, когда хотя бы один из них можно представить в виде линейной комбинации двух других.
Доказательство. Þ Пусть векторы 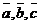 компланарны. Возможны два случая.
компланарны. Возможны два случая.
1) Среди данных векторов есть хотя бы одна пара коллинеарных векторов. Пусть  и
и  коллинеарны. Тогда, по свойствам коллинеарных векторов, хотя бы один из них можно выразить через другой. Пусть
коллинеарны. Тогда, по свойствам коллинеарных векторов, хотя бы один из них можно выразить через другой. Пусть 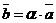 . Тогда
. Тогда 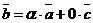 , т.е. вектор
, т.е. вектор  есть линейная комбинация векторов
есть линейная комбинация векторов  и
и 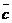 .
.
2) Данные векторы попарно не коллинеарны. Отложим их от одной точки О. Пусть 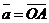 , , 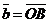 , , 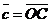 . Отрезки ОА, ОВ, ОС попарно не параллельны. Проведём СD ïïОА так, что D Î ОВ (прямой ОВ). Тогда . Отрезки ОА, ОВ, ОС попарно не параллельны. Проведём СD ïïОА так, что D Î ОВ (прямой ОВ). Тогда 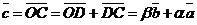 , т.е. вектор , т.е. вектор 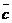 есть линейная комбинация векторов есть линейная комбинация векторов  и и  . . | 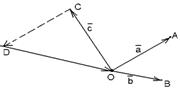 Рис. 9 Рис. 9 |
Ü Пусть 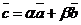 . По свойствам 10 и 20 следует, что вектор
. По свойствам 10 и 20 следует, что вектор 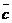 компланарен с векторами
компланарен с векторами  и
и  .
.
40. Если векторы  и
и  не коллинеарны, то любой компланарный с ними вектор можно представить в виде их линейной комбинации.
не коллинеарны, то любой компланарный с ними вектор можно представить в виде их линейной комбинации.
50. Из свойств 10 и 20 следует, что множество всех возможных компланарных векторов относительно операций сложения векторов и умножения вектора на действительное число ведёт себя так же, как множество всех коллинеарных векторов и как множество всех геометрических векторов. Кроме того, для задания множества всех возможных компланарных векторов достаточно задать любые два не коллинеарные из них.
Задача 3. АВСD и AB1C1D1 - два произвольных параллелограмма. Докажите, что
векторы 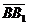 , , 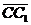 , , 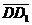 параллельны одной плоскости. Решение. Для решения задачи достаточно показать, что эти векторы компланарны. параллельны одной плоскости. Решение. Для решения задачи достаточно показать, что эти векторы компланарны. 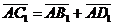 ; ; 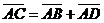 ; ; 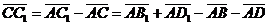 = = ( = = ( 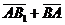 ) + ( ) + ( 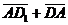 ) = ) = 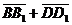 . Так как . Так как 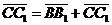 , то эти векторы компланарны . , то эти векторы компланарны . | 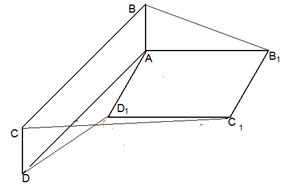 Рис. 10 Рис. 10 |
Векторные пространства
Определение 8. Множество векторов V называется векторным пространством, если в нём определены две алгебраические операции: сложение векторов и умножение вектора на действительное число, удовлетворяющие следующим требованиям:
1. Множество V замкнуто относительно обеих операций.
2. 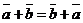 для любых векторов
для любых векторов  и
и  (коммутативный закон сложения).
(коммутативный закон сложения).
3. 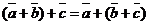 для любых векторов
для любых векторов 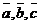 (ассоциативный закон сложения).
(ассоциативный закон сложения).
4. Существует 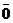 , такой, что
, такой, что 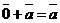 для любого вектора
для любого вектора  .
.
5. Для любого вектора  существует противоположный вектор (-
существует противоположный вектор (-  ) такой, что
) такой, что  + (-
+ (-  ) =
) = 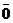 .
.
6. 1 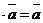 для любого вектора
для любого вектора  .
.
7. 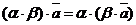 для любого вектора
для любого вектора  и любых действительных чисел a, b.
и любых действительных чисел a, b.
8. 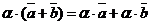 и (
и ( 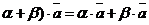 для любых векторов
для любых векторов  ,
,  и любых действительных чисел a, b. (дистрибутивные законы сложения относительно умножения на действительное число).
и любых действительных чисел a, b. (дистрибутивные законы сложения относительно умножения на действительное число).
Примеры векторных пространств (следуют из предыдущего материала).
1. Множество всех геометрических векторов.
2. Множество всех компланарных векторов.
3. Множество всех коллинеарных векторов.
4. Множество, состоящее из одного нулевого вектора.
Проекция вектора на ось
Определение 14. Осью называется прямая с фиксированным на ней единичным вектором. Этот вектор называется ортом оси.
Пусть 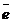 - орт оси, - орт оси, 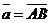 -произвольный вектор, -произвольный вектор, 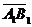 = = 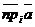 . Так как векторы . Так как векторы 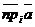 и и 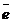 коллинеарны и коллинеарны и 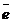 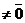 , то , то 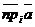 = a× = a× 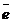 . Число a называется числовой проекцией вектора . Число a называется числовой проекцией вектора  на данную ось и обозначается прl на данную ось и обозначается прl  . Из 70 и 80 свойств векторных проекций следует . Из 70 и 80 свойств векторных проекций следует 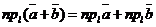 и и 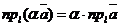 . . | 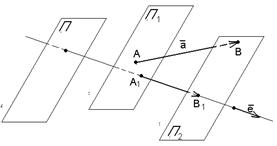 Рис. 15 Рис. 15 |
90. Векторные и числовые проекции вектора на сонаправленные оси параллельно одной и той же плоскости равны. Доказательство. Сонаправленные оси имеют один и тот же орт. Если 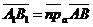 и и 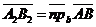 , то , то 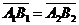 (по свойству отрезков параллельных прямых, заключённых между параллельными плоскостями). Итак, векторные (по свойству отрезков параллельных прямых, заключённых между параллельными плоскостями). Итак, векторные | 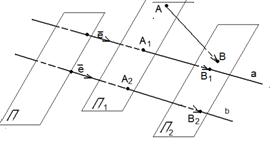 Рис. 16 Рис. 16 |
Проекции вектора на сонаправленные оси равны. Так как у этих осей один и тот же орт, то числовые проекции тоже равны.
100. Так как направление оси можно задавать любым ненулевым вектором, сонаправленным с ортом оси, то можно говорить о проекции одного вектора на направление другого и обозначать 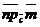 ( проекция вектора
( проекция вектора 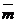 на направление вектора
на направление вектора 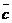 параллельно плоскости П).
параллельно плоскости П).
II. ОБРАЗЫ ПЕРВОЙ СТУПЕНИ
Общие уравнения прямой
Из уравнений (16) и (18) видно, что любую прямую на плоскости можно задать уравнением первой степени с двумя переменными. Возникает обратный вопрос: всякое ли уравнение первой степени с двумя переменными задаёт в аффинной системе координат на плоскости некоторую прямую? Аналогично, уравнения (161) и (181) эквивалентны системе двух независимых уравнений первой степени с тремя переменными. Поэтому возникает обратная задача: Любая ли система двух независимых уравнений первой степени с тремя переменными задаёт в аффинной системе координат в пространстве прямую?
I.Общее уравнение прямой на плоскости
Дано: R = 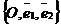 и уравнение Ах + Ву + С = 0, где из коэффициентов А и В хотя бы один отличен от нуля.
и уравнение Ах + Ву + С = 0, где из коэффициентов А и В хотя бы один отличен от нуля.
Показать, что данное уравнение определяет прямую.
Доказательство. Пусть В ¹ 0. При х0 = 0 из данного уравнения получаем у0 = 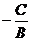 . Вектор
. Вектор 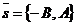 не нулевой, поэтому существует и только одна прямая l такая, что l ' М0, где М0(х0, у0) и l ½½
не нулевой, поэтому существует и только одна прямая l такая, что l ' М0, где М0(х0, у0) и l ½½  . Запишем уравнение l, используя (16). Получим
. Запишем уравнение l, используя (16). Получим 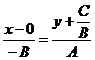 . После преобразования Ах + Ву + С = 0. Получили данное уравнение. Следовательно, оно задаёт прямую.
. После преобразования Ах + Ву + С = 0. Получили данное уравнение. Следовательно, оно задаёт прямую.
Уравнение Ах + Ву + С = 0 называется общее уравнение прямой на плоскости. При этом из доказательства следует, что вектор 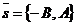 параллелен этой прямой.
параллелен этой прямой.
Нормальное уравнение прямой
Дано: R = 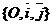 , , 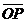 : : 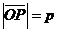 , , 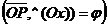 , l ' Р, l ^ , l ' Р, l ^ 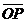 . Найти уравнение l. М Î l Û пр . Найти уравнение l. М Î l Û пр 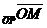 = р. Отсюда М Î l Û = р. Отсюда М Î l Û 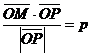 . Так как . Так как 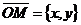 , , 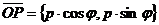 , то , то | 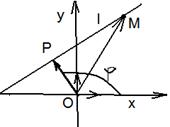 Рис. 37 Рис. 37 |
М Î l Û 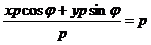 . Отсюда М Î l Û
. Отсюда М Î l Û 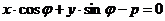 (30)
(30)
Уравнение (30) называется нормальное уравнение прямой. В этом уравнении
(cosj)2 + (sinj)2 = 1, свободный член (-р) £ 0.
Очевидно, нормальное уравнение прямой является одним из общих её уравнений. Если прямая задана в аффинной системе координат уравнением Ax + By + C = 0, то все остальные её общие уравнения имеют вид lAx + lBy + lC = 0, где l ¹ 0 (*). Следовательно, существует такое l, при котором уравнение (*) будет нормальным уравнением данной прямой. Для этого должны выполняться условия (lА)2 + (lВ)2 = 1, (lС) £ 0. Отсюда 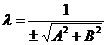 и знак перед корнем должен быть противоположен знаку С. (Если С = 0, то знак можно взять любой). Коэффициент
и знак перед корнем должен быть противоположен знаку С. (Если С = 0, то знак можно взять любой). Коэффициент 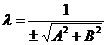 называется нормирующим множителем, а уравнение
называется нормирующим множителем, а уравнение 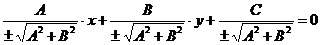 будет нормальным уравнением данной прямой. Говорят, что уравнение Ax + By + C = 0 приведено к нормальному виду.
будет нормальным уравнением данной прямой. Говорят, что уравнение Ax + By + C = 0 приведено к нормальному виду.
Пучок прямых на плоскости
Определение 24. Пучком прямых на плоскости называется множество всех прямых этой плоскости, проходящих через одну точку. Эта точка называется центром пучка.
Пучок можно задать двумя способами: центром и парой пересекающихся прямых. I.Пучок задан центром. Дано.R = 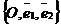 , С(х0, у0) – центр пучка (рис. 43). Найти условие, определяющее пучок. Решение. Прямая l принадлежит пучку с центром С тогда и , С(х0, у0) – центр пучка (рис. 43). Найти условие, определяющее пучок. Решение. Прямая l принадлежит пучку с центром С тогда и | 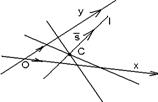 Рис. 43 Рис. 43 |
только тогда, когда l ' С. При этом направляющим вектором может быть любой ненулевой вектор 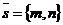 . Следовательно, l принадлежит пучку Û l :
. Следовательно, l принадлежит пучку Û l : 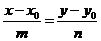 , где m, n – любые действительные числа, не равные одновременно нулю. Итак, пучок с центром С задаётся уравнением
, где m, n – любые действительные числа, не равные одновременно нулю. Итак, пучок с центром С задаётся уравнением 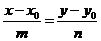 (36).
(36).
В уравнении (36) две пары переменных. Меняя m, n, мы будем получать все возможные прямые пучка. Если m, n зафиксированы, то зафиксирована прямая пучка. При этом, меняя х, у, мы будем получать все возможные точки на полученной прямой.
2. Пучок задан парой пересекающихся прямых. Дано.R = 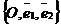 , l1 : A1x + B1y + C1 = 0, l2 : A2x + B2y + C2 = 0 (рис. 44). Найти уравнение пучка. Решение. Пусть l1 Ç l2 = С и С(х0, у0). Точка С будет центром пучка. Используя уравнение (36) получим, что прямая l принадлежит пучку Û l : , l1 : A1x + B1y + C1 = 0, l2 : A2x + B2y + C2 = 0 (рис. 44). Найти уравнение пучка. Решение. Пусть l1 Ç l2 = С и С(х0, у0). Точка С будет центром пучка. Используя уравнение (36) получим, что прямая l принадлежит пучку Û l : 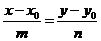 . Здесь . Здесь | 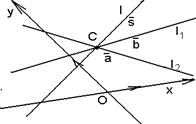 Рис. 44 Рис. 44 |
вектор 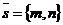 - любой ненулевой вектор. Из уравнений прямых l1 и l2 векторы
- любой ненулевой вектор. Из уравнений прямых l1 и l2 векторы 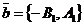 и
и 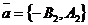 параллельны прямым l1 и l2 соответственно, поэтому они не коллинеарны. Следовательно, любой вектор
параллельны прямым l1 и l2 соответственно, поэтому они не коллинеарны. Следовательно, любой вектор 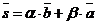 , где a, b - любые действительные числа, не равные нулю одновременно. Отсюда
, где a, b - любые действительные числа, не равные нулю одновременно. Отсюда 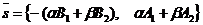 . Уравнение (36) перепишется
. Уравнение (36) перепишется 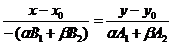 . После преобразования получим:
. После преобразования получим:
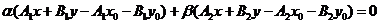 (*).
(*).
Так как С = l1 Ç l2, то A1x0 + B1y0 + C1 = 0 и A2x0 + B2y0 + C2 = 0. Отсюда -( A1x0 + B1y0) = С1, -( A2x0 + B2y0) = 0. Подставив в (*), получим уравнение данного пучка
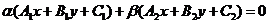 (37)
(37)
В уравнении (37) тоже две пары переменных (a, b) и (х, у).
Задача 15. Дано: R = 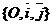 , l1 : 3х + 4у +12 = 0, l2 : 4х + 3у - 24 = 0, l3 : х + 2у + 3 = 0.
, l1 : 3х + 4у +12 = 0, l2 : 4х + 3у - 24 = 0, l3 : х + 2у + 3 = 0.
Найти уравнение прямой l, Если l ' (l1 Ç l2) и l ^ l3.
Решение. Так как l ' (l1 Ç l2), то l принадлежит пучку прямых, определяемому прямыми l1 и l2. Следовательно, уравнение l можно искать в виде
a(3х + 4у +12 ) + b(4х + 3у - 24) = 0 (*)
Преобразовав это уравнение, получим (3a + 4b)х + (4a +3b)у + (12a - 24b) = 0 (**).
Используем условие перпендикулярности прямых (33). Получим 1×(3a + 4b) + 2×(4a +3b) = 0, или 11a + 10b = 0. Так как все решения этого уравнения пропорциональны, а уравнение (*) при пропорциональных парах (a, b) задаёт одну и ту же прямую, то достаточно найти одну ненулевую пару (a, b). При a = 10 b = -11. Подставив в (**), получим уравнение
l : 14х - 4у - 384 = 0.
2.5. Геометрический смысл неравенств Ах + Ву + С ³ 0 (£ 0, >0, < 0)
Дано. R = 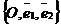 , Ах + Ву + С ³ 0 (А и В н равны нулю одновременно) (38).
, Ах + Ву + С ³ 0 (А и В н равны нулю одновременно) (38).
Исследовать, какую фигуру задаёт неравенство (38). Решение. Пусть l : Ах + Ву + С = 0. Если бы вектор 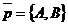 был параллелен прямой l, то векторы был параллелен прямой l, то векторы 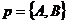 и и 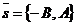 были бы коллинеарны. Но тогда были бы коллинеарны. Но тогда 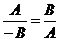 . Отсюда А2 + В2 = 0, т.е. . Отсюда А2 + В2 = 0, т.е. | 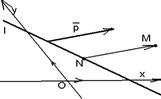 Рис. 45 Рис. 45 |
А = В = 0, что противоречит условию. Итак, вектор 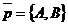 не параллелен прямой (рис.45).
не параллелен прямой (рис.45).
Рассмотрим множество всех точек плоскости, не лежащих на прямой l. Пусть М – любая из них. Пусть 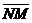 параллелен
параллелен 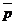 , где N Î l. Тогда
, где N Î l. Тогда 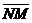 =
= 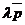 . При этом l > 0 Û точки М лежат в одной открытой полуплоскости с границей l, а именно в той в сторону которой направлен вектор
. При этом l > 0 Û точки М лежат в одной открытой полуплоскости с границей l, а именно в той в сторону которой направлен вектор 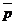 . Перепишем последнее равенство в координатах. Если М (х, у), N (х0 , у0), то х - х0 = lА, у - у0 = lВ. Отсюда х0 = х - lА, у0 = у - lВ. Так как N Î l, то Ах0 + Ву0 + С = 0. Следовательно, А(х - lА) + В(у - lВ) + С = 0. Отсюда Ах + Ву + С = l (А2 + В2). Так как А2 + В2 > 0, то знак трёхчлена Ах + Ву + С совпадает со знаком l . Итак, Ах + Ву + С > 0 Û точка М (х, у) лежит в открытой полуплоскости с границей l, а именно в той, в сторону которой направлен вектор
. Перепишем последнее равенство в координатах. Если М (х, у), N (х0 , у0), то х - х0 = lА, у - у0 = lВ. Отсюда х0 = х - lА, у0 = у - lВ. Так как N Î l, то Ах0 + Ву0 + С = 0. Следовательно, А(х - lА) + В(у - lВ) + С = 0. Отсюда Ах + Ву + С = l (А2 + В2). Так как А2 + В2 > 0, то знак трёхчлена Ах + Ву + С совпадает со знаком l . Итак, Ах + Ву + С > 0 Û точка М (х, у) лежит в открытой полуплоскости с границей l, а именно в той, в сторону которой направлен вектор 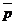 . Неравенство Ах + Ву + С ³ 0 задаёт эту полуплоскость вместе с границей.
. Неравенство Ах + Ву + С ³ 0 задаёт эту полуплоскость вместе с границей.
Общее уравнение плоскости
Если в уравнениях (39) или (44) раскрыть определители, то получим уравнение первой степени с тремя переменными, следовательно, в аффинной системе координат всякая плоскость может быть задана некоторым уравнением вида Ах + Ву + Сz + D = 0. Поставим обратную задачу: всякое ли уравнение вида Ах + Ву + Сz + D = 0 задаёт в аффинной системе координат некоторую плоскость.
Дано: R = 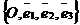 , Ах + Ву + Сz + D = 0 (45), где коэффициенты А, В, С не все равны нулю.
, Ах + Ву + Сz + D = 0 (45), где коэффициенты А, В, С не все равны нулю.
Доказать: уравнение (45) задаёт плоскость.
Доказательство. Проведём доказательство, предполагая, что А ¹ 0. Если y = z = 0, то 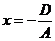 . Следовательно, координаты точки М0 (
. Следовательно, координаты точки М0 ( 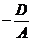 , 0, 0) удовлетворяют уравнению (45), т.е. если плоскость существует, то она обязательно пройдёт через эту точку. Векторы
, 0, 0) удовлетворяют уравнению (45), т.е. если плоскость существует, то она обязательно пройдёт через эту точку. Векторы 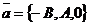 и
и 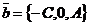 , очевидно, не коллинеарны. Используя (39), составим уравнение плоскости, проходящей через точку М0 параллельно векторам
, очевидно, не коллинеарны. Используя (39), составим уравнение плоскости, проходящей через точку М0 параллельно векторам  и
и  . Получим
. Получим
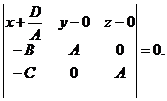 После упрощения: Ах + Ву + Сz + D = 0, т.е. данное уравнение. Итак, (45) действительно задаёт плоскость.
После упрощения: Ах + Ву + Сz + D = 0, т.е. данное уравнение. Итак, (45) действительно задаёт плоскость.
Уравнение (45) называется общее уравнение плоскости.
Следствие. Если плоскость задана общим уравнением (45), то из векторов 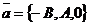 ,
, 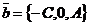 и
и 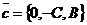 хотя бы два отличны от
хотя бы два отличны от 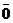 и неколлинеарны. Любой ненулевой вектор из них параллелен данной плоскости.
и неколлинеарны. Любой ненулевой вектор из них параллелен данной плоскости.
ОБРАЗЫ ВТОРОГО ПОРЯДКА
Окружность
Определение 26. Окружностьюс центром С и радиусом а называется множество точек плоскости, удалённых от точки С на расстояние а. Обозначение w = окр(С, а).
Если на плоскости зафиксирована ПДСК и С(х0,у0), то М Î w Û êСМê = а. Если М(х, у), то М Î w Û 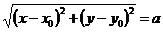 Û (х – х0)2 + (у – у0)2 = а2. Следовательно, уравнение окружности в ПДСК есть (х – х0)2 + (у – у0)2 = а2.
Û (х – х0)2 + (у – у0)2 = а2. Следовательно, уравнение окружности в ПДСК есть (х – х0)2 + (у – у0)2 = а2.
Если А(х1, у1) Î w, то уравнение касательной к w в точке А можно получить как уравнение прямой, проходящей через точку А перпендикулярно вектору 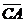 ={
={
