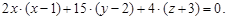Частные производные и дифференциалы высших порядков

Частными производными второго порядка называют частные производные, взятые от частных производных первого порядка

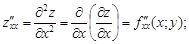
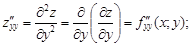
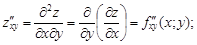
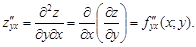
Аналогично определяются частные производные третьего и более высоких порядков. Запись 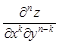означает, что функция z k раз продифференцирована по переменной x и 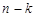раз по переменной y.

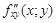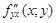Частные производные и называются смешанными. Значения смешанных производных равны в тех точках, в которых эти производные непрерывны.

Полный дифференциал второго порядка d ²z функции z = f(x; y) выражается формулой

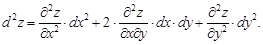
Дифференциалы высших порядков определяются по аналогии

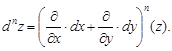
Пример 13.Найти частные производные второго порядка функции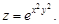

Решение

Вначале найдем частные производные первого порядка

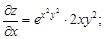
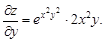
Продифференцировав их еще раз, получим

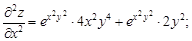
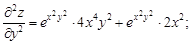
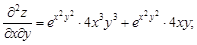
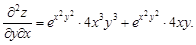
Сравнивая последние два выражения, видим, что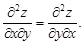

Пример 14. Найти полный дифференциал второгопорядка функции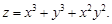

Решение

Находим частные производные второго порядка

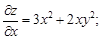
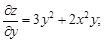
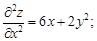
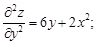
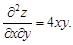
Следовательно,

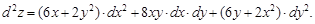
Тест 9.Частная производная второго порядка 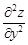функции 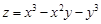равна:

1)

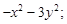
2)

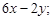
3)

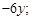
4)

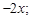
5)

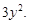
Тест 10.Частная производная второго порядка 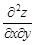функции
z = 7x²y – 4y² равна:

1)0;

2) 14xy;

3) 14x;

4) 7x²y;

5) –8y.

Касательная плоскость и нормаль к поверхности

Пусть M₀(x₀; y₀; z₀) – фиксированная точка на поверхности, заданной функцией z = f(x; y) или уравнением F(x; y; z) = 0.

Касательной плоскостью к поверхности в точке M₀ называется плоскость, в которой расположены касательные к всевозможным кривым, проведенным на поверхности через точку M₀.

Нормалью называется прямая, проходящая через точку M₀ перпендикулярно касательной плоскости.

Из определений следует, что нормальный вектор касательной плоскости и направляющий вектор нормали совпадают.

Если поверхность задана уравнением z = f(x; y), то уравнение касательной плоскости в точке M₀(x₀; y₀; z₀) к данной поверхности имеет вид

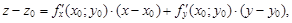(1)

а канонические уравнения нормали, проведенной через точку M₀(x₀; y₀; z₀) поверхности, имеют вид

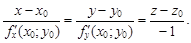(2)

В случае, когда уравнение гладкой поверхности задано в неявном виде: F(x; y; z) = 0 и F(x₀; y₀; z₀) = 0, то уравнение касательной плоскости в точке M₀(x₀; y₀; z₀) имеет вид

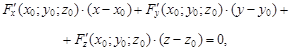(3)

а уравнение нормали

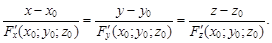(4)

Пример 15. Найти уравнение касательной плоскости и уравнения нормали к поверхности 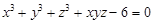в точке M₀(1; 2; –1).

Решение

Вычисляем значения частных производных в точке M₀(1; 2; –1)

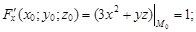
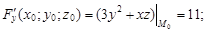
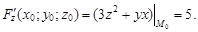
Подставляя их в уравнения (3) и (4), получаем соответственно уравнение касательной плоскости: 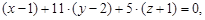канонические уравнения нормали: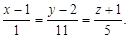

Тест 11.Уравнение касательной плоскости к поверхности 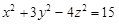в точке P₀(2; –3; 2) имеет следующий вид:

1)

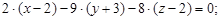
2)

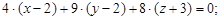
3)

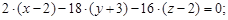
4)

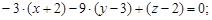
5)