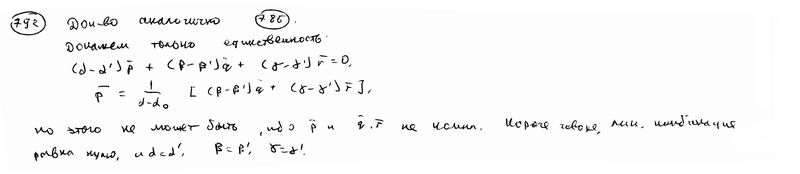| | | Определить координаты точки М, если ее радиус-вектор составляет с координатными осями одинаковые углы и его модуль равен 3.  Глава 30. Линейные операции над векторами Глава 30. Линейные операции над векторами | 761 | | По данным векторам  и и  построить каждый из следующих векторов: 1). построить каждый из следующих векторов: 1).  , 2). , 2). 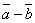 , 3). , 3). 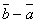 , 4). , 4). 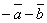 . .  | | 762 | | Даны 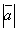 =13, =13, 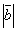 =19 и =19 и 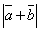 =24. Вычислить =24. Вычислить 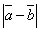 . . 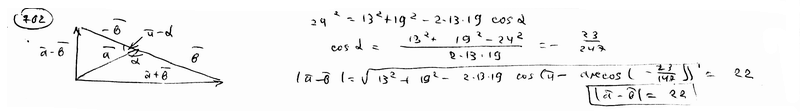 | | 763 | | Даны 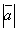 =11, =11, 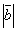 =23 и =23 и 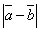 =30. Определить =30. Определить 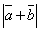 . . 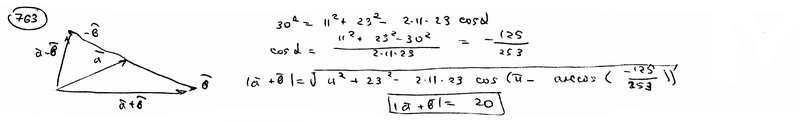 | | 764 | | Векторы  и и 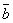 взаимно перпендикулярны, причем взаимно перпендикулярны, причем 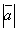 =5, =5, 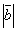 =12. Определить =12. Определить 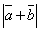 и и 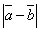 . . 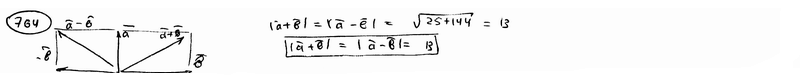 | | 765 | | Векторы  и и 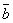 образуют угол образуют угол 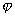 =600, причем =600, причем 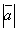 =5 и =5 и 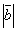 =8. Определить =8. Определить 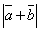 и и 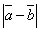 . . 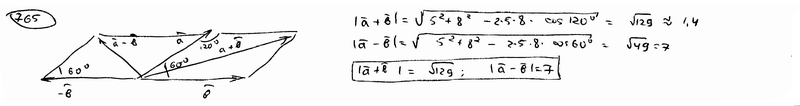 | | 766 | | Векторы  и и 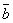 образуют угол образуют угол 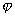 =1200, причем =1200, причем 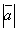 =3 и =3 и 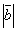 =5. Определить =5. Определить 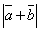 и и 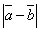 . . 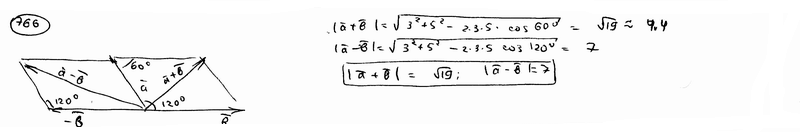 | | 767 | | Какому условию должны удовлетворять векторы  и и 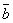 , чтобы имели место следующие соотношения: , чтобы имели место следующие соотношения: | | | 767.1 | 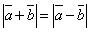 ; ; | | | 767.2 | 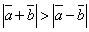 ; ; | | | 767.3 |  . .  | | 768 | | Какому условию должны удовлетворять векторы  и и 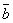 , чтобы вектор , чтобы вектор 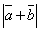 делил пополам угол между векторами делил пополам угол между векторами  и и  . .  | | 769 | | По данным векторам  и и  построить каждый из следующих векторов: построить каждый из следующих векторов: | | | 769.1 |  ; ; | | | 769.2 |  ; ; | | | 769.3 | 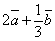 ; ; | | | 769.4 | 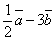 . .  | | 770 | | В треугольнике АВС вектор 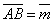 и вектор и вектор 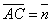 . Построить каждый из следующих векторов. Принимая в качестве масштабной единицы . Построить каждый из следующих векторов. Принимая в качестве масштабной единицы 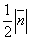 , построить также векторы: , построить также векторы: | | | 770.1 | 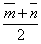 ; ; | | | 770.2 | 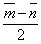 ; ; | | | 770.3 | 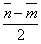 ; ; | | | 770.4 | 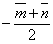 ; ; | | | 770.5 | 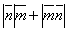 ; ; | | | 770.6 | 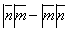 . . 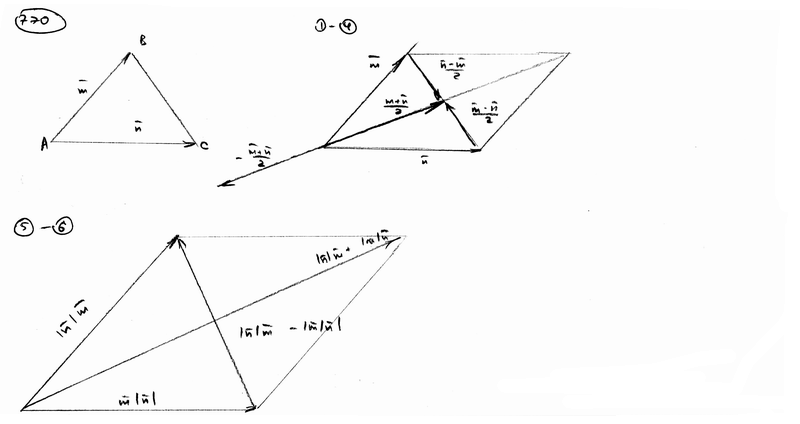 | | 771 | | Точка О является центром масс треугольника АВС. Доказать, что 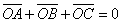 . . 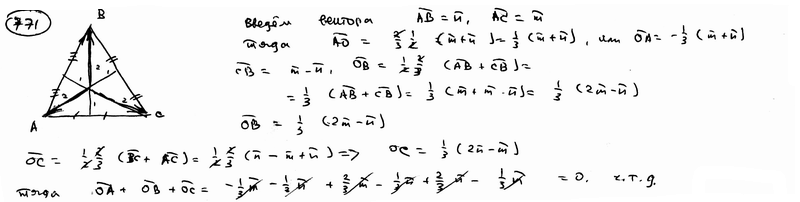 | | 772 | | В правильном пятиугольнике ABCDE заданы векторы, совпадающие с его ребрами: 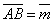 , , 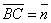 , , 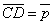 , , 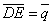 , , 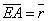 . Построить векторы: . Построить векторы: | | | 772.1 | 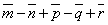 ; ; | | | 772.2 | 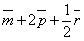 ; ; | | | 772.3 | 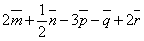 . . 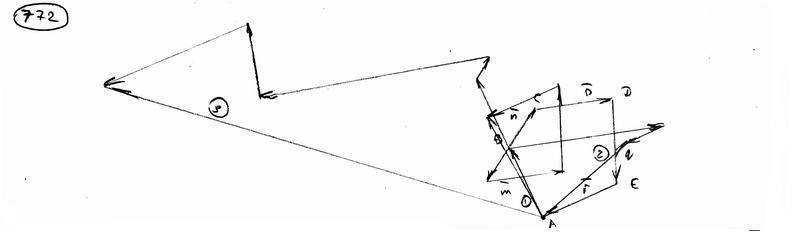 | | 773 | | В параллелепипеде ABCDA’B’C’D’ (рис.) заданы векторы, совпадающие с его ребрами: 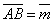 , , 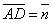 , , 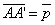 . Построить каждый из следующих векторов: . Построить каждый из следующих векторов: 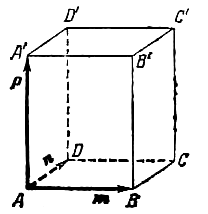 | | | 773.1 | 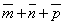 ; ; | | | 773.2 | 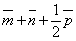 ; ; | | | 773.3 | 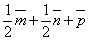 ; ; | | | 773.4 | 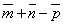 ; ; | | | 773.5 | 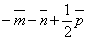 . . 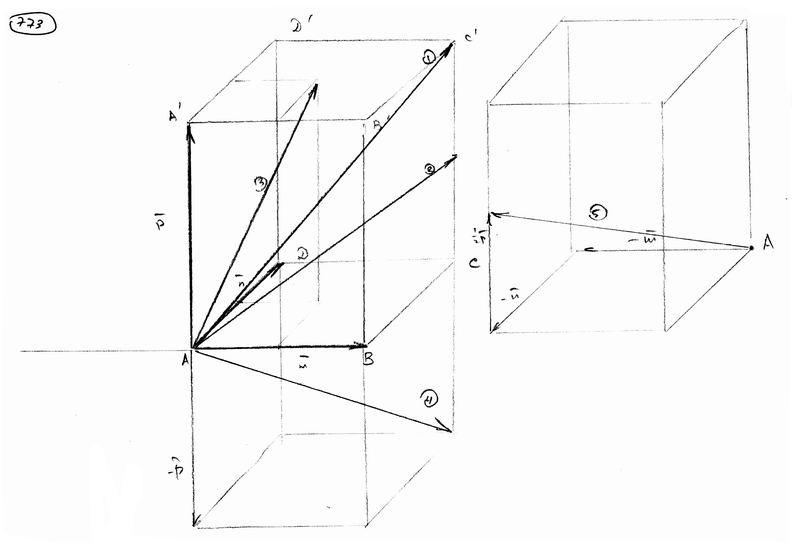 | | 774 | | Три силы 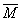 , , 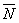 , , 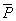 , приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину их равнодействующей , приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину их равнодействующей 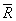 , если известно, что , если известно, что 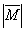 =2Н, =2Н,  =10Н, =10Н, 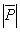 =11Н. =11Н. 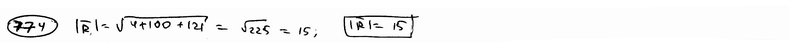 | | 775 | | Даны два вектора  ={3; -2; 6}, ={3; -2; 6}, 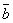 ={-2; 1; 0}. Определить проекции на координатные оси следующих векторов: ={-2; 1; 0}. Определить проекции на координатные оси следующих векторов: | | | 775.1 | 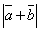 ; ; | | | 775.2 | 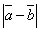 ; ; | | | 775.3 |  ; ; | | | 775.4 |  ; ; | | | 775.5 |  ; ; | | | 775.6 |  . .  | | 776 | | Проверить коллинеарность векторов  ={2; -1; 3} и ={2; -1; 3} и  ={-6; 3; -9}. Установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны. ={-6; 3; -9}. Установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны.  | | 777 | | Определить, при каких значениях  , , 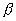 векторы векторы 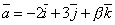 и и 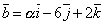 коллинеарны. коллинеарны. 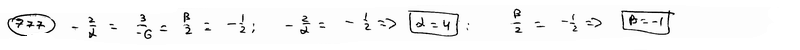 | | 778 | | Проверить, что четыре точки A(3; -1; 2), B(1; 2; -1), C(2; 2; -7), D(3; -5; 3) служат вершинами трапеции.  | | 779 | | Даны точки A(-1; 5; -10}, B(5; -7; 8), C(2; 2; -7), D(5; -4; 2). Проверить, что векторы  и и  коллинеарны, установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны. коллинеарны, установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны.  | | 780 | | Найти орт вектора  ={6; -2; -3}. ={6; -2; -3}.  | | 781 | | Найти орт вектора  ={3; 4; -12}. ={3; 4; -12}. 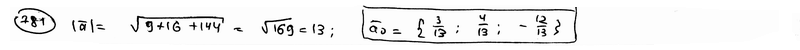 | | 782 | | Определить модули суммы и разности векторов  ={3; -5; 8} и ={3; -5; 8} и  ={-1; 1; -4}. ={-1; 1; -4}.  | | 783 | | Дано разложение вектора  по базису по базису 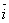 , , 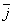 , , 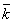 : : 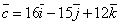 . Определить разложение по этому же базису вектора . Определить разложение по этому же базису вектора 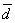 , параллельного вектору , параллельного вектору 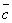 и противоположного с ним направления, при условии, что и противоположного с ним направления, при условии, что 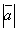 =75. =75.  | | 784 | | Два вектора  ={2; -3; 6} и ={2; -3; 6} и 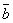 ={-1; 2; -2} приложены к одной точке. Определить координаты вектора ={-1; 2; -2} приложены к одной точке. Определить координаты вектора  направленного по биссектрисе угла между векторами направленного по биссектрисе угла между векторами  и и  , при условии, что , при условии, что  . .  | | 785 | | Векторы 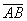 ={2; 6; -4} и ={2; 6; -4} и 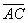 ={4; 2; -2} совпадают со сторонами теругольника АВС. Определить координаты векторов, приложенных к вершинам треугольника и совпадающими с его медианами AM, BN, CP. ={4; 2; -2} совпадают со сторонами теругольника АВС. Определить координаты векторов, приложенных к вершинам треугольника и совпадающими с его медианами AM, BN, CP. 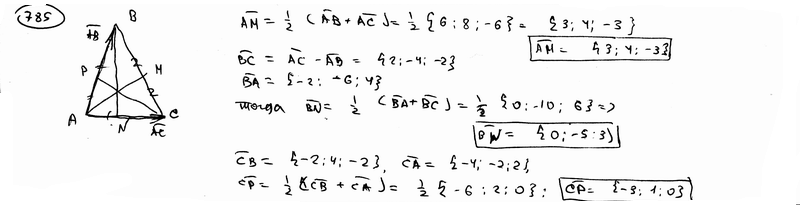 | | 786 | | Доказать, что если 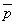 и и 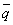 - какие угодно неколлинеарные векторы, то всякий вектор, лежащих в их плоскости, может быть представлен в виде - какие угодно неколлинеарные векторы, то всякий вектор, лежащих в их плоскости, может быть представлен в виде 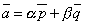 . Доказать, что числа . Доказать, что числа  и и  однозначно определяются векторами однозначно определяются векторами  , , 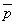 и и 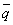 . .  | | 787 | | На плоскостиданы два вектора  ={2; -3}, ={2; -3},  ={1; 2}. Найи разложение вектора ={1; 2}. Найи разложение вектора  ={9; 4} по базису ={9; 4} по базису  , ,  . .  | | 788 | | На плоскости даны три вектора  ={3; -2}, ={3; -2},  ={-2; 1}, ={-2; 1}, 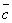 ={7; -4}. Определить разложение каждого из этих трех векторов, принимая в качестве базиса два других. ={7; -4}. Определить разложение каждого из этих трех векторов, принимая в качестве базиса два других. 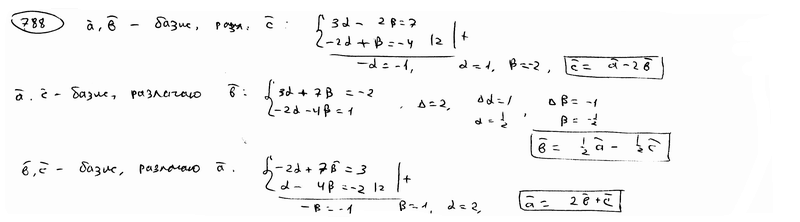 | | 789 | | Даны три вектора  ={3; -1}, ={3; -1}, 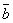 ={1; -2}, ={1; -2}, 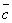 ={-1; 7}. Определить разложение вектора ={-1; 7}. Определить разложение вектора  по базису по базису  , ,  . .  | | 790 | | Принимая в качестве базиса векторы  и и  , совпадающие со сторонами треугольника АВС, опреедлить разложение векторов, приложенных в вершинах треугольника и совпадающие с его медианами. , совпадающие со сторонами треугольника АВС, опреедлить разложение векторов, приложенных в вершинах треугольника и совпадающие с его медианами. 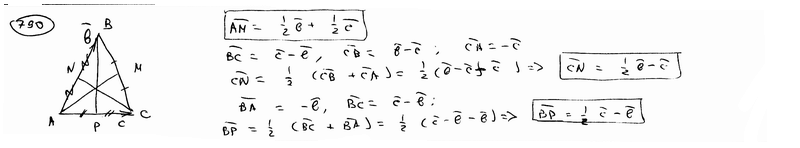 | | 791 | | На плоскости даны етыре точки A(1; -2), B(2; 1), C(3; 2), D(-2; 3). Определить разложение векторов 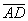 , , 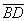 , , 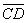 и и 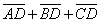 , принимая в качестве базиса векторы , принимая в качестве базиса векторы 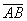 и и 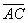 . . 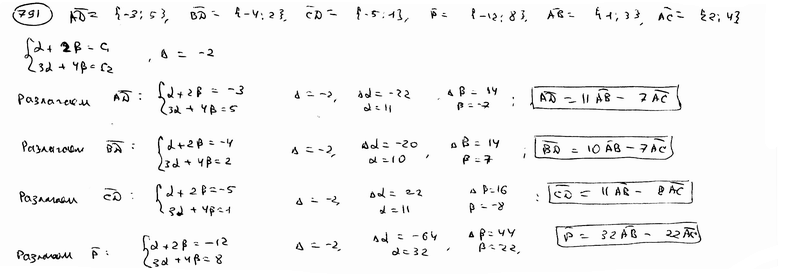 | | 792 | | Доказать, что если  , ,  , ,  - какие угодно некомпланарные векторы, то всякий вектор - какие угодно некомпланарные векторы, то всякий вектор  пространства может быть представлен в виде пространства может быть представлен в виде  . Доказать, что числа . Доказать, что числа 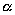 , , 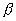 , , 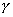 однознчно определяются векторами однознчно определяются векторами  , , 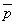 , ,  , ,  . (Представление вектора . (Представление вектора  в виде в виде  называется разложением его по базису называется разложением его по базису  , ,  , ,  . Числа . Числа  , ,  , ,  называются коэффициентами этого разложения. называются коэффициентами этого разложения.  | | 793 | | Даны три вектора  ={3; -2; 1}, ={3; -2; 1},  ={-1; 1; -2}, ={-1; 1; -2}, 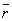 ={2; 1; -3}. Найти разложение вектора ={2; 1; -3}. Найти разложение вектора 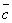 ={11; -6; 5} по базису ={11; -6; 5} по базису 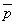 , , 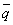 , ,  . .  | | 794 | | Даны четыре вектора  ={2; 1; 0}, ={2; 1; 0},  ={1; -2; 2}, ={1; -2; 2},  ={2; 2; -1}, ={2; 2; -1}, 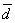 ={3; 7; -7}. Определить разложение каждого из этих четырех векторов, принимая в качестве базиса три остальных. ={3; 7; -7}. Определить разложение каждого из этих четырех векторов, принимая в качестве базиса три остальных.  | |
 ={6; 3; -2}.
={6; 3; -2}. 
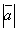 =13.
=13. 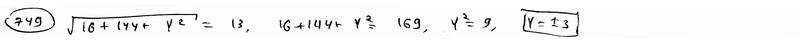
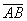 и
и 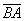 .
. 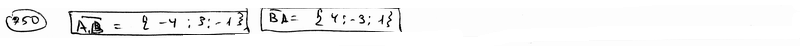
 ={3; -1; 4}, если его начало совпадает с точкой М(1; 2; -3).
={3; -1; 4}, если его начало совпадает с точкой М(1; 2; -3). 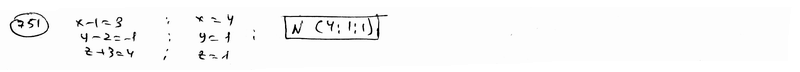
 ={2; -3; -1}, если его конец совпадает с точкой (1; -1; 2).
={2; -3; -1}, если его конец совпадает с точкой (1; -1; 2). 
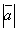 =2 и углы
=2 и углы 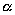 =450,
=450, 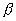 =600,
=600, 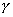 =1200. Вычислить проекции вектора
=1200. Вычислить проекции вектора  на координатные оси.
на координатные оси. 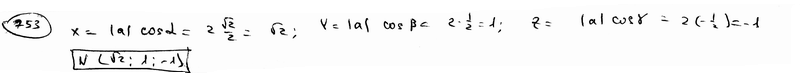
 ={12; -15; -16}.
={12; -15; -16}. 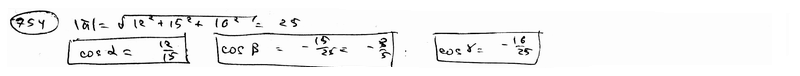
 ={3/13; 4/13; 12/13}.
={3/13; 4/13; 12/13}. 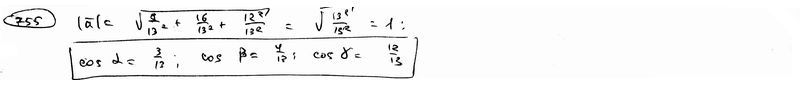
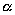 =450,
=450, 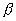 =600,
=600, 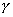 =1200;
=1200; 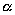 =450,
=450, 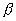 =1350,
=1350, 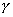 =600;
=600; 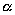 =900,
=900, 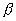 =1500,
=1500, 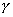 =600.
=600. 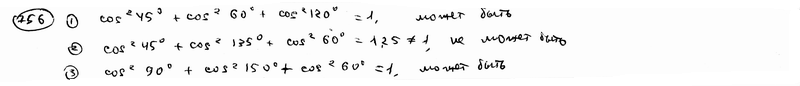
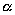 =300,
=300, 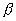 =450;
=450; 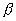 =600,
=600, 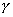 =600:
=600: 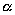 =1500,
=1500, 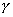 =300.
=300. 
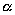 =1200 и
=1200 и 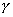 =450. Какой угол он составляет с осью Oy?
=450. Какой угол он составляет с осью Oy? 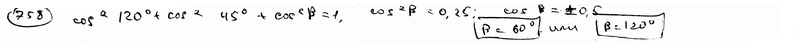
 составляет с координатными осями Ox и Oy углы
составляет с координатными осями Ox и Oy углы 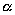 =600,
=600, 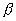 =1200. Вычислить его координаты при условии, что
=1200. Вычислить его координаты при условии, что 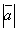 =2.
=2. 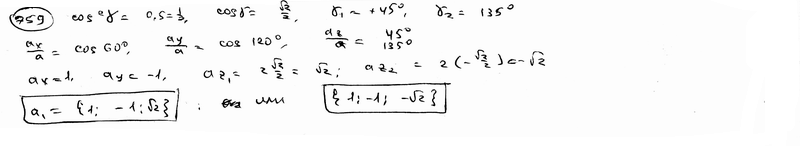
 Глава 30. Линейные операции над векторами
Глава 30. Линейные операции над векторами 
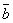 построить каждый из следующих векторов: 1).
построить каждый из следующих векторов: 1). 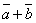 , 2).
, 2). 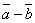 , 3).
, 3). 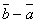 , 4).
, 4). 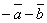 .
. 
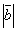 =19 и
=19 и 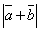 =24. Вычислить
=24. Вычислить 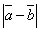 .
. 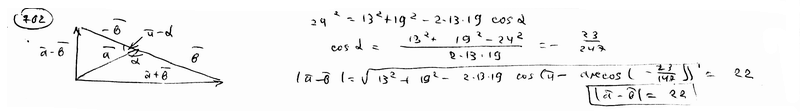
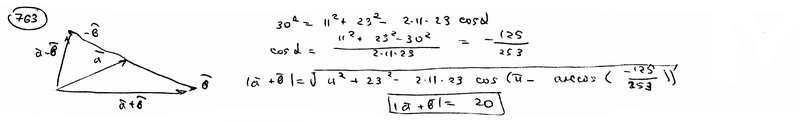
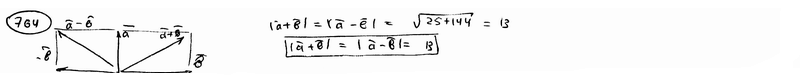
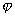 =600, причем
=600, причем 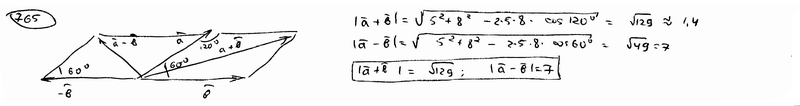
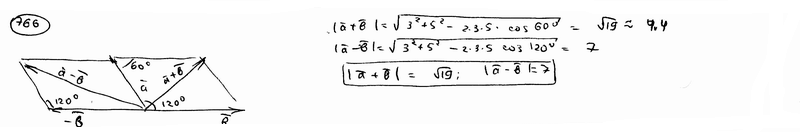
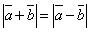 ;
; 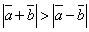 ;
; 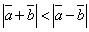 .
. 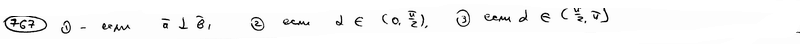

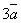 ;
; 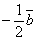 ;
; 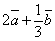 ;
; 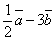 .
. 
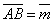 и вектор
и вектор 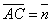 . Построить каждый из следующих векторов. Принимая в качестве масштабной единицы
. Построить каждый из следующих векторов. Принимая в качестве масштабной единицы 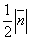 , построить также векторы:
, построить также векторы: 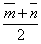 ;
; 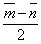 ;
; 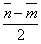 ;
; 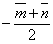 ;
; 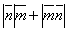 ;
; 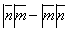 .
. 
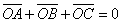 .
. 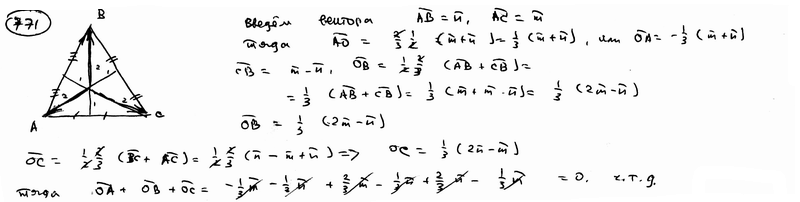
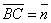 ,
, 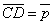 ,
, 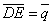 ,
, 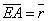 . Построить векторы:
. Построить векторы: 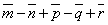 ;
; 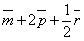 ;
; 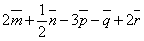 .
. 
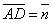 ,
, 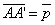 . Построить каждый из следующих векторов:
. Построить каждый из следующих векторов: 
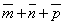 ;
; 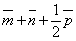 ;
; 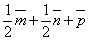 ;
; 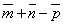 ;
; 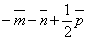 .
. 
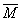 ,
, 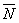 ,
, 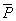 , приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину их равнодействующей
, приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину их равнодействующей 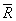 , если известно, что
, если известно, что 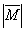 =2Н,
=2Н,  =10Н,
=10Н, 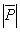 =11Н.
=11Н. 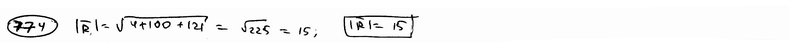
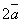 ;
; 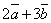 ;
; 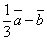 .
. 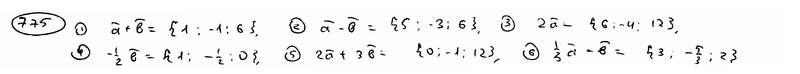
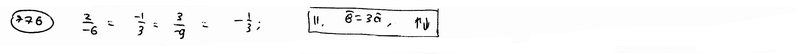
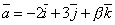 и
и 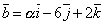 коллинеарны.
коллинеарны. 
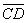 коллинеарны, установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны.
коллинеарны, установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны. 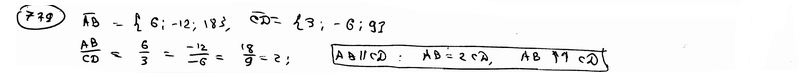

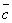 по базису
по базису 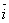 ,
, 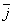 ,
, 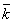 :
: 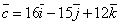 . Определить разложение по этому же базису вектора
. Определить разложение по этому же базису вектора 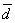 , параллельного вектору
, параллельного вектору 
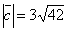 .
. 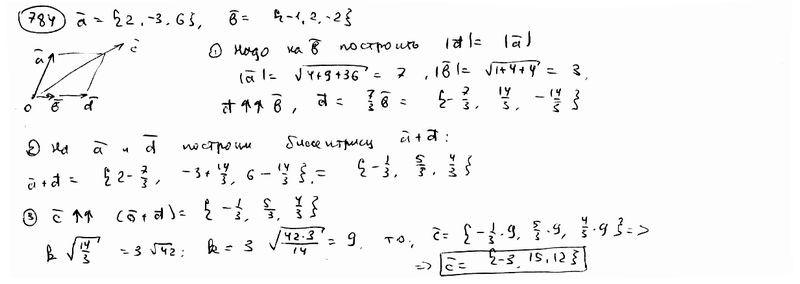
 ={4; 2; -2} совпадают со сторонами теругольника АВС. Определить координаты векторов, приложенных к вершинам треугольника и совпадающими с его медианами AM, BN, CP.
={4; 2; -2} совпадают со сторонами теругольника АВС. Определить координаты векторов, приложенных к вершинам треугольника и совпадающими с его медианами AM, BN, CP. 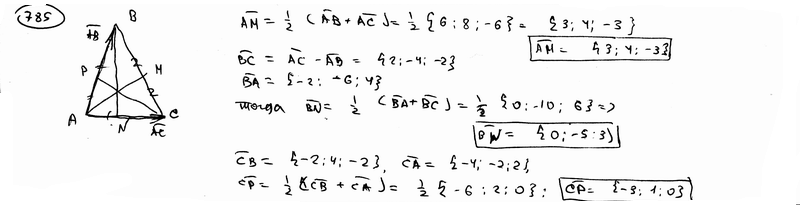
 и
и  - какие угодно неколлинеарные векторы, то всякий вектор, лежащих в их плоскости, может быть представлен в виде
- какие угодно неколлинеарные векторы, то всякий вектор, лежащих в их плоскости, может быть представлен в виде 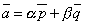 . Доказать, что числа
. Доказать, что числа 
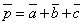 по базису
по базису 
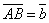 и
и 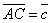 , совпадающие со сторонами треугольника АВС, опреедлить разложение векторов, приложенных в вершинах треугольника и совпадающие с его медианами.
, совпадающие со сторонами треугольника АВС, опреедлить разложение векторов, приложенных в вершинах треугольника и совпадающие с его медианами. 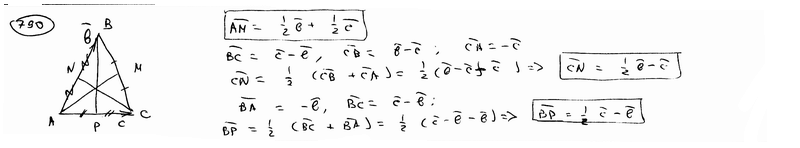
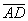 ,
, 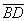 ,
, 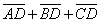 , принимая в качестве базиса векторы
, принимая в качестве базиса векторы 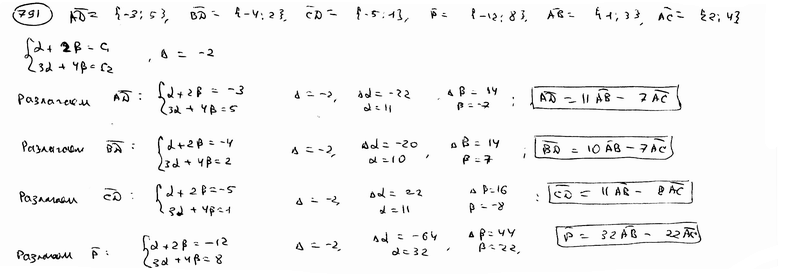
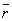 - какие угодно некомпланарные векторы, то всякий вектор
- какие угодно некомпланарные векторы, то всякий вектор 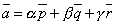 . Доказать, что числа
. Доказать, что числа