Записать формулы вычисления площадей поверхностей вращения с помощью определенного интеграла

Найдем площадь поверхности, которая образуется вращением кривой 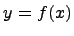вокруг оси 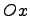, где .

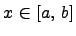Указанную площадь можно получить вычислением определенного интеграла:

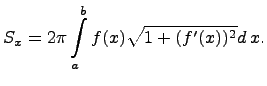
Теперь рассмотрим случай, когда вращаем кривую 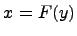вокруг оси 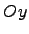, где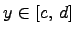

В этом случае площадь определяется вычислением следующего определенного интеграла:

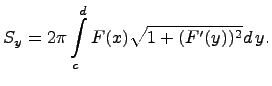
Записать формулу вычисления производной по направлению.

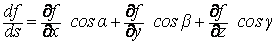
Записать формулу градиента функции

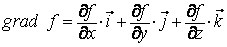
Записать уравнение касательной плоскости к поверхности

Записать уравнение нормали к поверхности

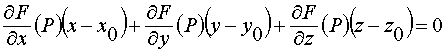
Привести метод вычисления двойных интегралов в декартовой системе координат

Пусть f(x, y) – непрерывная в замкнутой области D плоскости ОХУ функция. Если область D является правильной в направлении оси OY, то

.

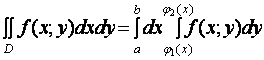Если область D является правильной в направлении оси OХ, то

.

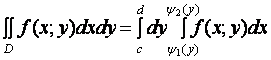Привести метод вычисления тройных интегралов в декартовой системе координат

Записать формулу тройного интеграла в цилиндрической системе координат

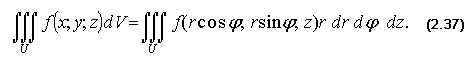
Записать формулу тройного интеграла в сферической системе координат

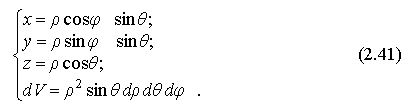
Привести метод вычисления криволинейных интегралов 1-го рода.

Привести метод вычисления криволинейных интегралов 2-го рода

Записать формулу Грина

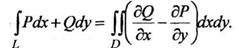
Записать формулу Остроградского

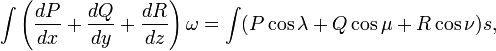
Записать формулу Стокса

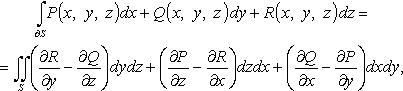
Записать вид Гамма-функции

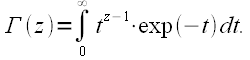
Записать вид Бета-функции

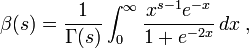
Как вычисляется дивергенция векторного поля?

Дивергенцией векторного поля 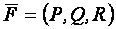называется скалярное поле, определяемое равенством

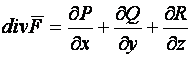
Как проверить, будет ли векторное поле соленоидальным?

Как вычисляется ротор векторного поля?

Ротором векторного поля 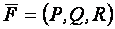называется векторное поле, определяемое вектором

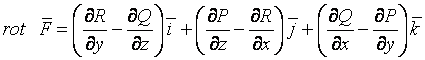
Сформулировать необходимое условие сходимости числового ряда.

Пусть числовой ряд u₁+u₂+...+u_n+... , сходится, а S - его сумма. Тогда при неограниченном возрастании числа n членов ряда его общий член u_n стремится к нулю.

Когда сходится/расходится обобщенный гармонический ряд?

Обобщенным гармоническим рядом называют ряд

.

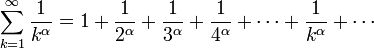Обобщенный гармонический ряд расходится при α≤1 и сходится при α>1

Сформулировать признаки сравнения числового ряда. Когда они применяются?

Если заданы ряды 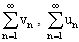и существует 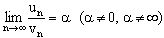, то ряды 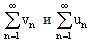сходятся либо расходятся одновременно.

Сформулировать признак Даламбера сходимости знакоположительных рядов. Когда он применяется?

Если существует 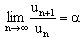то:
при 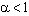ряд 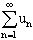сходится;
при 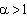ряд 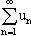расходится.

Сформулировать признак Коши сходимости знакоположительных рядов. Когда он применяется?

Дан ряд 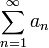, 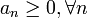. Пусть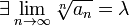

тогда:

1. Если 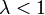ряд сходится;

2. Если 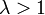ряд расходится.