Дифференциальные уравнения первого порядка с разделяющими переменными
1, Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х, искомую функцию у и ее производные или дифференциалы.
Символически дифференциальное уравнение записывается так:
, 
, 
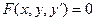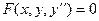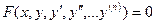
2. Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.
3. Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение.
4. Решением (или интегралом) дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.
5. Общим решением (или общим интегралом) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнений. Так, общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную.
6. Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находятся при определенных начальных значениях аргумента и функции.
7. Нахождение частного решения дифференциального уравнения по известным начальным данным из общего решения, называют задачей Коши.
8. График частного решения дифференциального уравнения называется интегральной кривой.
Общему решению дифференциального уравнения соответствует совокупность (семейство) всех интегральных кривых.
Дифференциальным уравнением первого порядка называется уравнение, в которое входят производные (или дифференциалы) не выше первого порядка.
Дифференциальное уравнение с разделяющимися переменными называется уравнение вида: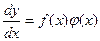 
.
Для решения этого уравнения нужно сначала разделить переменные: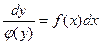 
, а затем проинтегрировать обе части полученного равенства:
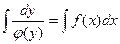
1. Найти общее решение уравнения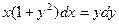 
.
Разделив переменные, имеем:
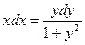
Интегрируем обе части полученного уравнения:
; 
.
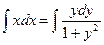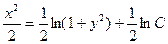Так как произвольная постоянная С может принимать любые числовые значения, то для удобства дальнейших преобразований вместо С мы написали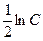 
. Потенцируя последнее равенство, получим: 
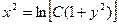. Это и есть общее решение данного уравнения.
2. Найти общее решение уравнения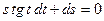 
, удовлетворяющее начальным условиям 
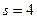при 
.
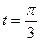Разделив переменные, имеем:
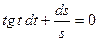
Проинтегрируем обе части полученного уравнения:
, 
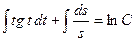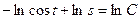, или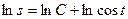 
, 
.
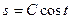Это общее решение данного уравнения. Для нахождения значения произвольной постоянной С подставим значение 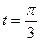и 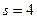в выражение для общего решения: 
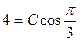, или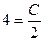 
, откуда С = 8.
Следовательно, искомое частное решение, удовлетворяющее указанным начальным условиям имеет вид: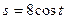 
.