Второй замечательный предел

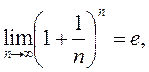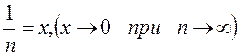если то 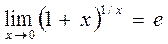в частности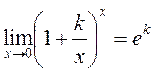

4. При нахождении пределов вида 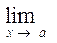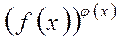=С, нужно иметь в виду следующее:

1) если существуют конечные пределы

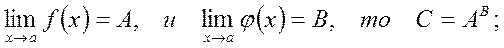
2) если 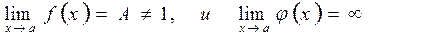то предел находится с помощью формул:

а) если 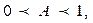то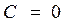

б) если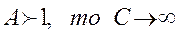

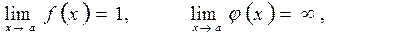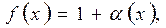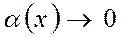3) если то полагают где при 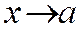и следовательно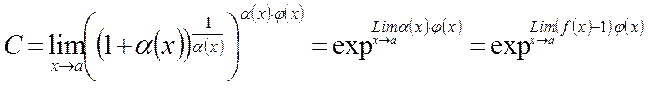

Чтобы раскрыть неопределенность вида , заданную отношением двух многочленов, надо в числителе и в знаменателе выделить критический множитель (т.е. множитель, равный нулю при предельном значении х) и сократить на него.

Пример.Найти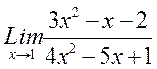

Решение.При х = 1 числитель и знаменатель обращаются в нуль, получается неопределенность вида 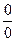. Преобразуем данную функцию, разлагая на множители числитель и знаменатель по формул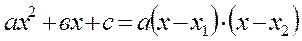е где 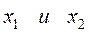- корни уравнения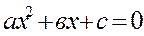

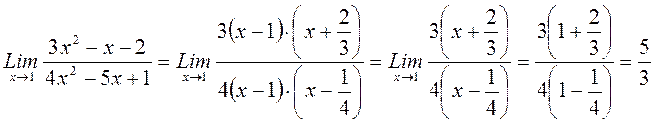6. Чтобы раскрыть неопределенность вида 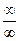, заданную отношением двух многочленов, надо числитель и знаменатель разделить на самую высокую входящую в них степень х, а затем перейти к пределу.

Пример. Найти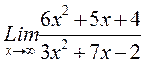

Решение. При 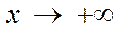числитель и знаменатель неограниченно увеличиваются (получаем неопределенность вида 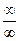). Разделим числитель и знаменатель на 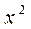, т.е. на старшую степень х. Получим:

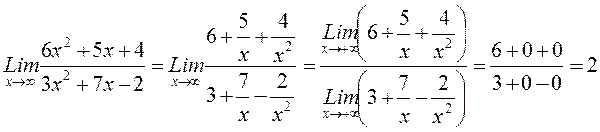
Здесь принято во внимание, что , , .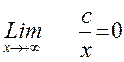

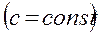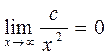Чтобы раскрыть неопределенность вида , в которой числитель и знаменатель содержат иррациональность, следует соответствующим образом избавится от иррациональности.

Пример.Найти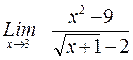

Решение При х = 3 числитель и знаменатель дроби обращаются в нуль. Избавимся от иррациональности в знаменателе, умножая числитель и знаменатель на .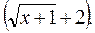

=

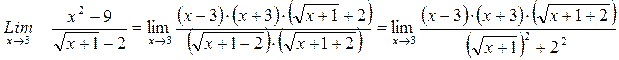
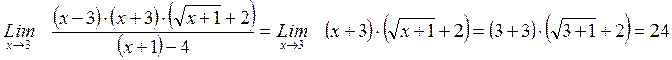
Пример. Найти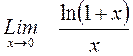

Решение Так как 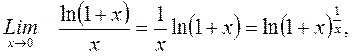то

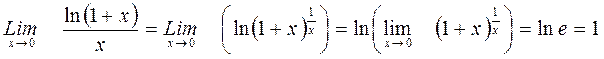
Пример. Найти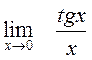

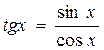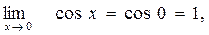Решение. Так как и то

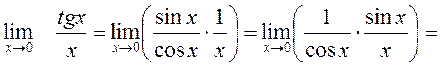
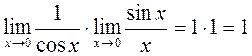
Пример. Найти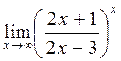

Решение. Это предел вида 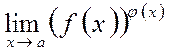, где 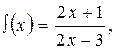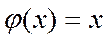На основании формул 4 имеем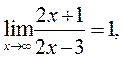 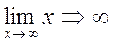, т.е. предел вида 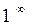; в соответствии с третьим случаем из формул 4 имеем

℮ = ℮ = ℮ =

℮ = ℮ = ℮

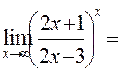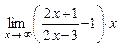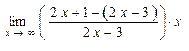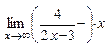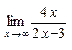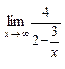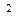
4.2. Производная и дифференциал. Основные определения и свойства.

Производной функции в точке называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т.е.

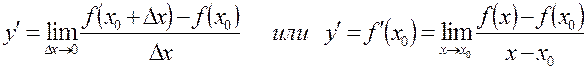
Основные правила дифференцирования

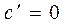
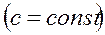
Если 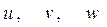- дифференцируемые функции от х, то

.

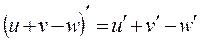
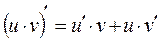
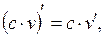
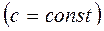
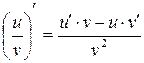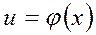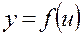Если , а , то 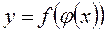имеет производную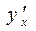 , т.е.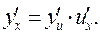

Производные основных элементарных функций

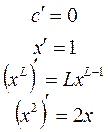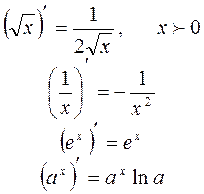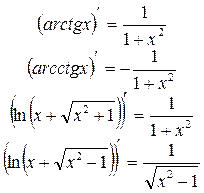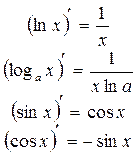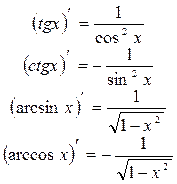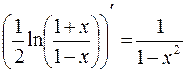Пример. Найти производные функций

а)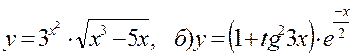

Решение. а)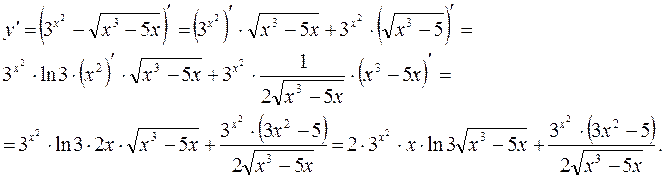

б)

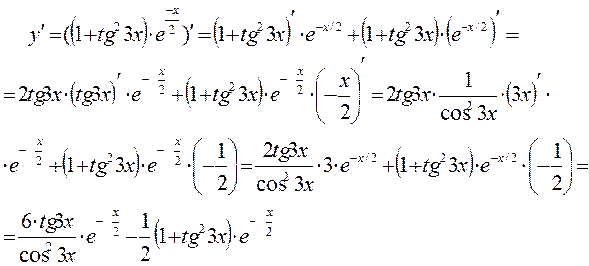
Дифференциалом функции 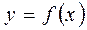называется произведение ее производных на приращение независимой переменной: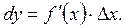

В частности, при 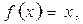получим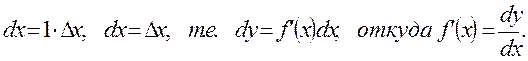

Применение дифференциала к приближенным вычислениям

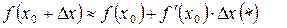
Пример. Вычислить приблизительно значение функци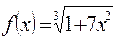и: при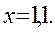

Решение. Введем 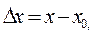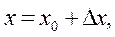в нашем случае 1,1 = 1+0,1 или

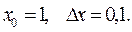
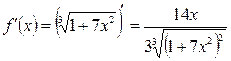
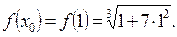
Воспользуемся формулой (*)

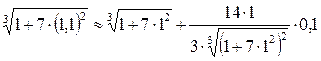
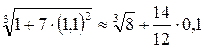
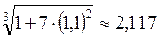
Пример. Вычислить приближенно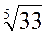

Решение. 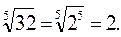Введем 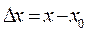, т.е. 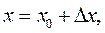найдем приближенно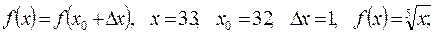

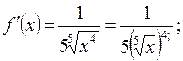тогда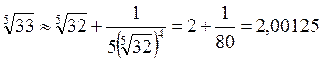

4.3. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ

Правило Лопиталя-Бернулли

(раскрытие неопределенностей вида )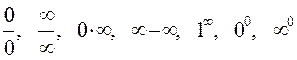

Пусть функции 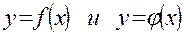дифференцируемы, причем производная одной из них не обращается в нуль.

Если 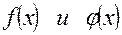- обе бесконечно малые или обе бесконечно большие при 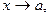т.е. если частное 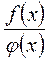представляет в точке 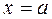неопределенность типа 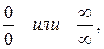то 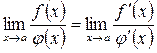при условии, что предел отношения производных существует.

1. Для раскрытия неопределенностей типа 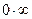, необходимо преобразовать существующее произведени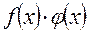е , где

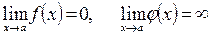, частности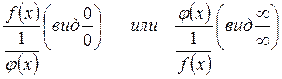

2. В случае неопределенности вида 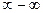, преобразуем разность

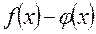, где 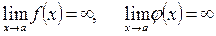, в произведение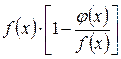

И раскрыть сначала неопределенность 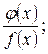если 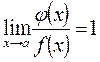, то следует привести выражение к виду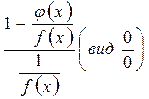

3. Неопределенность видов 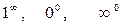раскрывается с помощью предварительного логарифмирования и нахождения предела степени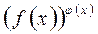

Пример. Найти

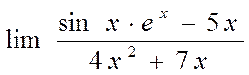
Решение. При 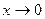получаем неопределенность вида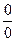

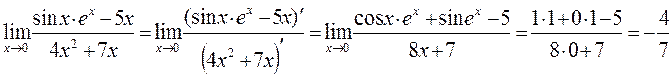
Пример. Найти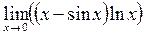

Решение. При 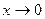имеем неопределенность 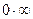. Данную функцию можно представить в виде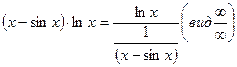

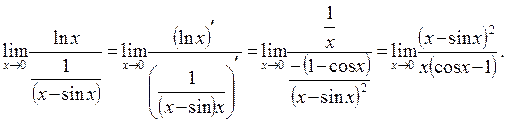
Это – неопределенность вида 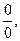поэтому 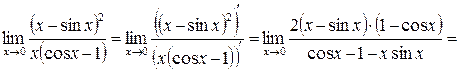(еще раз применим правило Лопитоля) =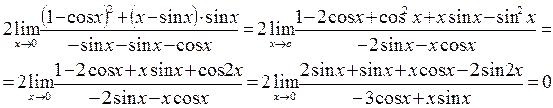

Итак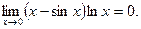

§ Касательная и нормаль к кривой

Уравнение касательной к кривой 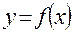в точке 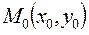имеет вид:

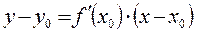
Уравнение нормали к кривой 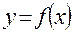в точке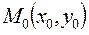

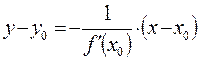
Пример. Составить уравнения касательной и нормали к линии 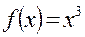в точке .

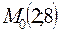Решение. Находим производную данной функции и ее значение при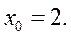

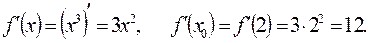
Подставляя значения 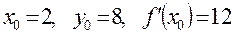в уравнения касательной и нормали получим: 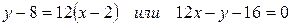- уравнение касательной

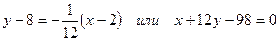уравнение нормали.

§ Применение производной в экономике. Эластичность функции.

Пусть одна функция 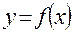, для которой существует производная 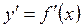. Эластичностью функции 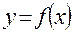относительно переменной х называют предел 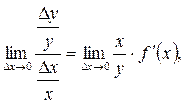его обозначают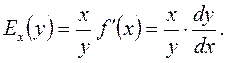

Эластичность относительно х есть приближенный процентный прирост функции (повышение или понижение), соответствующий приращению независимой переменной на 1%.

Пример. Рассчитать эластичность функции 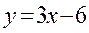и найти значение показателя эластичности при х=10.

Решение. Находим: 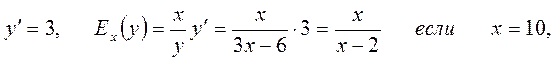то

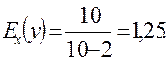Это означает, что если х возрастает на 1%, то у увеличится на 1,25%.

Пример. Найти эластичность предложения s, т.е. количество товара, предлагаемого на продажу в единицу времени, если предложение зависит от цены p, так как s=s (p).

Решение. Величина 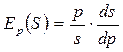показывает, как изменится предложение с увеличением цены на 1%.

Пусть 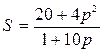- функция предложения (установлена опытным путем),

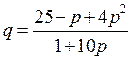- функция спроса.

Определим цену равновесия, т.е. цену, при которой спрос и предложение уравновешиваются, эластичность спроса и предложения для этой цены.

Найдем цену равновесия из условия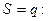

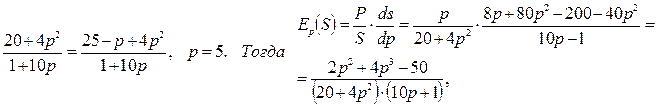
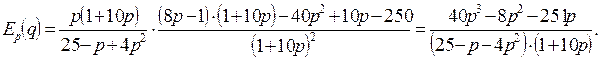
При р=5 имеем: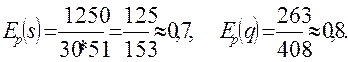

Т.о., при цене р=5 эластичность спроса 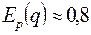. Предположим, что требуется повысить цену на товар на 10%, что вызовет снижение спроса на данный товар на 8%. Доход при этом повысится на 2%. Если же цену увеличить на 50%, то спрос уменьшится на 40%, доход увеличится на 10%.

§ Исследование функций и построение графиков

Схема.

1) Указать область определения функции;

2) найти точки разрыва функции, точки пересечения ее графика с осями координат и вертикальные асимптоты (если они существуют);

3) определить четность (нечетность), периодичность функции;

4) исследовать функцию на монотонность и экстремум;

5) определить интервалы выпуклости (вогнутости) и точки перегиба;

6) найти асимптоты графика функции;

7) произвести необходимые дополнительные вычисления;

8) построить график функции.

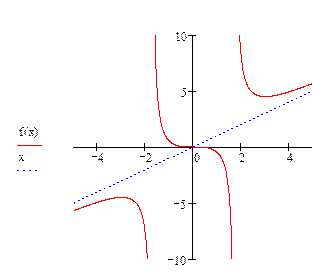
Пример. Исследовать функцию 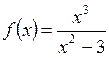и построить ее график

Решение. 1). ОДЗ: 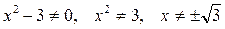т.е.

хє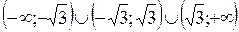

2).

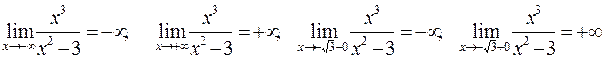
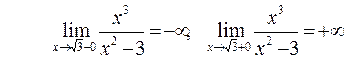
т.о. 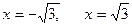, точки разрыва функции и вертикальные асимптоты

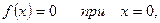т.е. 0 (0; 0) точка пересечения с осями координат.

3. 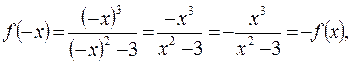т.е. функция нечетная, значит график симметричен относительно начала координат.

4). Находим точки экстремума функции

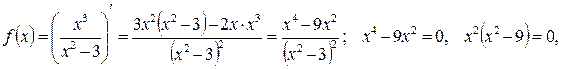
откуда 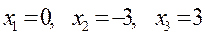исследуем знак второй производной при этих значениях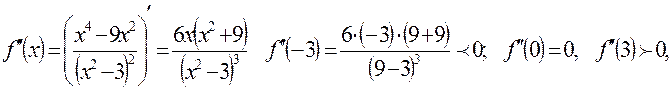

т.о. х=-3 – точка max, х=3 – точка min т.к. 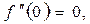то по правилу нахождения экстремума 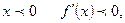при при 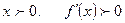знак не меняется, значит х=0 не является точкой экстремума.

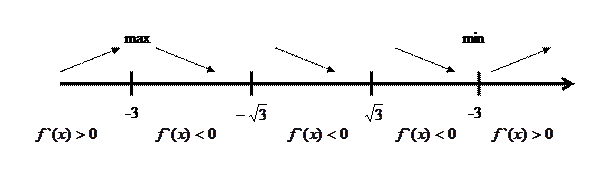
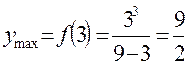
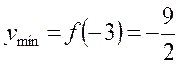
5). Определим интервалы выпуклости (вогнутости) и точки перегиба.

,

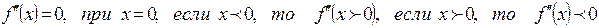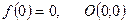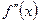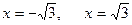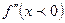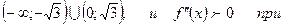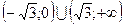значит х=0 является точкой перегиба, т.е. Т.к. не определена в точках что и сама функция и когда хє хє , то

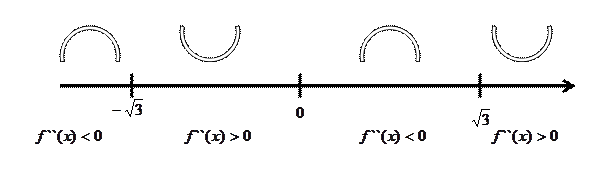
6). Находим наклонные асимптоты графика функции.

Если существуют пределы 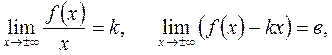то прямая 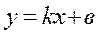является наклонной асимптотой графика функции. Т.е. в нашем случае

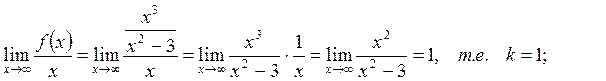
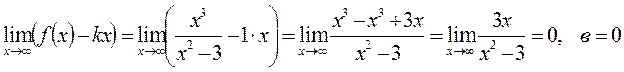
Получаем, что у =х – наклонная асимптота.

7).

х		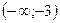-3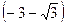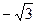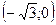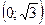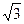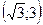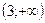
у	-	-	-	±	+		-	±	+	+	+
	+		-	±	-		-	±	-		-
	-	-	-	±	+		-	±	+	+	+
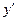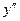выводы	↗	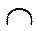	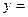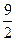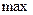↘	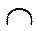асимптота	↘	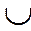точка перегиб	↘	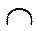асимптота	↘		↗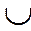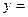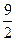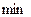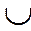

8).

§ Задачи на экстремум

Пример. Из квадратного листа жести со стороной 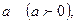вырезая по углам равные квадраты и сгибая края, составляют прямоугольную коробку. Найти наибольшую вместимость коробки.

Решение. Если сторону вырезанного квадрата принять за х, то объем коробки 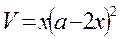, где хє 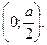Теперь надо найти наибольшее значение функции V на этом промежутке. Критические точки получим из условия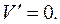

Имеем:

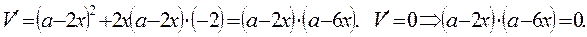
Так как 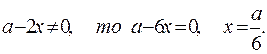Находим:

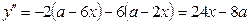
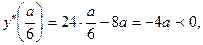следовательно, при 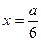функция V имеет максимум, но это и будет наибольшее значение. Итак, наибольшая вместимость коробки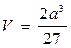

Пример. Консервная банка имеет форму цилиндра. Каковы должны быть ее размеры, чтобы при заданном объеме V на ее изготовление пошло наименьшее количество материала?

Решение. Наименьшее количество материала будет израсходовано при наименьшей полной поверхности банки. Пусть h – высота банки, х – радиус ее основания. Тогда: 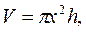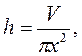хє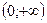

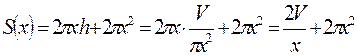
Найдем:

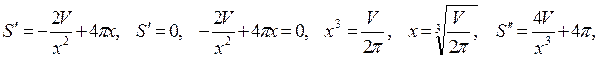
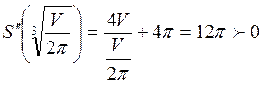
Следовательно, функция S(x) имеет минимум при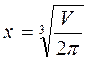

Найдем высоту: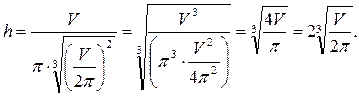

Таким образом, высота равна диаметру основания.

Пример. Некоторое предприятие стремиться к максимальной прибыли. Оно может либо увеличить объем производства, не изменяя цены, либо не изменять объема, а увеличить цену соответственно спросу. Какой путь наиболее экономически выгодный?

Решение. Пусть предприятие производит х единиц продукции по цене р(х), тогда выручка 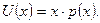Прибыль 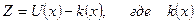- издержки производства. Прибыль максимальна, если 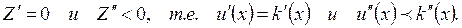Таким образом, предельная выручка равна предельным издержкам и темп роста предельной выручки меньше темпа роста предельных издержек.

Пусть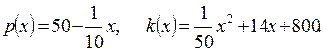

Тогда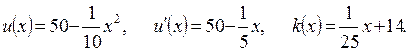

Следовательно,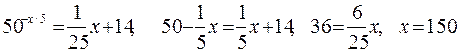

Оптимальный объем производства 150 единиц. В этом случае цена

р=50-15=35. Выручка 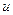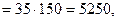издержки производства.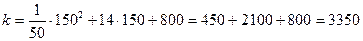

Прибыль Z=5250-3350=1900.

Вопросы к зачету

По дисциплине «Высшая математика»

1.Определение скаляра и вектора. Равенство векторов. Модуль вектора, коллинеарные, компланарные, связные, свободные, единичные векторы.

2.Линейные операции над векторами. Сложение, вычитание, умножение вектора на скаляр в векторной и координатной формах.

3.Проекция вектора на ось. Скалярное произведение векторов в векторной и координатной формах.

4.Угол между векторами, условие перпендикулярности двух векторов в векторной и координатной формах.

5.Прямая на плоскости. Общее и векторное уравнение прямой на плоскости.

6.Уравнение прямой с угловым коэффициентом. Уравнение прямой, проходящей через две данные точки.

7.Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых. Нормальное уравнение прямой. Расстояние от точки до прямой.

8.Плоскость в пространстве. Общее и векторное уравнения плоскости. Условие параллельности и перпендикулярности плоскостей.

9.Нормальное уравнение плоскости. Расстояние от точки до плоскости. Уравнение плоскости в отрезках.

10.Параметрические и канонические уравнения прямой в пространстве. Угол между двумя прямыми, условие параллельности и перпендикулярности двух прямых в пространстве.

11.Угол между прямой и плоскостью. Условие параллельности и перпендикулярности прямой и плоскости. Точка пересечения прямой и плоскости.

12.Понятие линейного вектора пространства. Линейно зависимые и линейно независимые вектора. Базис и размерность линейного пространства. Разложение вектора в базисе. Линейное преобразование координат при изменении базиса.

13.Понятие матрицы и ее типы. Равенство матриц. Размерность матрицы. Определение ранга матриц.

14.Линейные операции над матрицами. Умножение матриц. Условие согласованности матриц. Транспонирование матриц.

15.Понятие определителя матрицы. Равенство определителей. Основные свойства определителей.

16.Определители 2-го и 3-го порядков и их вычисление. Разложение определителей по элементам строки или столбца. Алгебраические дополнения и миноры. Понятие определителя n-го порядка.

17.Обратная матрица, условия ее существования и построение.

18.Системы линейных алгебраических уравнений (СЛАУ) и их решение. Условия совместности и несовместности, определенности и неопределенности для линейных систем.

19.Однородные и неоднородные СЛАУ. Теорема и формулы Крамера для решения линейных систем с помощью определителей.

20.Решение СЛАУ с помощью метода Гаусса. Правило прямоугольника. Теорема Кронекера-Капелли.

21.Итерационные методы решения линейных систем.

22.Постоянные и переменные величины. Понятие функции и функциональной зависимости. Область определения и способы задания функции.

23.Основные элементы функции. Понятие сложной и обратной функции.

24.Понятие предела последовательности. Предел и непрерывность функции. Точки разрыва функции.

25.Нахождение пределов функций. Раскрытие неопределенностей с помощью правила Лопиталя-Бернулли. Замечательные пределы.

26.Производная функции в точке, ее определение, геометрическая, физическая и экономическая интерпретация.

27.Основные правила дифференцирования. Производная сложной и обратной функций.

28.Производные основных элементарных функций. Таблица производных

29.Исследование функций и построение графиков.

30.Приложения дифференциала.

Литература:

1.Высшая математика. Общий курс, под ред. Яблонского А.И. Мн.: Выш. школа, 1993.

2.Сборник задач по общему курсу высшей математики. Под ред. Яблонского А.И. Мн.: Выш. школа, 1994.

3.Сборник задач и упражнений по высшей математике. Теория вероятностей и математическая статистика. Мн.: Выш. школа, 1996.

4.Лихолетов И.И. Высшая математика, теория вероятностей и математическая статистика. Мн.: Выш. школа, 1976.