Свойства неопределенных интегралов
ПЛАН
1. Первообразная функция и неопределенный интеграл.
2. Свойства неопределенных интегралов.
3. Таблица основных неопределенных интегралов.
Первообразная функция и неопределенный интеграл
Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции.
Интегральное исчисление решает обратную задачу – нахождение самой функции по ее производной или дифференциалу.
Определение. Функция F(x) называется первообразнойдля функции f(х) на
промежутке Х, если в каждой точке х этого промежутка выпол-
няется равенство  .
.
В простейших случаях первообразную можно найти сразу, зная формулы для производных. Например, очевидно, что если 
 Если функция f(х) имеет первообразную, то она имеет их бесчисленное множество. Например, функции
Если функция f(х) имеет первообразную, то она имеет их бесчисленное множество. Например, функции  соответствует множество первообразных:
соответствует множество первообразных: 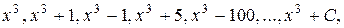 т.к.
т.к.  ,
, 
Таким образом, справедлива лемма о первообразных: если функция F(х) – первообразная для функции f(х) на промежутке Х, то функция F(x) + C, где С – const, является первообразной для функции f(х) на том же промежутке  . Однако, более глубоким является такой вопрос: существует ли у функции f(х) первообразные другого вида, чем F(х) + С. Оказывается не существует. Справедлива следующая теорема.
. Однако, более глубоким является такой вопрос: существует ли у функции f(х) первообразные другого вида, чем F(х) + С. Оказывается не существует. Справедлива следующая теорема.
Теорема. Если F(x) и Ф(х) – две любые первообразные функции для f(х), то
они могут различаться лишь на постоянное слагаемое, т.е.
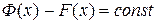 .
.
Доказательство. Так как F(x) и Ф(х) первообразные для f(х), то  и
и 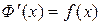 . Поэтому
. Поэтому  . А это означает, что
. А это означает, что  , где С – постоянное число. Следовательно,
, где С – постоянное число. Следовательно, 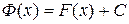 .
.
Определение. Совокупность всех первообразных для функции f(х) на проме- жутке Х называется неопределенным интегралом от функции f(х) на этом промежутке и обозначается  , где
, где  - знак
- знак
интеграла, f(х) - подынтегральная функция, f(x)d x – подынте-
гральное выражение.
Таким образом, 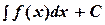 , (1)
, (1)
где  , С – произвольная постоянная.
, С – произвольная постоянная.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.

Назовем график первообразной от f(х) инте-
гральной кривой. Таким образом, если
 , то график функции у = F(x) есть
, то график функции у = F(x) есть
интегральная кривая. Неопределенный интеграл
геометрически представляет семейство всех ин-
тегральных кривых. Все кривые из этого семей-
Рисунок 1 ства у = F(x) + С могут быть получены из
одной интегральной кривой параллельным
сдвигом в направлении оси Оу.
Теорема. Всякая непрерывная на множестве Х функция f(х) имеет на этом
множестве первообразную, а следовательно, и неопределенный
интеграл.
Свойства неопределенных интегралов
1. Производная от неопределенного интеграла равна подынтегральной функции, т.е.  .
.
Доказательство. Дифференцируя левую и правую часть равенства (1), получаем:  .
.
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. 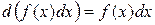 .
.
Доказательство. По определению дифференциала и свойству 1 имеем: 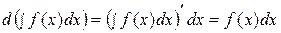 .
.
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.  .
.
Доказательство. По определению дифференциала и рассматривая функцию F(x) как первообразную для некоторой функции f(х) имеем 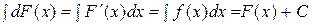 .
.
4. Постоянный множитель можно выносить за знак интеграла, т.е.  .
.
Доказательство. 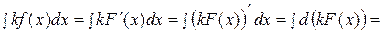
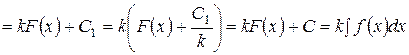 (положили
(положили 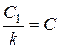 ).
).
5. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций, т.е. 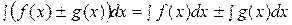 .
.
Доказательство. Пусть 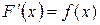 и
и  . Тогда
. Тогда 
 , где
, где  .
.
6. (Инвариантность формулы интегрирования). Если  , то и
, то и 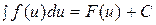 , где
, где  - произвольная функция, имеющая непрерывную производную.
- произвольная функция, имеющая непрерывную производную.
Доказательство. Пусть х - независимая переменная, f(х) – непрерывная функция и F(x) – ее первообразная. Тогда  . Положим
. Положим  , где
, где  - непрерывно-дифференцируемая функция. Рассмотрим сложную функцию
- непрерывно-дифференцируемая функция. Рассмотрим сложную функцию 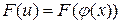 . В силу инвариантности формы дифференциала первого порядка функции имеем
. В силу инвариантности формы дифференциала первого порядка функции имеем  . Отсюда
. Отсюда  .
.
Таким образом, формула для неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой функцией от нее, имеющей непрерывную производную.
Таблица основных неопределенных интегралов
Интегралы в приводимой ниже таблице называются табличными.
В интегральном исчислении нет простых и универсальных правил отыскания первообразных от элементарных функций. Методы нахождения первообразных сводятся к указанию приемов, приводящих данный интеграл к табличному. Поэтому, необходимо знать табличные интегралы и уметь их узнавать.
В таблице основных интегралов переменная интегрирования U может обозначать как независимую переменную, так и функцию от независимой переменной (согласно свойству инвариантности формулы интегрирования).
Таблица интегралов
Формулы интегрирования
| Название интеграла | Простые функции | № | Сложные функции  | ||
| От дифференциала |  | 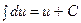 | |||
| От степенной функции |  |  | |||
| От показательной функции |  |  | |||
| От экспоненты |  |  | |||
| От синуса |  | 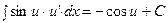 | |||
| От косинуса | 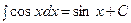 | 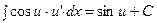 | |||
| От тангенса | 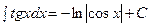 |  | |||
| От котангенса |  | 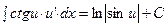 | |||
| Интеграл, дающий тангенс | 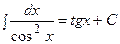 |  | |||
| Интеграл, дающий котангенс |  |  | |||
| Интеграл, дающий логарифм знаменателя |  |  | |||
| Интеграл, дающий арктангенс |  | 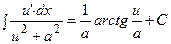 | |||
| Интеграл, дающий «высокий логарифм» |  |  | |||
| Интеграл, равный удвоенному знаменателю |  | 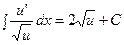 | |||
| Интеграл, дающий арксинус | 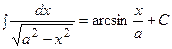 | 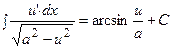 | |||
| Интеграл, дающий «длинный логарифм» |  |  | |||
Справедливость приведенных формул проверяется непосредственно дифференцированием.
Докажем, например, формулу (12).

 .
.
Получили подынтегральную функцию. Аналогично проверяется справедливость всех формул.
