Последовательность. Ограниченные последованности. Монотонные последовательности

Ограниченные и неограниченные последовательностиВ предположении о линейной упорядоченности множества 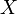элементов последовательности можно ввести понятия ограниченных и неограниченных последовательностей.

Ограниченная сверху последовательность — это последовательность элементов множества 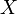, все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется верхней гранью данной последовательности.

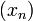ограниченная сверху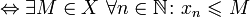

Ограниченная снизу последовательность — это последовательность элементов множества 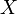, для которой в этом множестве найдётся элемент, не превышающий всех её членов. Этот элемент называется нижней гранью данной последовательности.

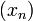ограниченная снизу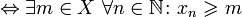

Ограниченная последовательность (ограниченная с обеих сторон последовательность) — это последовательность, ограниченная и сверху, и снизу.

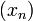ограниченная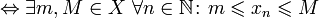

Неограниченная последовательность — это последовательность, которая не является ограниченной.

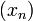неограниченная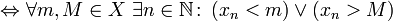

Монотонная последовательность — это невозрастающая, либо неубывающая последовательность. При этом предполагается, что на множестве, из которого берутся элементы последовательности, введено отношение порядка.

2. Бесконечно большие и бесконечно малые последовательности Бесконечно малая последовательность — это последовательность, предел которой равен нулю. Бесконечно большая последовательность — это последовательность, предел которой равен бесконечности. Свойства: Сумма двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

§ Разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

§ Алгебраическая сумма любого конечного числа бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

§ Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.

§ Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

§ Любая бесконечно малая последовательность ограничена.

§ Если стационарная последовательность является бесконечно малой, то все её элементы, начиная с некоторого, равны нулю.

§ Если вся бесконечно малая последовательность состоит из одинаковых элементов, то эти элементы — нули.

§ Если 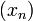— бесконечно большая последовательность, не содержащая нулевых членов, то существует последовательность 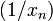, которая является бесконечно малой. Если же 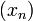всё же содержит нулевые элементы, то последовательность 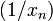всё равно может быть определена, начиная с некоторого номера 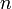, и всё равно будет бесконечно малой.

§ Если 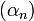— бесконечно малая последовательность, не содержащая нулевых членов, то существует последовательность 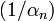, которая является бесконечно большой. Если же 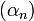всё же содержит нулевые элементы, то последовательность 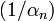всё равно может быть определена, начиная с некоторого номера 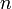, и всё равно будет бесконечно большой.

3. Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого.

4. Преде́л фу́нкции (предельное значение функции) в заданной точке,предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Свойства пределов функции 1) Предел постоянной величины.Предел постоянной величины равен самой постоянной величине:

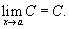
2) Предел суммы.Предел суммы двух функций равен сумме пределов этих функций:

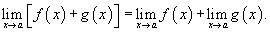
Аналогично предел разности двух функций равен разности пределов этих функций.Расширенное свойство предела суммы: Предел суммы нескольких функций равен сумме пределов этих функций:

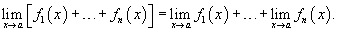
Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

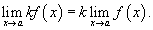
4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций: