Расчетно-графическая работа №7
«Определение главных центральных моментов инерции составных сечений, состоящих из стандартных профилей, имеющих ось симметрии»
Теоретическое обоснование.
Координаты центра тяжести сечения можно выразить через статический момент:
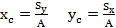
где относительно оси Оx 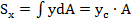
относительно оси Оy 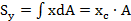
Статический момент площади фигуры относительно оси, лежащей в этой же плоскости, равен произведению площади фигуры на расстояние ее центра тяжести до этой оси. Статический момент имеет размерность 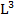 . Статический момент может быть величиной положительной, отрицательной и равен нулю (относительно любой центральной оси).
. Статический момент может быть величиной положительной, отрицательной и равен нулю (относительно любой центральной оси).
Осевым моментом инерции сечения называется взятая по всему сечению сумма произведений или интеграл элементарных площадок на квадраты их расстояний до некоторой оси, лежащей в плоскости рассматриваемого сечения
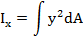
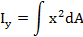
Осевой момент инерции выражается в единицах - 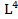 . Осевой момент инерции- величина всегда положительная и не равна нулю.
. Осевой момент инерции- величина всегда положительная и не равна нулю.
Оси, проходящие через центр тяжести фигуры, называются центральными. Момент инерции относительно центральной оси называется центральным моментом инерции.
Момент инерции относительно какой-либо оси равен центральному моменту инерции относительно оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями.
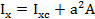

Из ряда параллельных осей момент инерции будет наименьшим относительно центральной оси.
Моменты инерции некоторых простых фигур:
для круга 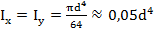
для кольца 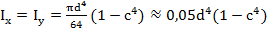
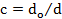
для полукруга 
для квадрата 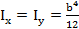
для прямоугольника 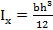
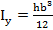
для треугольника 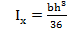
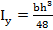
Размеры и геометрические характеристики профилей стандартного проката приведены в таблицах ГОСТа (см. Приложение).
Алгоритм решения
1. Определяют положение центра следователь тяжести сечения, а следовательно, и главных центральных осей (через статический момент)
2. Вычисляют (или берут) из таблиц значения моментов инерции отдельных частей сечения относительно собственных центральных осей, параллельных главным центральным осям всего сечения
3. Вычисляют моменты инерции частей, составляющих сечение, относительно его главных центральных осей. При этом используют зависимость между моментами инерции относительно параллельных осей
4. Определяют главные центральные моменты инерции всего сечения путем суммирования для каждой из главных осей
ЗАДАНИЕ
Вычислить главные центральные моменты инерции плоского сечения. Для решения своего варианта задачи использовать данные к РГР№5
Пример выполнения
Вычислить главные центральные моменты инерции плоского сечения.
ЗАДАЧА
Вычислить главные центральные моменты инерции плоского сечения.
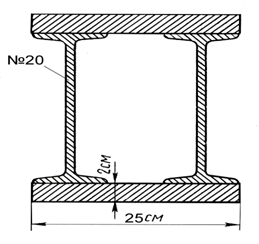
Решение
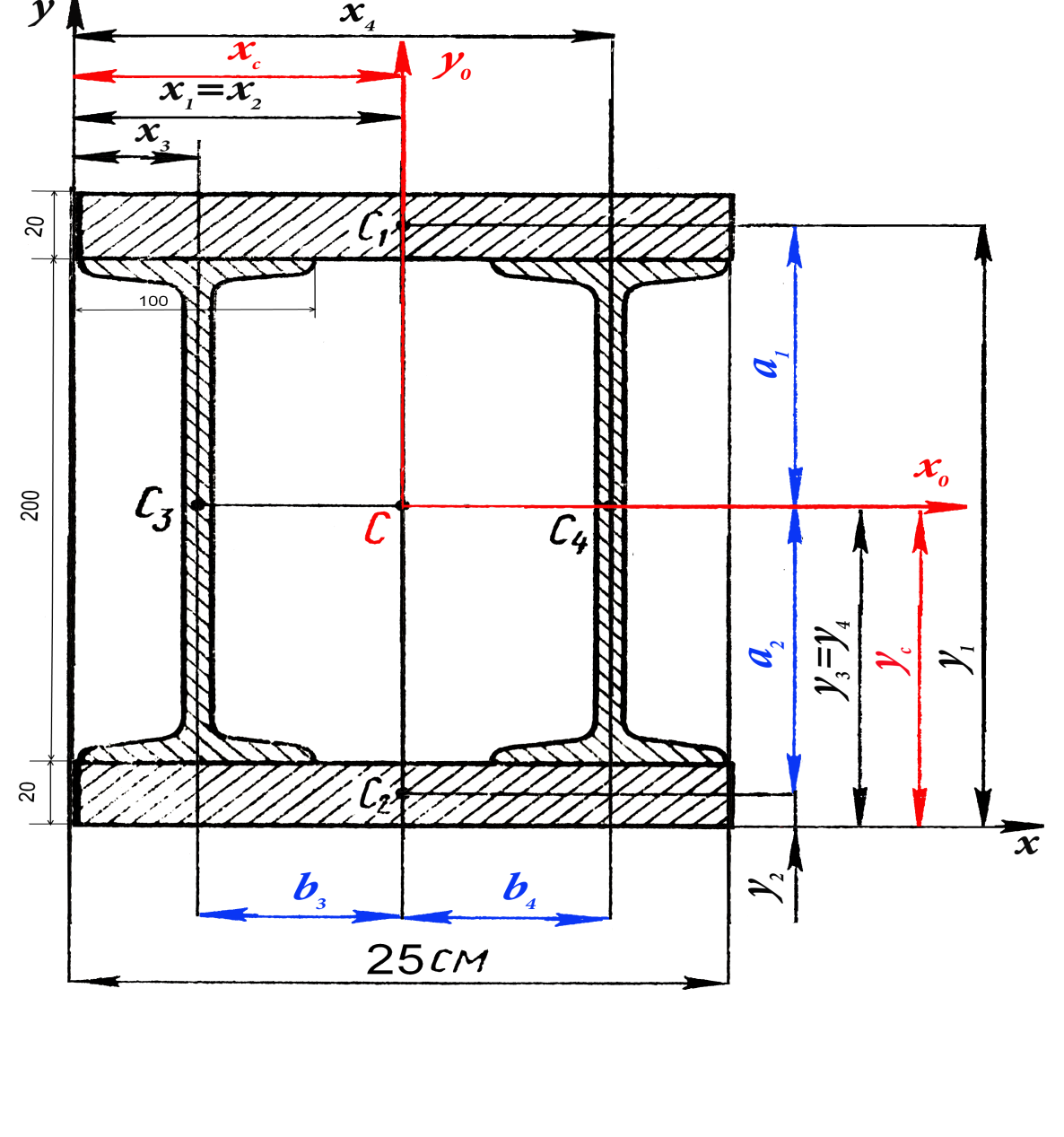
1. Чертим чертеж в масштабе 1:2
2. Проводим оси координат и отмечаем точку О
3. Разбиваем сложную фигуру на простые
I – прямоугольник
II - прямоугольник
III- двутавр
IV- двутавр
4. Вычислением и из таблиц (см. приложение) находим
- для прямоугольника 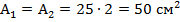
- для двутавра площадь 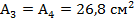
( 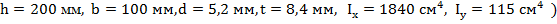
Площадь всей фигуры
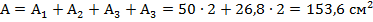
5. Отмечаем положение центра тяжести и координаты каждой фигуры
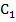 | 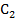 |
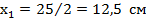 | 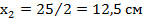 |
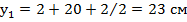 | 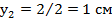 |
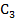 | 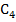 |
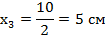 | 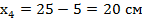 |
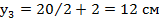 | 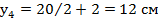 |
6. Статический момент относительно оси
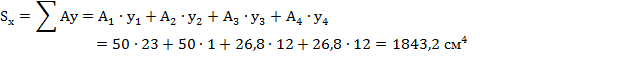
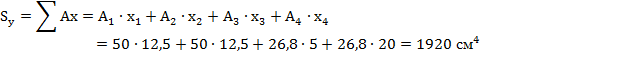
7. Координата точки С

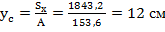
8. На чертеже отмечаем положение точки С (12,5; 12) и через нее проводим центральные (главные) оси 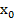 и
и 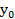
9. Отмечаем на чертеже и вычисляем расстояния от центра тяжести каждой фигуры до центральной оси 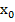 и
и 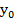
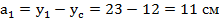 | 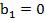 |
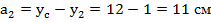 | 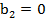 |
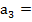 0 0 | 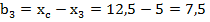 см см |
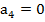 | 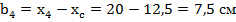 |
10. Осевой момент инерции для каждой фигуры
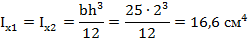

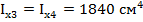
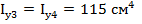
11. Осевой момент инерции относительно главных осей
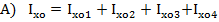
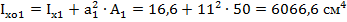
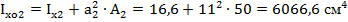

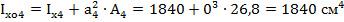
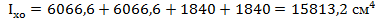

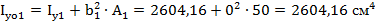
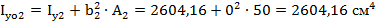
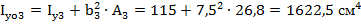
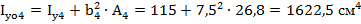
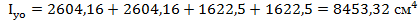
Контрольные вопросы.
1. Что такое статический момент сечения?
Как определяется статический момент сечения относительно нейтральной оси?
2. Чему равен статический момент сечения относительно центральной оси?
3.Что такое осевой момент инерции сечения и в каких единицах он измеряется?
4. Какова зависимость между осевыми моментами инерции относительно параллельных осей?
5. Какие оси, проведенные в плоскости сечения, называются главными? главными центральными?
6. Как определяются осевые моменты инерции сложных составных сечений?
СР №13
