Связь координат вектора и его образа

Вопросы для самоконтроля:

1.Что называется линейным оператором (преобразованием) линейного пространства?

2.Дайте определение матрицы линейного оператора (преобразования) в данном базисе.

3.Как связаны матрицы линейного преобразования в разных базисах?

4.Как найти координаты образа вектора при линейном преобразовании?

5.Что такое сумма, произведение линейных операторов (преобразований), произведение линейного оператора (преобразования) на число?

6.Какова матрица суммы, произведения линейных преобразований?

ВАРИАНТ 1

1.В линейном пространстве A₃ задан оператор φ такой, что для x=(x₁, x₂, x₃): φx=(x₂+x₃, 2x₁+x₃, 3x₁–x₂+x₃). Доказать, что φ – линейный оператор. Найти его матрицы в базисах:

1) e₁=(1,0,0), e₂=(0,1,0), e₃=(0,0,1);

2) a₁=(1,1,1), a₂=(2,1,3), a₃=(4,1,6).

2.Векторы a₁=(2,3,5), a₂=(0,1,2), a₃=(1,0,0) линейным оператором φ преобразуются соответственно в векторы b₁=(1,1,1), b₂=(1,1,-1), b₃=(2,1,2). Найти матрицу этого оператора в том базисе, в котором указаны координаты векторов a_i и b_i, i=1,2,3.

3.Дана матрица М линейного оператора в базисе e₁, e₂, e₃. Найти образы векторов e₁, e₂, e₃, a=2e₁–e₂+3e₃.

.

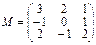ВАРИАНТ 2

1.Показать, что ортогональное проектирование трехмерного пространства V₃ на ось Ox есть линейный оператор. Найти его матрицу в базисе , , .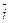

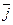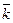2.Линейное преобразование φ в базисе e₁, e₂, e₃ имеет матрицу М. Найти матрицу этого преобразования в базисе e₁’=e₁, e₂’=e₁+e₂, e₃’=e₁+e₂+e₃.

.

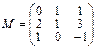3.Линейное преобразование φ:L→L, dimL=2, переводит векторы a₁=(1,3), a₂=(2,1) соответственно в векторы b₁=(0,2), b₂=(1,1). Найти матрицы преобразования φ в базисах:

1) e₁=(1,0), e₂=(0,1);

2) a₁, a₂.

ВАРИАНТ 3

1.Показать, что умножение квадратных матриц второго порядка на матрицу M справа есть линейный оператор. Найти его матрицу в базисе , , , .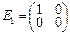

.

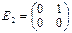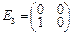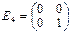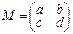2.Пусть φ:L→L, dimL=2 – линейный оператор, имеющий в базисе g₁=(1,2), g₂=(2,3) матрицу М, а линейный оператор η:L→L в базисе u₁=(3,1), u₂=(4,2) задается матрицей N. Найти матрицы линейных операторов φ+η, φ•η в базисе g₁, g₂.

, .

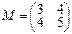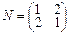3.Матрица М является матрицей линейного оператора φ в базисе e₁, e₂, e₃. Найти образы векторов e₁, e₂, e₃,

a=4e₁–3e₂+e₃.

.

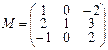ВАРИАНТ 4

1.Дано преобразование φ линейного пространства A₃, которое вектор x=(x₁, x₂, x₃) переводит в вектор φx=(x₁+x₂+x₃, 2x₂, 3x₁–x₃). Доказать, что оно линейное, и найти его матрицы в базисах

1) e₁=(1,0,0), e₂=(0,1,0), e₃=(0,0,1);

2) a₁=(2,3,1), a₂=(0,1,1), a₃=(0,0,3).

2.Дана матрица А линейного преобразования φ пространства многочленов степени не выше 2 в базисе x², x, 1. Найти образ вектора f(x)=x²–4x+3.

.

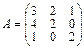3.Преобразование φ в базисе a₁=(-3,7), a₂=(1,-2) имеет матрицу М, а преобразование ψ в базисе b₁=(6,-7), b₂=(-5,6) имеет матрицу N. Найти матрицу φ•ψ в том базисе, в котором даны координаты всех векторов.

, .

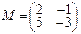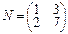ВАРИАНТ 5

1.Преобразование φ пространства многочленов степени не более 3 определяется следующим образом φ(ax³+bx²+cx+d)=ax³+bx²+cx. Доказать, что оно линейно и найти его матрицы в базисах:

1) x³, x², x, 1;

2) x³, x²–3, x+1, 2.

2.Дана матрица A линейного преобразования φ арифметического трехмерного пространства A₃ в базисе a₁=(2,3,0), a₂=(1,1,1), a₃=(0,1,1). Найти:

1) образ вектора b=4a₁+8a₂–a₃;

2) матрицу преобразования φ в базисе e₁=(1,0,0), e₂=(0,1,0), e₃=(0,0,1).

.

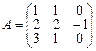3.Линейное преобразование φ в базисе e₁, e₂ имеет матрицу А. Найти матрицу преобразования φ в базисе a₁=2e₁+e₂, a₂=3e₁+e₂.

.

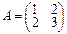ВАРИАНТ 6

1.В пространстве многочленов степени не выше 3 дано преобразование, которое всякий многочлен a₀+a₁x+a₂x²+a₃x³ отображает в многочлен a₀+a₁x+a₂x². Доказать, что преобразование φ линейное и найти его матрицы в базисах:

1) 1, x, x², x³;

2) 1+x, 2–x–x², x²–1, 3x³.

2.Линейное преобразование φ в базисе a₁=(1,2), a₂=(2,3) имеет матрицу А. Линейное преобразование ψ в базисе b₁=(3,1), b₂=(4,2) имеет матрицу B. Найти матрицу преобразования φ•ψ в базисе a₁, a₂.

, .

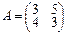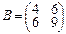3.Дана матрица M линейного преобразования φ в базисе e₁, e₂, e₃. Найти образы векторов e₁, e₂, e₃ и a=4e₁+e₂–e₃.

.

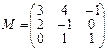ВАРИАНТ 7

1.В пространстве многочленов степени не выше 2 задан оператор φ такой, что φ(f(x))=f(x+1)–f(x). Доказать, что φ– линейный оператор, и найти его матрицы в базисах:

1) x², x, 1;

2) x²+2, 3x–1, 3.

2.Пусть φ:L→L линейный оператор, в базисе g₁=(1,2), g₂=(2,3) имеющий матрицу М, а линейный оператор η:L→L в базисе u₁=(3,1), u₂=(4,2) задается матрицей N. Найти матрицы операторов φ–η, φ•η в базисе u₁, u₂.

, .

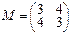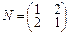3.Дана матрица А линейного преобразования φ в базисе a₁, a₂, a₃. Найти образы векторов a₁, a₂, a₃, b=a₁+2a₃.

.

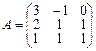ВАРИАНТ 8

1.Найти матрицы оператора дифференцирования пространства многочленов степени не выше 2 в базисах:

1) 1, x, x²;

2) 1, x–1, (x–1)²/2.

2.Найти матрицу линейного преобразования трехмерного пространства A₃, переводящего векторы a₁=(2,3,5), a₂=(0,1,2), a₃=(1,0,0) соответственно в векторы b₁=(1,1,1), b₂=(1,1,-1), b₃=(2,1,2), в том базисе, в котором заданы векторы.

3.Дана матрица М линейного преобразования φ в базисе e₁, e₂. Найти матрицу преобразования φ в базисе a₁=3e₁–e₂, a₂=e₁+e₂.

.

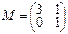ВАРИАНТ 9

1.Дан базис e₁, e₂, e₃, e₄ линейного пространства L, линейный оператор φ:L→L такой, что φe₁=e₁+e₂, φe₂=e₂+e₃, φe₃=e₃+e₄, φe₄=e₄+e₁. Доказать, что векторы g₁=φe₁–φe₂, g₂=φe₂–φe₃, g₃=φe₁+φe₃, g₄=e₄ образуют базис пространства L, и написать матрицу оператора φ в базисе g₁, g₂, g₃, g₄.

2.Пусть линейное преобразование φ в базисе a₁=(0,1), a₂=(1,1) имеет матрицу M, линейное преобразование ψ в базисе b₁=(1,3), b₂=(2,4) имеет матрицу N. Найти матрицу преобразования φ•ψ в базисе a₁, a₂.

, .

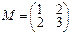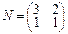3.Матрица C является матрицей линейного преобразования φ в базисе e₁, e₂, e₃. Найти образы векторов e₁, e₂, e₃, a=e₁+3e₂–5e₃.

.

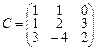ВАРИАНТ 10

1.В линейном пространстве L даны базис e₁, e₂, e₃ и линейный оператор φ:L→L такой, что φe₁=e₁+e₂, φe₂=e₁+e₃, φe₃=e₃+e₂. Доказать, что векторы g₂=φe₂, g₃=φe₃, g₁=φe₁ образуют базис в L, и написать матрицы оператора в базисах:

1) e₁, e₂, e₃;

2) g₁, g₂, g₃.

2.Составить матрицы линейного оператора φ линейного пространства А₃, переводящего векторы x₁=(0,0,1), x₂=(0,0,1), x₃=(1,1,1) соответственно в векторы y₁=(2,3,5), y₂=(1,0,0), y₃=(0,1,-1) в базисах:

1) e₁=(1,0,0), e₂=(0,1,0), e₃=(0,0,1);

2) x₁, x₂, x₃.

3.Линейное преобразование φ в базисе e₁, e₂ имеет матрицу М. Найти образы векторов e₁, e₂, a=3e₁+5e₂.

.

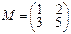ВАРИАНТ 11

1.В линейном пространстве А₃ задан оператор φ такой, что для вектора x=(x₁, x₂, x₃) φx=(x₂+x₃, 2x₁–x₂, x₁+x₃). Доказать, что φ – линейный оператор, и найти его матрицы в базисах:

1) e₁=(1,0,0), e₂=(0,1,0), e₃=(0,0,1);

2) a₁=(1,1,0), a₂=(2,1,3), a₃=(1,1,1).

2.В пространстве многочленов степени не выше 3 даны два оператора:

1) φ: φ(f(x))=f ‘(x);

2) ψ: ψ(ax³+bx²+cx+d)=ax³+bx²+cx.

Найти матрицу оператора φ•ψ в базисе x³, x², x, 1.

3.Матрица М является матрицей линейного преобразования φ в базисе e₁, e₂, e₃. Найти образы векторов e₁, e₂, e₃, a=3e₁–2e₂+e₃.

.

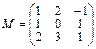ВАРИАНТ 12

1.Проверить, что транспонирование квадратных матриц второго порядка есть линейный оператор. .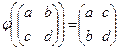

Найти матрицу этого оператора в базисе

, , , .

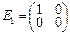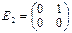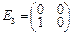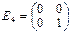2.Линейное преобразование φ: L→L в базисе e₁, e₂ имеет матрицу М. Найти его матрицу в базисе a₁=e₁+2e₂, a₂=2e₂+3e₃.

.

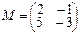3.Линейное преобразование φ: L→L переводит векторы a₁=(2,0,3), a₂=(4,1,5), a₃=(3,1,2) соответственно в векторы b₁=(1,2,-1), b₂=(4,5,-2), b₃=(1,1,1). Найти матрицу этого преобразования в том базисе, в котором даны координаты всех векторов.

ВАРИАНТ 13

1.Доказать, что преобразование φ линейного пространства А₃, переводящее вектор x=(x₁, x₂, x₃) в вектор φx=(x₁+x₂, x₂+3x₃, 3x₃), является линейным. Найти матрицы преобразования φ в базисах:

1) e₁=(1,0,0), e₂=(0,1,0), e₃=(0,0,1);

2) a₁=(2,2,-1), a₂=(1,1,0), a₃=(3,0,0).

2.Матрица M является матрицей линейного преобразования φ в базисе a₁=(1,2), a₂=(3,0). Матрица N является матрицей линейного преобразования ψ в базисе e₁=(1,0), e₂=(0,1). Найти матрицы преобразований φ+ψ и φ•ψ в базисе a₁, a₂.

, .

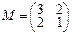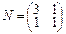3.Матрица А является матрицей линейного преобразования φ в базисе e₁, e₂, e₃. Найти образы векторов e₁, e₂, e₃, x=3e₁+2e₂+e₃.

.

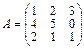ВАРИАНТ 14

1.В пространстве многочленов степени не выше 2 дано преобразование φ такое, что φ(ax²+bx+c)=ax²+bx. Доказать, что φ – линейное преобразование, и найти его матрицы в базисах:

1) x², x, 1;

2) x²+2x–1, x–1, 2.

2.Линейный оператор φ в базисе a₁=(3,1), a₂=(4,2) имеет матрицу M, линейный оператор ψ в базисе b₁=(1,2), b₂=(2,3) имеет матрицу N. Найти матрицы операторов φ+ψ, φ•ψ в базисе b₁, b₂.

, .

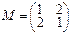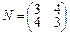3.Линейный оператор φ переводит векторы a₁=(1,2),

a₂=(2,-1) соответственно в векторы b₁=(3,1), b₂=(2,1).

Найти матрицу оператора φ в том базисе, в котором даны

координаты всех векторов.

Лабораторная работа 11