Характеристические уравнения для дифференциальных уравнений второго порядка
Тема 1. Классификация дифференциальных уравнений второго порядка в частных производных.
Для упрощения записей ограничимся случаем двух переменных.
Пусть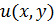 
- искомая функция. Ограничиваясь случаем производных, не выше второй степени будем считать заданным некий функционал
,
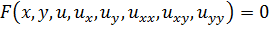где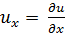 
; 
; 
; 
; 
.
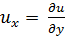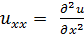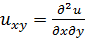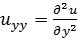1.1 Линейное дифференциальное уравнение второго порядка
в частных производных.
Введем более простое уравнение:
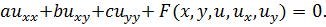(1.1)
Оно линейно по старшим производным, если коэффициенты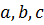 
зависят только от (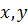 
) и не зависят от 
.
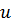Введем уравнение
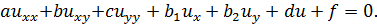(1.2)
Если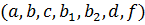 
– зависят только от ( 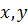), то уравнение (1.2) линейно.
Если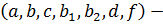 
const, то уравнение называется линейным дифференциальным уравнением (ДУ) с постоянными коэффициентами.
Если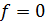 
, то (1.2) – линейное однородное уравнение. Нашей дальнейшей целью является упрощение формы ДУ путем подбора других систем координат.
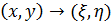, где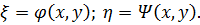 
Новые координаты выбираются так, чтобы соответствующий определитель
.
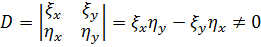Лемма 1. При переходе к новой системе координат линейное уравнение остается линейным. Нужно доказать, что (1.1) перейдет в некоторое линейное уравнение:
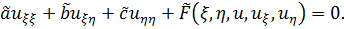(1.1’)
Три типа дифференциальных уравнений второго порядка в частных производных
Для уравнений (1.1),(1.1’) введем некоторую величину, называемую дискриминантом
Для уравнения (1.1)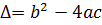 
, (1.4)
Для уравнения (1.1’)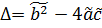 
. (1.4’)
Лемма 2. При смене системы координат знак 
не меняется, если определитель преобразования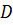 
не обращается в ноль:
.
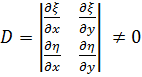Если в какой-то области дискриминант имел определенный знак, то он сохранит тот же знак в области, полученной из данной преобразованием координат,при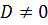 
.
Будем называть уравнения в той области, где
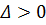– гиперболическими,
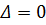– параболическими,
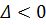– эллиптическими.
Рассмотрим условия, когда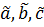 
обращаются в ноль.
Характеристические уравнения для дифференциальных уравнений второго порядка
Новые координаты приводят к изменению коэффициентов
,
.
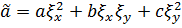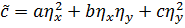Лемма 3. Если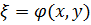 
является частным решением уравнения
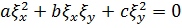, (1.5)
то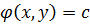 
, где c = const является общим интегралом уравнения:
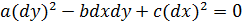. (1.6)
Лемма 4. Если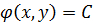 
является общим интегралом уравнения (1.6), то 
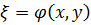- частное решение (1.5).
| Рис. 3 |
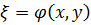, где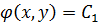 
- общий интеграл для (1.6), чтобы 
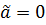. Аналогичным образом, если у нас есть еще один общий интеграл для (1.6),
t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>C</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>2</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">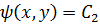 
,то его примем за новую переменную, чтобы 
.
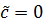Для характеристического уравнения
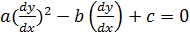получаем
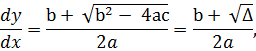
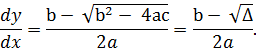
1) Для гиперболических уравнений (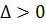 
) существуют 2 решения (2 общих интеграла) для (1.6).
Выбираем , .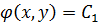
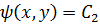Тогда можем обеспечить уничтожаемость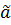 
и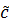 
.
2) Для параболических уравнений (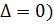 
имеется одно решение (один общий интеграл) для (1.6).
Выберем его за одну новую переменную 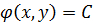, исключается только 
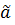или .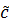
3) Для эллиптических уравнений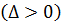 
есть два комплексных решения характеристического уравнения.
За новые переменные можно взять их действительную и мнимую части.