Неопределенные и определенные интегралы

171 – 180. Закон движения точки на прямой задан функцией S(t). Найти скорость V(t) и ускорение a(t) и их наибольшие абсолютные значения на отрезке [ 0 ; T ].

171. 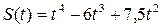, Т=3.

173. 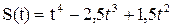, Т=1.

175. 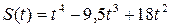, Т=5.

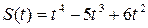
177. , Т=3.

179. 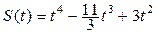, Т=2.

172. 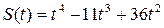, Т=3.

174. 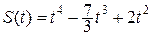, Т=1.

176. 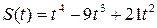, Т=4.

178. 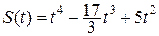, Т=3.

180. 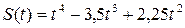, Т=2.

181 – 190. Найти неопределённые интегралы.

181. а) ,

в) ,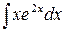

д) ,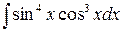

б) ,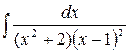

г) ,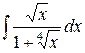

е) .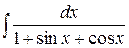

182. а) ,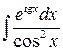

в) ,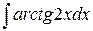

д) ,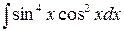

б) ,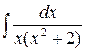

г) ,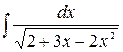

е) .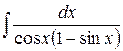

183. а) ,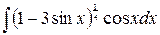

в) ,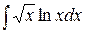

д) ,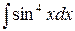

б) ,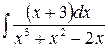

г) ,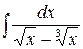

е) .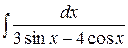

184. а) ,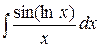

в) ,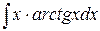

д) ,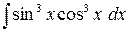

б) ,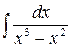

г) ,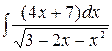

е) .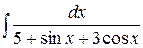

185. а) ,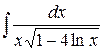

в) ,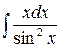

д) ,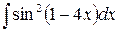

б) ,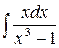

г) ,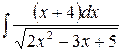

е) .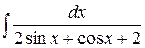

186. а) ,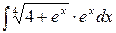

в) ,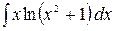

д) ,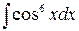

б) ,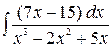

г) ,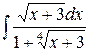

е) .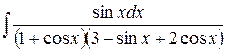

187. а) ,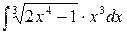

в) ,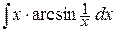

д) ,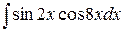

б) ,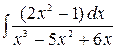

г) ,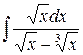

е) .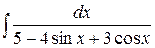

188. а) ,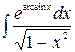

в) ,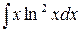

д) ,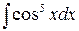

б) ,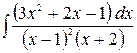

г) ,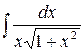

е) .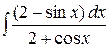

189. а) ,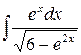

в) ,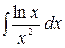

б) ,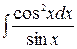

г) ,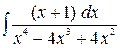

д) ,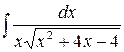

е) .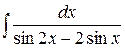

190. а) ,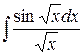

в) ,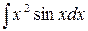

д) ,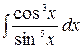

б) ,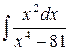

г) ,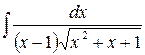

е) .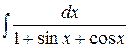

191 – 200. Вычислить определённый интеграл.

191. .

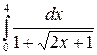193. .

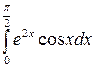195. .

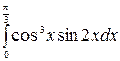197. .

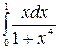199. .

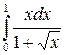192. .

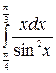194. .

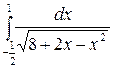196. .

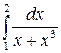198. .

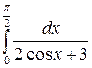200. .

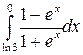201 – 210.

201. Вычислить площадь фигуры, ограниченной параболой 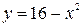и полукубической параболой .

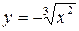202. Вычислить площадь фигуры, ограниченной кардиоидой .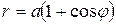

203. Вычислить площадь фигуры, ограниченной трёхлепестковой розой .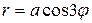

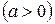204. Вычислить площадь фигуры, ограниченной одной аркой циклоиды 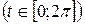и осью Ох.

205. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями , .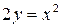

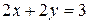206. Вычислить объём тела, образованного вращением вокруг оси Оy астроиды , .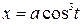

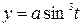207. Вычислить длину дуги кривой 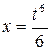, 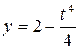между точками её пересечения с осями координат.

208. Вычислить длину дуги одной арки циклоиды , .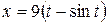

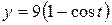209. Вычислить длину дуги полукубической параболы 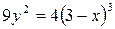между точками пересечения с осью Оу.

210. Вычислить длину кардиоиды , .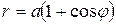

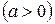211 – 220. Вычислить несобственный интеграл или доказать его расходимость.

211. .

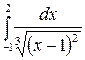213. .

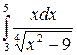215. .

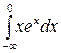217. .

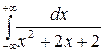219. .

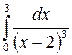212. .

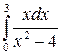214. .

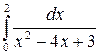216. .

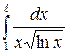218. .

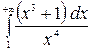220. .

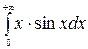Методические указания к выполнению контрольных работ

Контрольная работа №1

Запишем формулы для вычисления определителей второго и третьего порядка:

,

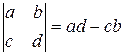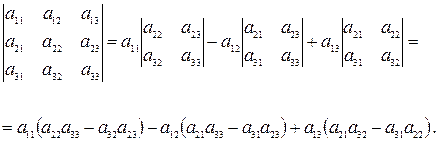
Примеры. .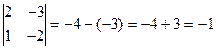

.

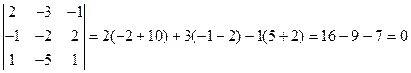Некоторые формулы векторной алгебры (1210)

1) Если 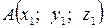, , 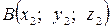то

.

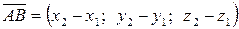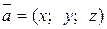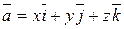2) Если , то и

.

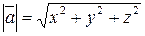3) Скалярным произведением векторов 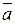и 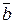называется число 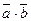, равное произведению модулей этих векторов и косинуса угла 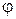между этими векторами:

.

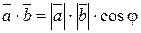Если известны координаты векторов

, ,

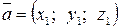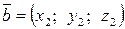то

,

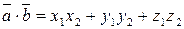угол 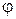между векторами определяется формулой

.

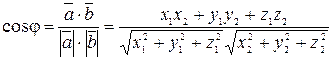4) Векторным произведением векторов 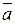и 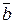называется вектор 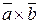, перпендикулярный векторам 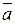и 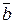, модуль которого равен площади параллелограмма, построенного на векторах 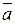и 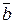, и направленный так, что из его конца кратчайший поворот от вектора 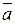к вектору 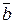наблюдается происходящим против часовой стрелки.

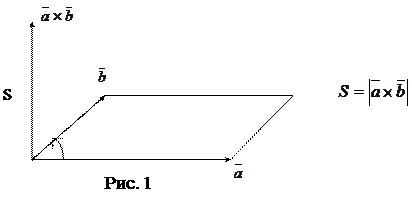Если известны координаты векторов 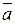и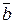

, ,

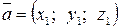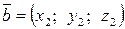то векторное произведение выражается через определитель третьего порядка:

.

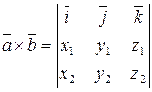Площади параллелограмма и треугольника, построенных на векторах 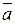и :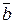

, .

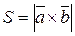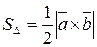5) Смешанным произведением векторов 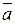, , 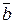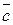называется число

.

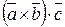Если известны координаты векторов

, , ,

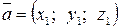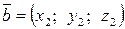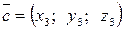то .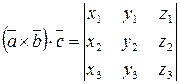

Смешанное произведение, взятое по абсолютной величине, равно объему параллелепипеда, построенного на векторах 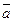, , 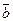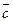. Объем пирамиды, построенной на этих векторах, составляет шестую часть объема параллелепипеда.

V_{параллелепипеда} ,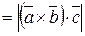

V_{пирамиды} .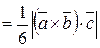

Примеры. ,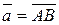

; .

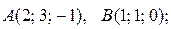
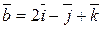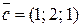Тогда

,

,

.

,

,

;

;

;

;

.
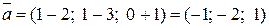
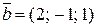
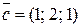
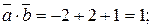
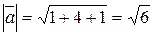
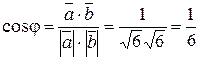
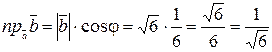
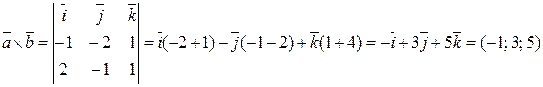
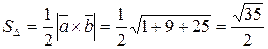
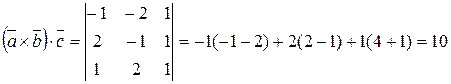
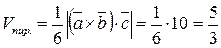