Расчетно-графическая работа №10

«Расчет на прочность круглого бруса при совместном действии изгиба и кручения»

Теоретическое обоснование. Сочетание деформаций изгиба и кручения испытывает большинство валов, которые обычно представляют собой прямые брусья круглого или кольцевого сечения.

Максимальные нормальные и касательные напряжения у круглых валов вычисляют по формулам

Причём для круглых валов

При сочетании изгиба и кручения опасными будут точки опасного поперечного сечения вала, наиболее удаленные от нейтральной оси.

Применив третью теорию прочности, гипотеза наибольших касательных напряжений получим

Формула для определения эквивалентного момента

По энергетической теории прочности

где W – осевой момент сопротивления сечения

По найденному значению W и принятому виду сечения (круг или кольцо) вычисляют необходимый диаметр вала.

Расчётным, или опасным, сечением является то, в котором возникают максимальные изгибающий и крутящий моменты. Иногда приходится проводит расчёт для нескольких сечений, так как в общем случае максимальные изгибающий и крутящий моменты возникают в различных поперечных сечениях вала. Расчётная формула для круглых валов принимает вид

(валы обычно изготовляют из материала, у которого

По этой формуле расчёт круглых валов ведут, как на изгиб, но не по изгибающему, а по эквивалентному моменту.

Алгоритм решения

1. Привести действующие на вал нагрузки к его оси

2. Освободить вал от опор, заменив их действие реакциями в вертикальной и горизонтальной плоскостях (т. е. получить расчетную схему)

3. По заданной мощности и угловой скорости определить вращающие моменты, действующие на вал

4. Составить уравнения равновесия всех сил, действующих на вал, отдельно в вертикальной и отдельно в горизонтальной плоскости. Определить нагрузки, приложенные к валу

5. Построить эпюру крутящих моментов

6. Определить наибольшее значение эквивалентного момента

или

7. Приняв , определить требуемую величину осевого момента сопротивления

8. Из выражения определить d – диаметр вала, округлив его значение (в мм) в большую сторону до целого чётного числа или числа, оканчивающегося на 5

Вариант А Для стального вала постоянного поперечного сечения с одним зубчатым колесом, передающего мощность и : а) определить вертикальные и горизонтальные составляющие реакции подшипников; б) построить эпюру крутящих моментов; в) построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях; г) определить диаметр вала, приняв Для усилий, действующих на зубчатое колесо, принять . В задах четного варианта расчет производить по гипотезе потенциальной энергии формоизменения, а в задачах нечетного варианта – по гипотезе наибольших касательных напряжений.

Вариант Б Для стального вала постоянного поперечного сечения, передающего мощность при угловой скорости : а) определить вертикальные и горизонтальные составляющие реакции подшипников; б) построить эпюру крутящих моментов; в) построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях; г) определить диаметр вала, приняв Принять . В задах четного варианта расчет производить по гипотезе наибольших касательных напряжений, а в задачах нечетного варианта – по гипотезе потенциальной энергии формоизменения.

ЗАДАНИЕ

ЗАДАЧА

Вар	№ схемы	кВт	ω рад/с	вар	№ схемы	P кВт	ω рад/с	вар	№ схемы	P кВт	ω рад/с	вар	№ схемы	P кВт	ω рад/с
						42,0	16,4							35,6	18,6
						14,3	29,3							37,2	14,0
						13,3	24,8							44,4	14,4
						29,2	22,2							29,0	22,0
						21,6	45,6							44,4	28,0
		14,5	12,0							33,0	18,4
		17,2	17,4							24,2	19,0
		18,0	18,8							24,8	10,0
		28,4	20,4							15,0	19,8
		35,0	35,0							27,2	15,0

Пример выполнения

Задача

Для стального вала круглого поперечного сечения с одним зубчатом колесом передающая мощность 12 кВт при угловой скорости 40 .

Определить диаметр вала в опасном сечении приняв .

Решение.

1)Определяем вращающий момент.

Нм

2)Определяем окружную силу.

Н

3)Определяем радиальную силу.

Н

4)Составляем расчетную схему, определяем опорные реакции и строим эпюру момента изгибающего от вертикальной силы .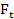

кН

кH

Проверка:

Момент изгибающий определяем по характерным точкам.

Рассматриваю вал слева направо.

Н

5)Составляем расчетную схему, определяем опорные реакции и строим эпюру момента изгибающего горизонтальной силы .

кH

к5H

Проверка:

Момент изгибающий определяем по характерным точкам.

Рассматриваю вал слева на право.

Н

6)Значение момента крутящего в любом сечении вала определяется:

Нм

Строим эпюру момента крутящего.

7)Из эпюр изгибающих и крутящих моментов следует, что опасное сечение вала проходит через точку А.

8)Определяем наибольшее значение эквивалентного момента (по третьей гипотезе прочности)

Нм

9)Из условия гипотезы прочности

из ее правой части

определяем диаметр вала:

мм

Контрольные вопросы.

1. Какие внутренние силовые факторы возникают в поперечном сечении деталей, работающих на совместное действие изгиба и кручения?

2. Что такое гипотезы прочности и в каких случаях возникает возможность их применения?

3. Как производится расчет валов на прочность при совместном действии изгиба и кручения?

4. Что такое эквивалентный момент и как его определить?

5. Что такое суммарный изгибающий момент?

6. Что такое эквивалентное напряжение?

7. Какой вид имеет выражение эквивалентного напряжения при совместном действии изгиба и кручения по гипотезе потенциальной энергии формоизменения?

СР.№16