ПРИМЕР РЕШЕНИЯ ЗАДАЧИ № 8

Короткий чугунный брус с заданным поперечным сечением (рисунок 34) сжи­­мается силой Р, приложенной в точке D. Определить из условия проч­нос­ти бруса допускаемое значение силы Р_д .

Числовые данные к задаче: a = 0,08м; b = 0,12м; a = 0,5; пределы прочности чугуна при растяжении s_вр = 280МПа, при сжатии

s_вс= 1000 МПа; запас прочности принять n = 1,5.

1.Определение геометрических характеристик поперечного сечения.

Заданное сечение (рисунок 34) рассматриваем как сложное, состоящее из двух прямоугольников: большого сплошного со сторонами a и b и прямо­угольного отверстия со сторонами 0,5 a и 0,6 b.

За исходные координатные оси принимаем оси к z₁ и y. На рисунок34 в этой системе координат показаны положения центров тяжести прямо­угольников (точки С₁ и С₂) и их главные центральные оси y₁,_,z₁, y₂, z₂. Центр тяжести всего сече­ния обозначен через O. Он располагается на оси сим­метрии у, поэ­тому вычисляется только одна его коор­ди­ната у_C :

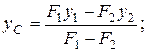
где F₁ и F₂ - площади боль­шого прямо­уго­ль­ни­ка и отверстия;

y₁ и y₂ - координаты ­­­­ их центров тяжести.

Подсчитываем геометрические характеристики поперечного сечения бруса.

Площади составляющих фигур

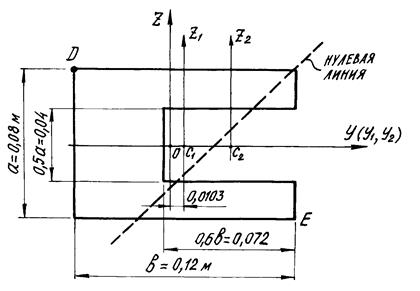Рисунок 34 - Поперечное сечение бруса

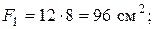
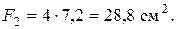
Площадь сечения всей фигуры:

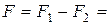
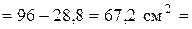
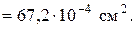
Абсциссы центров тя­же­с­ти составляющих фи­гур:

y₁ = 0; y₂ = 2,4см.

Абсцисса центра тя­же­сти всей фигуры:

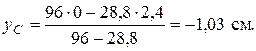
Центр тяжести сечения лежит на оси Y (точка О) слева от точки С₁ на расстоянии y_с. Главные центральные оси сечения - Y, Z.

Главные центральные моменты инерции составного сечения относи­тельно осей Y, Z вычисляются с помощью зависимостей между моментами инерции отно­сительно параллельных осей, одна из которых центральная:

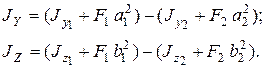
Моменты инерции прямоугольников относительно собственных глав­ных центральных осей равны

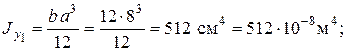
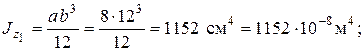
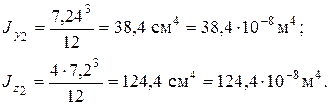
Расстояния между главными центральными осями Y, Z и собственными глав­ными центральными осями составляющих фигур определяются по чер­тежу.

Расстояние между главной центральной осью Y и осями y₁,y₂:

a₁ = а₂ = 0, так как глав­ные центральные оси у₁ и y₂ составляющих фи­гур совпадают с главной центральной осью Y сечения;

расстояния между главной центральной осью Z и осями z₁, z₂:

b₁ = 1,03 см,

b₂ = 1,03 + 2,4 =3,43 см .

Подставив найденные величины в формулы для вычисления главных цент­ральных моментов инерции и учитывая, что осевой момент инерции от­вер­стия условно считается отрицательным, получаем

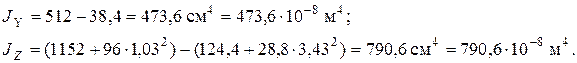
Квадраты главных центральных радиусов инерции

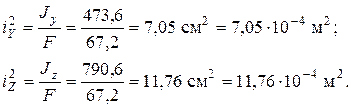
2.Определение положения нулевой линии.

По условию задачи сила Р приложена в точке D, координаты которой в си­стеме главных центральных осей Y, Z определяются по рисунку 34:

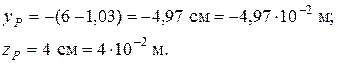
Отрезки, отсекаемые нулевой линией на осях координат Y, Z:

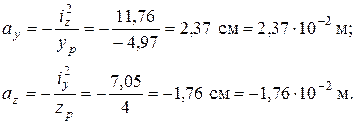
На осях координат Y, Z откладываются в масштабе величины найденных отрезков и проводится нулевая линия.

3. Вычисление максимальных нормальных напряжений в поперечном сече­нии бруса.

Максимальные напряжения возникают в точках, наиболее удаленных от ну­левой линии. В рассматриваемой задаче это точки D и E. В точке D на­пря­жения сжимающие, в точке E - растягивающие.

Координаты опасных точек находятся по рисунку 34:

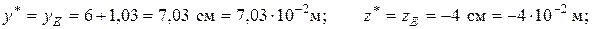
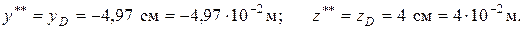
Максимальные растягивающие и сжимающие напряжения выражаются че­рез внешнюю нагрузку;

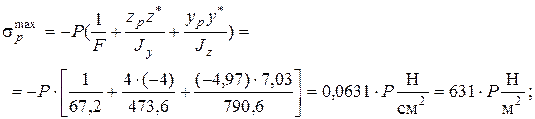
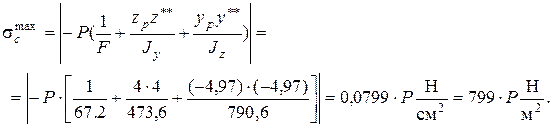
Допускаемая нагрузка Р_доп определяется из условий прочности бруса по растягивающим и сжимающим напряжениям.

Допускаемые напряжения определяются по исходным данным для растяжения и для сжатия хрупкого материала, в рассматриваемом случае чугуна:

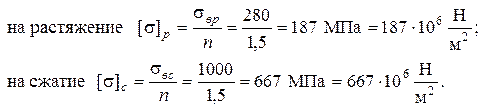
Из условия прочности материала бруса на растяжение 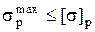опре­де­ляется величина допускаемой нагрузки

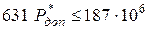, откуда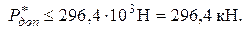

Из условия прочности на сжатие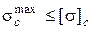

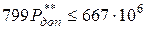и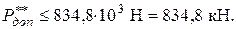

В качестве допускаемой нагрузки принимается меньшая из двух полу­чен­ных, что обеспечивает прочность бруса как по растягивающим, так и по сжи­­мающим напряжениям, то есть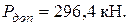

ЗАДАЧА № 9

Для стального стержня длиной l, cжимаемого силой Р,требуется:

1) подобрать размеры поперечного сечения стержня из условия его устойчивости при допускаемом напряжении на сжатие [s] = 160 МПа (расчет проводить методом последовательных приближений по коэффи­циенту снижения допускаемых напряжений на сжатие);

2) найти величину критической силы и коэффициент запаса устойчивости n_у.

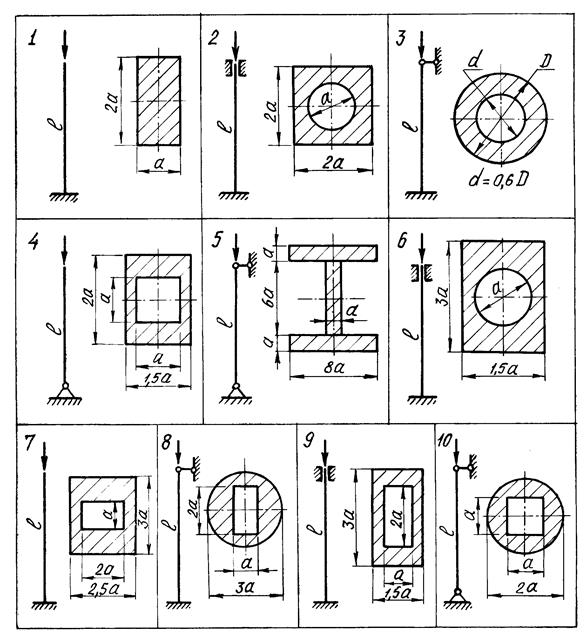Рисунок 35 - Расчетные схемы сжатых стержней и их поперечные сечения

Числовые данные для расчета следует взять из табл.15, расчетные схемы - по рисунку 35.

Таблица 9 -Числовые данные к задаче №9