Истечение жидкости через насадки
Насадком называется короткая труба, присоединенная к отверстию в тонкой стенке. Насадки имеют различные формы живого сечения и постоянные или меняющиеся размеры основного канала по длине.
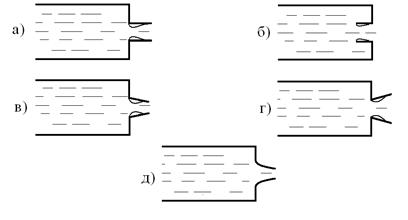
Рис. 10.5. Истечение жидкости через насадки раздичной формы
Насадки играют большую роль в современной технике. Их применяют для увеличения расхода жидкости через отверстие, измерения расхода жидкости, организации направленного слива, создания струй, имеющих самое различное назначение и применение. Так, например, струями высокого давления разрушаются твердые горные породы и режутся металлы.
На рис. 10.5 показаны наиболее распространенные типы насадков: а - наружный цилиндрический насадок (насадок Вентури); б - внутренний цилиндрический (насадок Борда); в - конический сходящийся насадок; г - конический расходящийся насадок; д — коноидальный насадок, выполненный в форме вытекающей струи.
Струя жидкости, поступающая в насадок, в большинстве случаев отрывается от стенки насадка у входа благодаря силам инерции частиц жидкости, движущихся по криволинейным траекториям (рис. 10.6); затем струя расширяется и на выходе заполняет весь насадок. В области отрыва струи от стенок насадка создается пониженное давление, которое как бы дополнительно подсасывает жидкость и тем самым увеличивает ее расход.
Рассмотрим сначала истечение жидкости через внешний цилиндрический насадок (рис. 10.6).
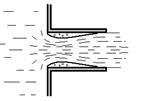
Рис. 10.6. Отрыв струи при входе в насадок
Струя жидкости при входе в насадок сжимается, затем постепенно расширяется и заполняет все сечение насадка. Так как выходное сечение насадка полностью заполнено жидкостью, то коэффициент сжатия струи равен 1, а коэффициент расхода
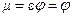 ,
, 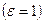 .
.
Таким образом, для этого насадка коэффициент расхода равен коэффициенту скорости.
Составим уравнение Бернулли для жидкости, находящейся между сечениями 1 - 1 и 2 - 2 (рис. 10.7):
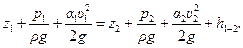
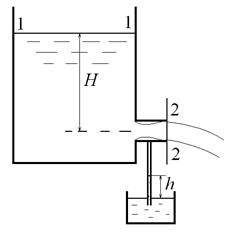
Рис. 10.7. Расчет истечения жидкости из резервуара через отверстие с внешним цилиндрическим насадком
Так же, как при истечении из отверстия, будем считать, что 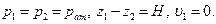 Из уравнения Бернулли получим:
Из уравнения Бернулли получим:
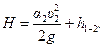 (10.14)
(10.14)
Потери напора 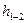 складываются из местных потерь напора при входе жидкости в насадок и потерь на расширение струи внутри насадка, т. е.
складываются из местных потерь напора при входе жидкости в насадок и потерь на расширение струи внутри насадка, т. е.
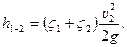
Подставив это выражение в формулу (10.14), найдем скорость 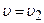 истечения жидкости из насадка:
истечения жидкости из насадка:
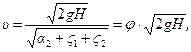
где
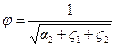 .
.
Для расхода 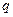 жидкости получим соотношение
жидкости получим соотношение
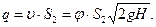
Здесь коэффициент скорости 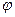 равен коэффициенту расхода
равен коэффициенту расхода 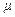 .
.
Отметим, что при истечении жидкости через насадки, так же как и при истечении через отверстия, все коэффициенты истечения в общем случае зависят от числа Рейнольдса. Однако при больших числах Рейнольдса коэффициент расхода 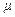 перестает зависеть от числа Рейнольдса и становится практически постоянной величиной, равной
перестает зависеть от числа Рейнольдса и становится практически постоянной величиной, равной 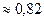 .
.
Сравним истечение жидкости через отверстие в тонкой стенке с истечением жидкости через внешний цилиндрический насадок. При истечении жидкости через насадок в область с атмосферным давлением скорость 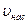 и расход
и расход 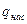 определяются формулами:
определяются формулами:
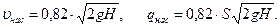 (10.15)
(10.15)
В случае истечения жидкости через отверстие в тонкой стенке скорость 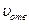 и расход
и расход 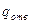 выражаются формулами:
выражаются формулами:
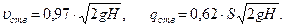 (10.16)
(10.16)
Если величины 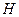 и
и 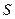 сравниваемых насадка и отверстия считать одинаковыми, то
сравниваемых насадка и отверстия считать одинаковыми, то
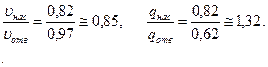
Как видно, внешний цилиндрический насадок увеличивает расход жидкости примерно на 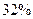 и уменьшает скорость ее истечения примерно на 15%.
и уменьшает скорость ее истечения примерно на 15%.
Скорость жидкости в сжатом сечении насадка больше скорости жидкости на выходе из него, следовательно, давление внутри насадка, в сжатом сечении, меньше, чем давление на его выходе. Поскольку давление на выходе из насадка равно атмосферному, то внутри насадка давление меньше атмосферного; иными словами, там существует вакуум. Наличие этого вакуума объясняет увеличение расхода жидкости при истечении через насадок по сравнению с истечением жидкости без него.
Существование области вакуума внутри насадка можно продемонстрировать следующим опытом. Если в месте наибольшего сжатия струи подсоединить к насадку стеклянную трубку, опущенную другим концом в открытый сосуд с жидкостью (рис. 10.7), то можно наблюдать, как жидкость поднимется по трубке на некоторую высоту, что подтверждает образование в насадке вакуума. Благодаря вакууму насадок работает как своеобразный насос, дополнительно подсасывающий жидкость.
Уменьшение скорости жидкости на выходе из насадка можно объяснить увеличением потерь напора в связи с расширением струи внутри насадка.
Отметим, что не всякий внешний цилиндрический насадок работает с коэффициентом расхода 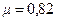 . Иногда можно наблюдать явление, называемое срывом струи, т.е. такое истечение, в котором струя жидкости отрывается от стенок насадка по всей его длине (рис. 10.8). Разумеется, в этом случае, нельзя получить увеличение расхода, описанное выше.
. Иногда можно наблюдать явление, называемое срывом струи, т.е. такое истечение, в котором струя жидкости отрывается от стенок насадка по всей его длине (рис. 10.8). Разумеется, в этом случае, нельзя получить увеличение расхода, описанное выше.
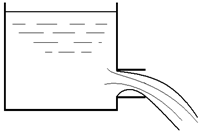
Рис. 10.8. Срыв струи жидкости при истечении через насадок
Для того чтобы внешний цилиндрический насадок действительно увеличивал расход, необходимо выполнение двух условий: 1) Длина 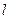 насадка должна лежать в пределах
насадка должна лежать в пределах 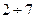 его диаметров
его диаметров 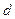 . Если
. Если 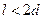 , то струя жидкости не успевает расшириться и занять все сечение насадка, поэтому насадок будет работать неполным сечением и расход уменьшится. Если
, то струя жидкости не успевает расшириться и занять все сечение насадка, поэтому насадок будет работать неполным сечением и расход уменьшится. Если 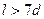 , то уже нельзя пренебрегать потерями напора по длине насадка, и расход также не увеличится; 2) Величина вакуума в сжатом сечении насадка не должна превышать некоторого максимального значения
, то уже нельзя пренебрегать потерями напора по длине насадка, и расход также не увеличится; 2) Величина вакуума в сжатом сечении насадка не должна превышать некоторого максимального значения 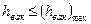 , например, для воды
, например, для воды 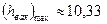 м.
м.
Для определения величины вакуума в сжатом сечении струи внутри насадка запишем уравнение Бернулли для жидкости, заключенной между сжатым сечением струи ( 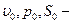 скорость жидкости, давление и площадь сжатого сечения струи, соответственно) и выходным сечением 2 – 2 насадка, рис.10.7. Имеем:
скорость жидкости, давление и площадь сжатого сечения струи, соответственно) и выходным сечением 2 – 2 насадка, рис.10.7. Имеем:
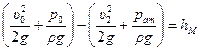 , (10.16)
, (10.16)
где 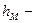 местные потери напора при внезапном расширении струи. Согласно теореме Борда-Карно (см.п.5, гл. 4), эти потери выражаются формулой
местные потери напора при внезапном расширении струи. Согласно теореме Борда-Карно (см.п.5, гл. 4), эти потери выражаются формулой
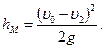 (10.17)
(10.17)
Подставив (10.17) в уравнение (10.16), получим:

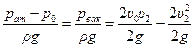
или
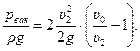 (10.18)
(10.18)
Поскольку из уравнения неразрывности следует, что расход жидкости в установишемся течении постоянен, т.е. 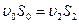 , то
, то
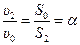 ,
,
следовательно:
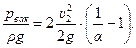 (10.19)
(10.19)
Если учесть соотношение (10.15) и принять, что коэффициент сжатия струи в насадке приближенно равен коэффициенту сжатия струи при истечении из отверстия в тонкой стенке (т.е. 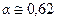 ), то
), то
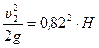 ,
,
и далее, вакуумметрический напор 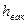 в сжатом сечении струи выражается через движущий напор
в сжатом сечении струи выражается через движущий напор 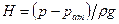 насадка:
насадка:
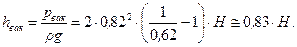 (10.20)
(10.20)
Таким образом, вакуумметрическая высота 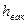 в насадке составляет величину
в насадке составляет величину 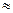
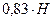 . Вместе с тем, она не может беспредельно увеличиваться вместе с движущим напором
. Вместе с тем, она не может беспредельно увеличиваться вместе с движущим напором 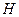 ; поскольку при
; поскольку при 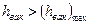 происходит срыв струи, и подсасывающий эффект исчезает. Следовательно, существует максимальное значение
происходит срыв струи, и подсасывающий эффект исчезает. Следовательно, существует максимальное значение 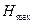 , при котором срыв струи не происходит. Например, для воды
, при котором срыв струи не происходит. Например, для воды 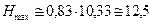 м.
м.
Явления, происходящие во внутреннем цилиндрическом насадке, аналогичны явлениям во внешнем насадке. Отличается внутренний насадок от внешнего насадка большим сопротивлением на входе, поэтому и сжатие струи на входе получается также большим. Отсюда следует, в частности, что скорость и величина вакуума в сжатом сечении струи у внутреннего насадка больше, чем у внешнего насадка. Так, например, в опытах с водой при больших числах 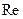 для внутреннего цилиндрического насадка получены значения:
для внутреннего цилиндрического насадка получены значения:
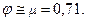 (10.21)
(10.21)
В коническом сходящемся насадке сжатие струи на входе меньше, чем в наружном цилиндрическом насадке, однако имеется существенное сжатие струи на выходе из насадка. Потери напора в этом насадке меньше, чем в наружном цилиндрическом насадке, т. к. сжатие струи меньше, а значит скорость на выходе больше. Коэффициенты расхода и скорости истечения зависят от угла конусности насадка.
В коническом расходящемся насадке сжатие струи значительно больше, чем в предыдущих насадках: коническом сходящемся и цилиндрическом, однако сжатие струи на выходе из расходящегося насадка практически отсутствует. Расход жидкости в коническом расходящемся насадке значительно больше, чем в наружном цилиндрическом насадке, а скорость в выходном сечении значительно меньше.
Коноидальные насадки имеют форму струи жидкости, вытекающей из отверстия. Внутреннее сжатие струи наименьшее, внешнее сжатие практически отсутствует. Коэффициенты скорости 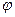 и расхода
и расхода 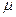 больше, чем во всех случаях, рассмотренных выше. Так, например, в экспиментах, выполненых на воде при больших числах Рейнольдса получено:
больше, чем во всех случаях, рассмотренных выше. Так, например, в экспиментах, выполненых на воде при больших числах Рейнольдса получено: 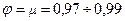 .
.
