Простейшие свойства групп.

17.
В любой группе выполняется закон сокращения: 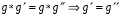(левый закон сокращения; аналогично, имеет место и правый закон). Доказательство. Домножим равенство слева на 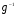и воспользуемся свойством ассоциативности: .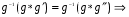

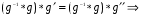
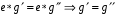18.
Признак нейтрального элемента: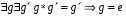

Доказательство Применим к равенству 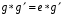закон сокращения.

19.
Признак обратного элемента: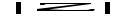

Доказательство: Применим закон сокращения к равенству .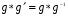

20.
Единственность обратного элемента. Обратный элемент определен однозначно. Следует из п.3.

21.
Существование обратной операции. Для любых двух элементов 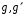произвольной группы G уравнение 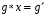имеет и притом единственное решение. Доказательство Непосредственно проверяется, что 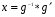(левое частное элементов 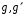) является решением указанного уравнения. Единственность вытекает из закона сокращения, примененного к равенству 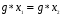. Аналогично устанавливается существование и единственность правого частного.

Изоморфизм групп.

Определение.

Отображение 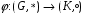двух групп G и K называется изоморфизмом , если

1.Отображение взаимно однозначно. 2.Отображение сохраняет операцию: .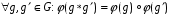

Поскольку отображение обратное к также является изоморфизмом, введенное понятие симметрично относительно групп G и K , которые называются изоморфными.

Примеры.

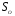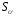1.Группы поворотов плоскости и вокруг точек 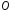и 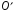изоморфны между собой. Аналогично, изоморфными будут и группы, состоящие из поворотов пространства относительно любых двух осей.

2.Группа диэдра 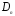и соответствующая пространственная группа 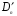изоморфны.

22.
Группа тетраэдра T изоморфна группе 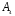состоящей из четных подстановок четвертой степени. Для построения изоморфизма достаточно занумеровать вершины тетраэдра цифрами 1,2,3,4 и заметить, что каждый поворот, совмещающий тетраэдр с собой некоторым образом переставляет его вершины и, следовательно, задает некоторую подстановку множества{1,2, 3, 4} Повороты вокруг оси, проходящей через некоторую вершину (например 1), оставляет символ 1 на месте и циклически переставляет символы 1, 2, 3. Все такие перестановки - четные. Поворот вокруг оси, соединяющей середины ребер (например, 12 и 34 ) переставляет символы 1 и 2 , а также 3 и 4. Такие перестановки также являются четными.

23.
Формула 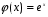определяет взаимно однозначное соответствие между множеством R вещественных чисел и множеством 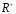положительных чисел. При этом 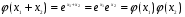. Это означает, что 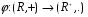является изоморфизмом.

Замечание. В абстрактной алгебре изоморфные группы принято считать одинаковыми. По существу это означает, что игнорируются индивидуальные свойства элементов группы и происхождение алгебраической операции.

5.Понятие подгруппы.

Непустое подмножество 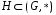называется подгруппой, если 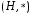само является группой. Более подробно это означает, что 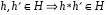, 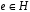и .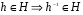

Признак подгруппы.

Непустое подмножество 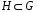будет подгруппой тогда и только тогда, когда .

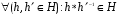Доказательство.

В одну сторону это утверждение очевидно. Пусть теперь 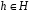- любой элемент. Возьмем 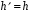в признаке подгруппы. Тогда получим 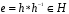. Теперь возьмем 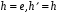. Тогда получим .

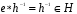Примеры подгрупп.

24.
Для групп преобразований новое и старое понятие подгруппы равносильны между собой.

25.
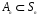- подгруппа четных подстановок.

26.

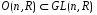
27.
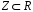и т.д.

28.
Пусть G - любая группа и 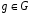- любой фиксированный элемент. Рассмотрим множество 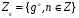всевозможных степеней этого элемента. Поскольку 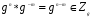, рассматриваемое множество является подгруппой. Она называется циклической подгруппой с образующим элементом g .

29.
Пусть 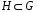любая подгруппа Рассмотрим множество 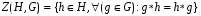- централизатор подгруппы H в группе G. Из определения вытекает, что если 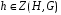, то 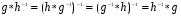, то есть 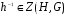. Теперь ясно, что если 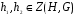, то и 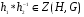и значит централизатор является подгруппой. Если группа G коммутативна, то 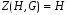. Если G=H, то централизатор состоит из тех элементов, которые перестановочны со всеми элементами группы; в этом случае он называется центром группы G и обозначается Z(G).

Замечание об аддитивной форме записи группы.

Иногда, особенно когда операция в группе коммутативна, она обозначается (+) и называется сложением. В этом случае нейтральный элемент называется нулем и удовлетворяет условию: g+0=g. Обратный элемент в этом случае называется противоположным и обозначается (-g). Степени элемента g имеют вид g+g+...+g , называются кратными элемента g и обозначаются ng.

6. Реализация абстрактной группы как группы преобразований.

Существует несколько способов связать с данной абстрактной группой некоторую группу преобразований. В дальнейшем, если не оговорено противное, знак алгебраической операции в абстрактной группе будет опускаться.

Пусть 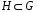некоторая подгруппа.

А) Для каждого 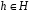определим отображение 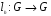(левый сдвиг на элемент h) формулой .

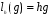Теорема 1

30.

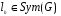
31.
Множество L(H,G)= 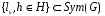является группой преобразований множества G.

32.
Соответствие: 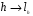является изоморфизмом групп H и L(H,G).

Доказательство.

33.
Надо проверить, что отображение 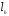взаимно однозначно для всякого 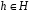. Если 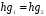, то 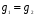по закону сокращения. Значит 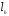инъективно. Если 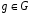любой элемент, то 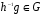и 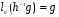так что 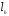к тому же и сюръективно.

34.
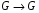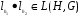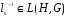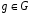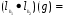
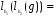
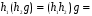
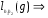
Обозначим через операцию композиции в группе Sym(G) взаимно однозначных отображений . Надо проверить, что и . Пусть любой элемент. Имеем: 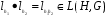; 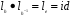и значит, .

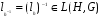35.
Пусть 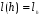. Надо проверить, что l взаимно однозначно и сохраняет операцию. По построению l сюръективно. Инъективность вытекает из закона правого сокращения: 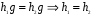. Сохранение операции фактически уже было установлено выше: .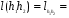

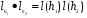Следствие.

Любая абстрактная группа изоморфна группе преобразований некоторого множества (Достаточно взять G=H и рассмотреть левые сдвиги).

Для случая конечных групп получается теорема Кэли:

Любая группа из n элементов изоморфна подгруппе группы 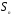подстановок степени n.

36.
Для каждого 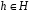определим отображение 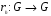(правый сдвиг на элемент h) формулой .

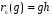Теорема B.

37.
.

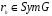38.
Множество 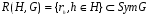является группой преобразований множества G.

39.
Соответствие 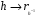является изоморфизмом групп H и R(H,G).

Доказательство теоремы B вполне аналогично доказательству теоремы A. Отметим только, что 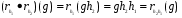. Именно поэтому в пункте 3 теоремы В появляется не 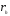, а .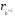

С) Для каждого 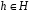определим 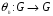(сопряжение или трансформация элементом h ) формулой .

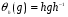Теорема С.

40.
Каждое отображение 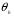является изоморфизмом группы G с собой (автоморфизмом группы G).

41.
Множество 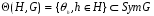является группой преобразований множества G.

42.
Отображение 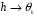сюръективно и сохраняет операцию.

Доказательство.

43.
Поскольку 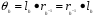, отображение 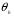взаимно однозначно как композиция двух отображений такого типа. Имеем: 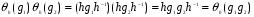и потому 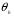сохраняет операцию.

44.
Надо проверить, что 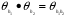и 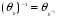. Оба равенства проверяются без труда.

45.
Сюръективность отображения 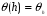имеет место по определению. Сохранение операции уже было проверено в пункте 2.

Замечание об инъективности отображения .

В общем случае отображение не является инъективным. Например, если группа H коммутативна, все преобразования 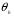будут тождественными и группа 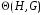тривиальна. Равенство 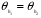означает, что 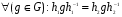или 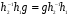(1) В связи с этим удобно ввести следующее определение: множество 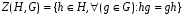называется централизатором подгруппы 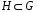. Легко проверить, что централизатор является подгруппой H. Равенство (1) означает, что 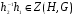. Отсюда вытекает, что если централизатор подгруппы H в G тривиален, отображение является изоморфизмом.

46.
Смежные классы; классы сопряженных элементов.

Пусть, как и выше, 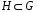некоторая подгруппа. Реализуем H как группу L(H,G) левых сдвигов на группе G. Орбита 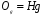называется левым смежным классомгруппы G по подгруппе H. Аналогично, рассматривая правые сдвиги, приходим к правым смежным классам 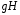.Заметим, что 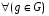стабилизатор St(g, L(H,G)) (как и St(g, R(H,G)) ) тривиален поскольку состоит из таких элементов 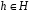, что hg=g 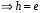. Поэтому, если группа H конечна, то все левые и все правые смежные классы состоят из одинакового числа элементов, равного .

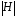Орбиты группы 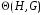называются классами сопряженных элементов группы G относительно подгруппы H и обозначаются 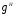Если G=H, говорят просто о классах сопряженных элементов группы G. Классы сопряженных элементов могут состоять из разного числа элементов . Это число равно 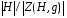, где Z(H,g) подгруппа H , состоящая из всех элементов h перестановочных с g.

Пример.

Пусть 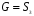- группа подстановок степени 3. Занумеруем ее элементы: 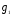=(1,2,3); 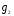=(1,3,2); 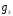=(2,1,3); 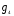=(2,3,1); 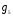=(3,1,2); 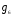=(3,2,1). Пусть 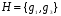. Легко проверить, что левые смежные классы суть:

, , .

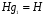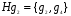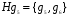Правые смежные классы:

, , .

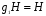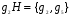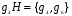Все эти классы состоят из 2 элементов.

Классы сопряженных элементов G относительно подгруппы H:

, , , .

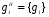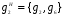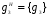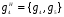В то же время,

, , .

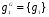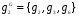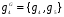Теорема Лагранжа.

Пусть H подгруппа конечной группы G. Тогда порядок H является делителем порядка G.

Доказательство.

По свойству орбит G представляется в виде объединения непересекающихся смежных классов: 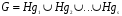. Поскольку все смежные классы состоят из одинакового числа элементов, 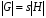, откуда и вытекает теорема.

Замечание. Число s левых (или правых) смежных классов называется индексом подгруппы .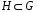

Следствие.

Две конечные подгруппы группы G порядки которых взаимно просты пересекаются только по нейтральному элементу.

В самом деле, если 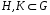эти подгруппы, то 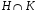их общая подгруппа и по теореме Лагранжа 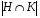- общий делитель порядков H и K то есть 1.

47.
Нормальные подгруппы. Факторгруппы.

Пусть 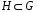любая подгруппа и 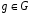-любой элемент. Тогда 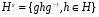также является подгруппой G притом изоморфной H, поскольку отображение сопряжения 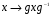является изоморфизмом. Подгруппа 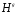называется сопряженной по отношению к подгруппе H.

Определение.

Подгруппа H называется инвариантной или нормальной в группе G, если все сопряженные подгруппы совпадают с ней самой: .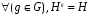

Равенство 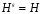можно записать в виде Hg = gH и таким образом, подгруппа инвариантна в том и только в том случае, когда левые и правые смежные классы по этой подгруппе совпадают.

Примеры.

48.
В коммутативной группе все подгруппы нормальны, так как отображение сопряжения в такой группе тождественно.

49.
В любой группе G нормальными будут , во первых, тривиальная подгруппа 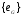и, во вторых, вся группа G. Если других нормальных подгрупп нет, то G называется простой.

50.
В рассмотренной выше группе 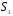подгруппа 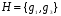не является нормальной так как левые и правые смежные классы не совпадают. Сопряженными с H будут подгруппы 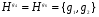и .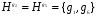

51.
Если 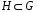- любая подгруппа, то ее централизатор Z = Z(H,G) - нормальная подгруппа в G , так как для всех ее элементов z 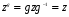. В частности, центр Z(G) любой группы G -нормальная подгруппа.

52.
Подгруппа H индекса 2 нормальна. В самом деле, имеем 2 смежных класса : H и Hg = G-H = gH.

Теорема (свойство смежных классов по нормальной подгруппе).

Если подгруппа H нормальна в G, то множество всевозможных произведений элементов из двух каких либо смежных классов по этой подгруппе снова будет одним из смежных классов, то есть .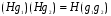

Доказательство.

Очевидно, что для любой подгруппы H 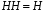.Но тогда

= = = .

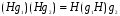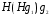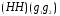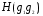Таким образом, в случае нормальной подгруппы H определена алгебраическая операция на множестве смежных классов. Эта операция ассоциативна поскольку происходит из ассоциативного умножения в группе G. Нейтральным элементом для этой операции является смежный класс 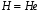. Поскольку 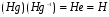, всякий смежный класс имеет обратный. Все это означает, что относительно этой операции множество всех (левых или правых) смежных классов по нормальной подгруппе является группой. Она называется факторгруппой группы G по H и обозначается G/H. Ее порядок равен индексу подгруппы H в G.

26. При́знак дели́мости — алгоритм, позволяющий сравнительно быстро определить, является ли число кратным заранее заданному^[1]. Если признак делимости позволяет выяснить не только делимость числа на заранее заданное, но и остаток от деления, то его называют признаком равноостаточности.

Как правило, признаки делимости применяются при ручном счёте и для чисел, представленных в конкретной позиционной системе счисления (обычно десятичной).

Ризнак делимости на 2

Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2, то есть является чётной.

Признак делимости на 3

Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3 (так как все числа вида 10ⁿ приделении на 3 дают в остатке единицу).

Признак делимости на 4

Число делится на 4 тогда и только тогда, когда число из двух последних его цифр (оно может бытьдвузначным, однозначным или нулём) делится на 4.

Признак делимости на 5

Число делится на 5 тогда и только тогда, когда последняя цифра делится на 5 (то есть равна 0 или 5).

Признак делимости на 6

Число делится на 6 тогда и только тогда, когда оно делится и на 2, и на 3.

Признак делимости на 7

Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этогочисла без последней цифры делится на 7 (например, 364 делится на 7, так как 36 — (2 × 4) = 28 делится на7).

Либо использовать модификацию признака деления на 1001=10³+1, которое само делится на 7:
Для того, чтобы натуральное число делилось на 7 необходимо и достаточно, чтобы алгебраическая суммачисел, образующих нечётные группы по три цифры (начиная с единиц) взятых со знаком «+» и чётных сознаком «-» делилась на семь.

Ещё один признак - берём первую цифру, умножаем на 3, прибавляем следующую (здесь можно взятьостаток от деления на 7 от получившегося числа). И далее - сначала: умножаем на 3, прибавляемследующую... Для 364: 3 * 3 + 6 = 15. Остаток - 1. Далее 1 * 3 + 4 = 7.

Признак делимости на 8

Число делится на 8 тогда и только тогда, когда три его последние цифры — нули или образуют число,которое делится на 8.

Признак делимости на 9

Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.

Признак делимости на 10

Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль.

Признак делимости на 11

Число делится на 11 тогда и только тогда, когда сумма цифр с чередующимися знаками равна 0 или делитсяна 11 (то есть 182 919 делится на 11, так как 1 — 8 + 2 — 9 + 1 — 9 = −22 делится на 11) — следствие факта,что все числа вида 10ⁿ при делении на 11 дают в остатке (-1)ⁿ.

Признак делимости на 12

Число делится на 12 тогда и только тогда, когда оно делится на 3 и на 4.

Признак делимости на 13

Число делится на 13 тогда и только тогда, когда число его десятков, сложенное с учетверённым числомединиц, кратно 13 (например, 845 делится на 13, так как 84 + (4 × 5) = 104 делится на 13).

Признак делимости на 14

Число делится на 14 тогда и только тогда, когда оно делится на 2 и на 7.

Признак делимости на 15

Число делится на 15 тогда и только тогда, когда оно делится на 3 и на 5.

Признак делимости на 17

Число делится на 17 тогда и только тогда, когда число его десятков, сложенное с увеличенным в 12 разчислом единиц, кратно 17 (например, 29053→2905+36=2941→294+12=306→30+72=102→10+24=34.Поскольку 34 делится на 17, то и 29053 делится на 17). Признак не всегда удобен, но имеет определенноезначение в математике. Есть способ немного проще — число делится на 17 тогда и только тогда, когдаразность между числом его десятков и упятерённым числом единиц кратна 17 (например, 32952→3295-10=3285→328-25=303→30-15=15; поскольку 15 не делится на 17, то и 32952 не делится на 17)

Признак делимости на 19

Число делится на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц,кратно 19 (например, 646 делится на 19, так как 64 + (6 × 2) = 76 делится на 19).

Признак делимости на 23

Число делится на 23 тогда и только тогда, когда число его сотен, сложенное с утроенным числом десятков иединиц, кратно 23 (например, 28842 делится на 23, так как 288 + (3 * 42) = 414; продолжаем: 4 + (3 * 14) =46 — очевидно, делится на 23).

Признак делимости на 25

Число делится на 25 тогда и только тогда, когда две его последние цифры делятся на 25 (то есть образуют00, 25, 50 или 75).

Признак делимости на 99

Разобьем число на группы по 2 цифры справа налево (в самой левой группе может быть одна цифра) инайдем сумму этих групп, считая их двузначными числами. Эта сумма делится на 99 тогда и только тогда,когда само число делится на 99.

Признак делимости на 101

Разобьем число на группы по 2 цифры справа налево (в самой левой группе может быть одна цифра) инайдем сумму этих групп с переменными знаками, считая их двузначными числами. Эта сумма делится на101 тогда и только тогда, когда само число делится на 101. Например, 590547 делится на 101, так как 59-05+47=101 делится на 101).

Признак делимости на 2ⁿ

Число делится на n-ю степень двойки тогда и только тогда, когда число, образованное его последними nцифрами, делится на ту же степень.

Признак делимости на 5ⁿ

Число делится на n-ю степень пятёрки тогда и только тогда, когда число, образованное его последними nцифрами, делится на ту же степень.

Признак делимости на 10ⁿ − 1

Разобьем число на группы по n цифр справа налево (в самой левой группе может быть от 1 до n цифр) инайдем сумму этих групп, считая их n-значными числами. Эта сумма делится на 10ⁿ − 1 тогда и только тогда,когда само число делится на 10ⁿ − 1.

Признак делимости на 10ⁿ

Число делится на n-ю степень десятки тогда и только тогда, когда n его последних цифр — нули.

Признак делимости на 10ⁿ + 1

Разобьем число на группы по n цифр справа налево (в самой левой группе может быть от 1 до n цифр) инайдем сумму этих групп с переменными знаками, считая их n-числами. Эта сумма делится на 10ⁿ + 1 тогдаи только тогда, когда само число делится на 10ⁿ + 1.