Правило Лопиталя. Применение к вычислению пределов
Рассмотрим 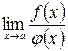 . Если
. Если 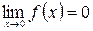 ,
, 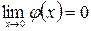 , функции
, функции 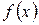 и
и 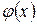 удовлетворяют условиям теоремы Коши и
удовлетворяют условиям теоремы Коши и 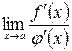 существует, то
существует, то 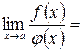
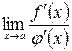 (4.1.)
(4.1.)
Формула (4.1) справедлива и в случае , если 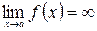 и
и 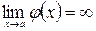 . Правило Лопиталя позволяет раскрывать неопределенности вида
. Правило Лопиталя позволяет раскрывать неопределенности вида 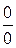 и
и 
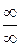 .
.
Пример 4.1. 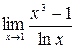
Подстановка предельного значения 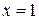 приводит к неопределенности вида
приводит к неопределенности вида 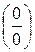 , т.к.
, т.к. 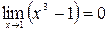 и
и 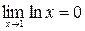 ,
,
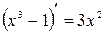 ,
, 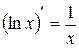 и
и 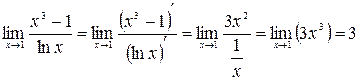 .
.
Пример 4.2. 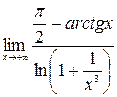 .
.
Напомним, что 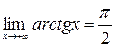 , т.е. имеем неопределенность вида
, т.е. имеем неопределенность вида 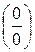 . Находим предел с помощью формулы (4.1):
. Находим предел с помощью формулы (4.1):
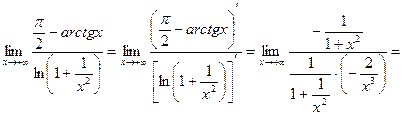
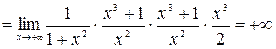 .
.
Пример 4.3. 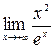 . Здесь числитель и знаменатель одновременно стремятся к бесконечности, т.е. имеем неопределенность вида
. Здесь числитель и знаменатель одновременно стремятся к бесконечности, т.е. имеем неопределенность вида 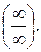 Кроме того,
Кроме того, 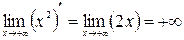 и
и 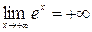 , т.е. необходимо применить правило Лопиталя два раза.
, т.е. необходимо применить правило Лопиталя два раза.
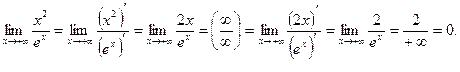
Неопределенности видов 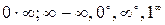 с помощью алгебраических преобразований можно привести к виду
с помощью алгебраических преобразований можно привести к виду 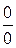
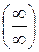 и применить правило Лопиталя.
и применить правило Лопиталя.
Неопределенности вида 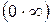 и
и 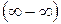 .
.
Если 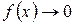 и
и 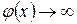 при
при 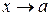 , то отыскание предела
, то отыскание предела 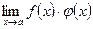 может быть сведено к одному из рассмотренных случаев,
может быть сведено к одному из рассмотренных случаев, 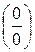 или
или 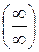 с помощью тождественных преобразований:
с помощью тождественных преобразований: 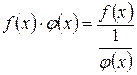 , или
, или 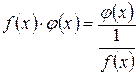 (4.2)
(4.2)
Если 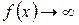 и
и 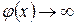 при
при 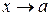 , то отыскание предела
, то отыскание предела 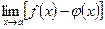 (неопределенность вида
(неопределенность вида 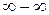 ) может быть сведено к раскрытию неопределенности вида
) может быть сведено к раскрытию неопределенности вида 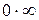 путем тождественного преобразования разности функций в произведение
путем тождественного преобразования разности функций в произведение
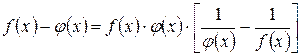 . (4.3)
. (4.3)
Иногда удобно пользоваться и другими преобразованиями:
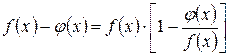 , или
, или 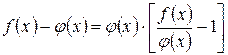 . (4.4)
. (4.4)
Неопределенности вида 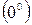 ,
, 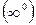 ,
, 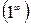 .
.
При отыскании предела функции 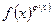 могут представиться случаи:
могут представиться случаи:
1. 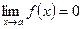 ,
, 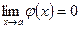 , т.е.
, т.е. 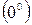 ;
;
2. 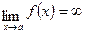 ,
, 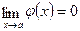 , т.е.
, т.е. 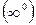 ;
;
3. 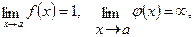 т.е.
т.е. 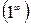 .
.
Вычисление предела функции в этих случаях сводится к раскрытию неопределенности вида 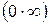 с помощью следующего преобразования:
с помощью следующего преобразования:
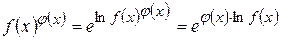 . В силу непрерывности показательной функции, получим
. В силу непрерывности показательной функции, получим
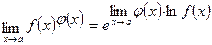 (4.5)
(4.5)
или к раскрытию неопределенностей 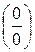 ,
, 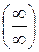 с помощью логарифмирования данной функции.
с помощью логарифмирования данной функции.
Пример 4.4. 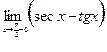 .
.
Если 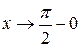 , то
, то 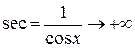 и
и 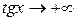 и имеем неопределенность вида
и имеем неопределенность вида 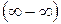 . Преобразуем данную функцию по формуле (4.3)
. Преобразуем данную функцию по формуле (4.3)
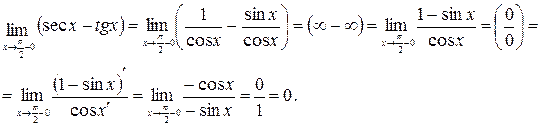
Пример 4.5. 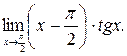 Неопределенность вида
Неопределенность вида 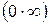 . Преобразуем данную функцию по формуле (4.2)
. Преобразуем данную функцию по формуле (4.2) 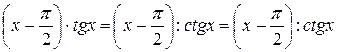 , в результате получим неопределенность вида
, в результате получим неопределенность вида 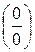 при
при 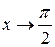 , что дает возможность применить правило Лопиталя.
, что дает возможность применить правило Лопиталя.
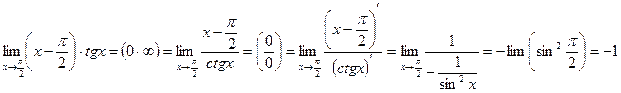
Пример 4.6: 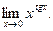 Неопределенность вида
Неопределенность вида 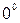 , т.к.
, т.к. 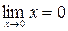 и
и 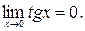 Преобразуем функцию по формуле (4.5) и применим к показателю степени правило Лопиталя:
Преобразуем функцию по формуле (4.5) и применим к показателю степени правило Лопиталя:
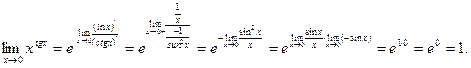
Пример 4.7. 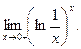 Неопределенность вида
Неопределенность вида 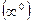 . Преобразуем функцию по формуле (4.5):
. Преобразуем функцию по формуле (4.5): 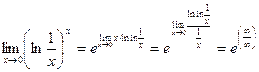 .
.
Заменим переменную, положив 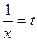 . При
. При 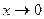 имеем
имеем 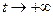 и находим предел в показателе:
и находим предел в показателе:
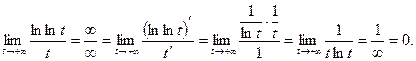
Окончательно, 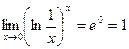 .
.
Пример 4.8. 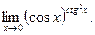 Неопределенность вида
Неопределенность вида 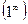 . По формуле (4.5)
. По формуле (4.5)
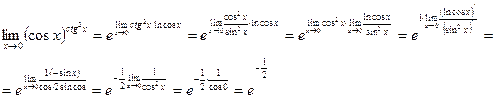
Пример 4.9:
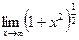 (Неопределенность вида (
(Неопределенность вида ( 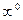 )). Обозначив
)). Обозначив 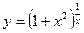 , прологарифмируем функцию и найдем предел логарифма:
, прологарифмируем функцию и найдем предел логарифма:
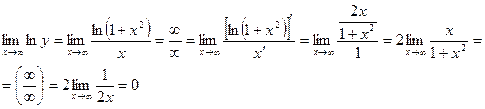
т.е. 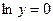 , т.к.
, т.к. 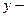 непрерывная функция
непрерывная функция
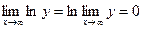 и
и 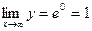 т.е.
т.е. 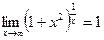 .
.
4.2 Формула Тейлора и её применения.
Пусть функция 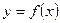 имеет в точке
имеет в точке 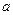 и некоторой её окрестности все производные до
и некоторой её окрестности все производные до 
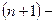 го порядка включительно. Пусть
го порядка включительно. Пусть 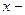 любое значение аргумента из указанной окрестности
любое значение аргумента из указанной окрестности 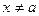 . Тогда между точками
. Тогда между точками 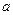 и
и 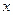 найдется такая точка с, что справедлива следующая формула:
найдется такая точка с, что справедлива следующая формула:
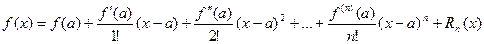 .
.
Эта формула называется формулой Тейлора.
Выражение 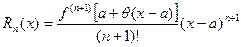 ,
, 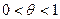 .
.
называется остаточным членом в форме Лагранжа.
Формулой Маклорена называют формулу Тейлора, когда 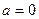 .
.
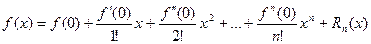 ,
,
где остаточный член, записанный в форме Лагранжа, имеет вид:
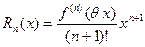 ,
, 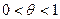 .
.
Разложение некоторых функций по формуле Маклорена
1) 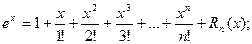
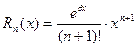 ;
; 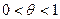 .
.
1. 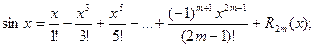
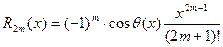 ;
; 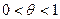 .
.
2. 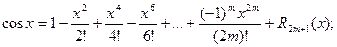
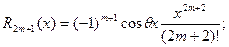
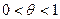 .
.
3. 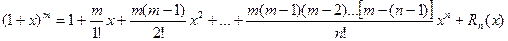 ;
;
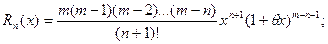
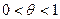 .
.
4. 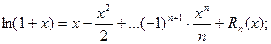
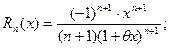
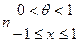 .
.
Приложение формулы Маклорена.
Формула Маклорена дает возможность заменить функцию 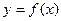 многочленом
многочленом 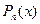 с контролируемой погрешностью, что позволяет использовать ее в приближенных вычислениях.
с контролируемой погрешностью, что позволяет использовать ее в приближенных вычислениях.
Пример 4.10. Найти приближенное значение 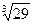 с точностью до
с точностью до 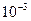 .
.
Решение. Представим заданный корень так: 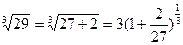 .
.
Воспользуемся биномиальным разложением
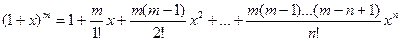
погрешность которого
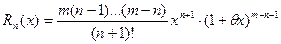
может быть сделана как угодно малой при 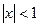 и достаточно большом
и достаточно большом 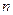 .
.
Пусть 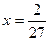 и
и 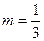 , тогда
, тогда
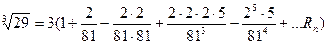 .
.
Оценивая величины последовательных ошибок вычисления 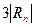 , находим
, находим
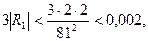
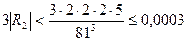 .
.
Следовательно, для вычисления с заданной точностью достаточно взять три члена, которые предшествуют остатку 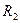 , т.е.
, т.е. 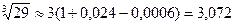 .
.
