Теоремы о свойствах дифференцируемых функций (теорема Ферма, Ролля)

Ответ:

Теорема Ферма

В терминах производных оказывается удобным описывать различные свойства функций. Прежде всего, укажем характеристическое свойство точек, в которых функция принимает наибольшее или наименьшее значение. Напомним, что если функция 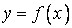определена на некотором множестве X, то говорят, что она принимает в точке x0 наибольшее (наименьшее) значение на множестве X, если для всех точек 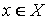выполняется неравенство 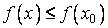(неравенство ).

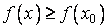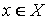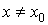Если для всех и выполняется неравенство 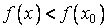(неравенство 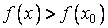), то говорят, что в точке x0 функция 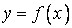принимает строго наибольшее (строго наименьшее) значение на множестве X.

Точки, в которых функция принимает значения (строгого) максимума или минимума, называются точками (строгого) экстремума.

Теорема (теорема Ферма). Пусть функция определена на некотором промежутке и в некоторой внутренней точке этого промежутка принимает наибольшее (наименьшее) значение. Тогда если в этой точке существует конечная производная, то эта производная равна нулю.

Доказательство. Пусть функция 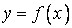определена в окрестности U(x0) точки x0 и принимает для определённости при x = x0 наибольшее значение, т. е. для всех 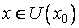выполняется неравенство 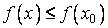. Тогда если x < x0,

,

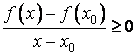а если x > x0, то

.

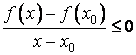По условию теоремы в точке x0 существует конечный предел, поэтому, переходя в неравенствах к пределу при x ® x0, получим соответственно 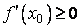и 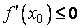. Следовательно, . □

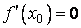Теоремы о среднем.

Теорема Ролля.

(Ролль (1652-1719)- французский математик)

Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то на интервале (а, b) существует точка e, a < e < b, в которой производная функция f(x) равная нулю,

f¢(e) = 0.

Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует точка e такая, что в соответствующей точке кривой y = f(x) касательная параллельна оси Ох. Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки.

Доказательство. По свойству функций, непрерывных на отрезке функция f(x) на отрезке [a, b] принимает наибольшее и наименьшее значения. Обозначим эти значения М и m соответственно. Возможны два различных случая М = m и M ¹ m.

Пусть M = m. Тогда функция f(x) на отрезке [a, b] сохраняет постоянное значение и в любой точке интервала ее производная равна нулю. В этом случае за e можно принять любую точку интервала.

Пусть М = m. Так значения на концах отрезка равны, то хотя бы одно из значений М или m функция принимает внутри отрезка [a, b]. Обозначим e, a < e < b точку, в которой f(e) = M. Так как М- наибольшее значение функции, то для любого Dх ( будем считать, что точка e + Dх находится внутри рассматриваемого интервала) верно неравенство:

Df(e) = f(e + Dx) – f(e) £ 0

При этом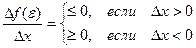

Но так как по условию производная в точке e существует, то существует и предел .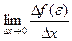

Т.к. 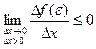и 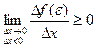, то можно сделать вывод:

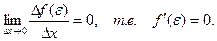
Теорема доказана.

Теорема Ролля имеет несколько следствий:

1) Если функция f(x) на отрезке [a, b] удовлетворяет теореме Ролля, причем

f(a) = f(b) = 0, то существует по крайней мере одна точка e, a < e < b, такая, что f¢(e) = 0. Т.е. между двумя нулями функции найдется хотя бы одна точка, в которой производная функции равна нулю.

2) Если на рассматриваемом интервале (а, b) функция f(x) имеет производную (n-1)- го порядка и n раз обращается в нуль, то существует по крайней мере одна точка интервала, в котором производная (n – 1) – го порядка равна нулю.