ПРИМЕР РЕШЕНИЯ ЗАДАЧИ №1
Ступенчатый брус нагружен силами Р1, Р2, Р3, (Рисунок 2,а).
Требуется построить эпюры продольных сил N, нормальных напряжений s, продольных перемещений D и проверить, выполняется ли условие прочности.
Числовые данные к задаче выбираются по табл. 1.
Например: 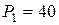 кН,
кН, 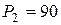 кН,
кН, 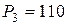 кН,
кН, 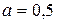 м
м 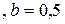 м,
м, 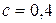 м;
м; 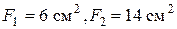 .
.
Для всех вариантов принимается: 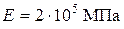 ;
; 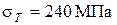
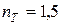 .
.
1. Построение эпюры N.
На брус действуют три силы, следовательно, продольная сила по его длине будет изменяться. Разбиваем брус на участки, в пределах которых продольная сила будет постоянной. В данном случае границами участков являются сечения, в которых приложены силы. Обозначим сечения буквами А, В, С, D, начиная со свободного конца, в данном случае правого.
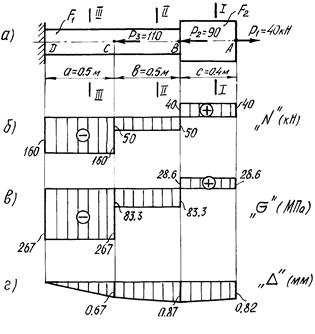 Рисунок 2- Расчетная схема бруса и эпюры: а ‑ расчетная схема; б ‑ эпюра продольных сил; в ‑ эпюра напряжений; г ‑ эпюра продольных перемещений Рисунок 2- Расчетная схема бруса и эпюры: а ‑ расчетная схема; б ‑ эпюра продольных сил; в ‑ эпюра напряжений; г ‑ эпюра продольных перемещений |
Для определения продольной силы на каждом участке рассматриваем произвольное поперечное сечение, сила в котором определяется по правилу, приведенному ранее. Чтобы не определять предварительно реакцию в заделке D, начинаем расчеты со свободного конца бруса А.
Участок АВ, сечение 1-1. Справа от сечения действует растягивающая сила 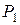 (Рисунок 2, а). В соответствии с упомянутым ранее правилом, получаем
(Рисунок 2, а). В соответствии с упомянутым ранее правилом, получаем
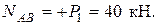
Участок ВС, сечение 2-2. Справа от него расположены две силы, направленные в разные стороны. С учетом правила знаков, получим
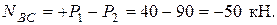
Участок СD, сечение 3-3: аналогично получаем
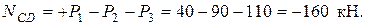
По найденным значениям N в выбранном масштабе строим эпюру, учитывая, что в пределах каждого участка продольная сила постоянна (Рисунок 2 б)
Положительные значения N откладываем вверх от оси эпюры, отрицательные - вниз.
2. Построение эпюры напряжений s.
Вычисляем напряжения в поперечном сечении для каждого участка бруса:
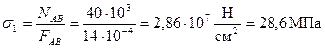 ;
;
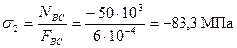 ;
;
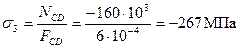 .
.
При вычислении нормальных напряжений значения продольных сил N берутся по эпюре с учетом их знаков. Знак плюс соответствует растяжению, минус - сжатию. Эпюра напряжений показана на Рисунок 2, в.
3. Построение эпюры продольных перемещений.
Для построения эпюры перемещений вычисляем абсолютные удлинения отдельных участков бруса, используя закон Гука:
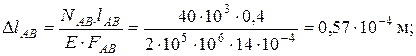
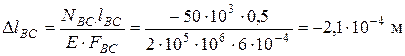 ;
;
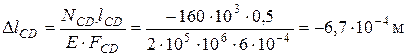 .
.
Определяем перемещения сечений, начиная с неподвижного закрепленного конца. Сечение D расположено в заделке, оно не может смещаться и его перемещение равно нулю:
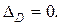
Сечение С переместится в результате изменения длины участка CD. Перемещение сечения С определяется по формуле
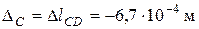 .
.
При отрицательной (сжимающей) силе точка С сместится влево.
Перемещение сечения В является результатом изменения длин DC и CB. Складывая их удлинения, получаем
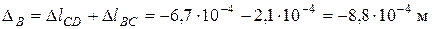 .
.
Рассуждая аналогично, вычисляем перемещение сечения А:
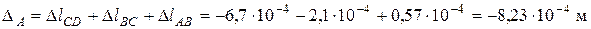 .
.
В выбранном масштабе откладываем от исходной оси значения вычисленных перемещений. Соединив полученные точки прямыми линиями, строим эпюру перемещений (Рисунок 2, г).
4. Проверка прочности бруса.
Условие прочности записывается в следующем виде:
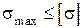 .
.
Максимальное напряжение 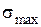 находим по эпюре напряжений, выбирая максимальное по абсолютной величине:
находим по эпюре напряжений, выбирая максимальное по абсолютной величине:
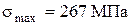 .
.
Это напряжение действует на участке DC, все сечения которого являются опасным.
Допускаемое напряжение вычисляем по формуле:
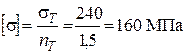 .
.
Сравнивая 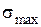 и
и 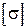 , видим, что условие прочности не выполняется, так как максимальное напряжение превышает допускаемое.
, видим, что условие прочности не выполняется, так как максимальное напряжение превышает допускаемое.
ЗАДАЧА № 2
Абсолютно жесткий брус АВ опирается на шарнирно-неподвижную опору и прикреплен с помощью шарниров к двум стальным стержням.
Требуется подобрать сечения стержней по условию их прочности, приняв запас прочности по отношению к пределу текучести 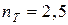 .
.
Соотношение площадей поперечных сечений стержней указано на расчетных схемах, модуль упругости стали для всех вариантов 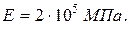
Числовые данные берутся из таблицы 2, расчетные схемы - по рисунку 3.
Таблица 2-Числовые данные к задаче № 2
| Номер строки | Номер расчет. схемы по | Размер, м | Сила, кН | Марка стали | Предел текучести, МПа | ||
| рисунку 3 | а | b | с | ||||
| 1,2 | 1,6 | 1,0 | |||||
| 1,2 | 1,5 | 0,8 | |||||
| 1,4 | 1,4 | 1,0 | |||||
| 1,4 | 1,6 | 0,9 | |||||
| 1,4 | 1,5 | 0,7 | |||||
| 1,3 | 1,4 | 0,8 | |||||
| 1,5 | 1,2 | 1,0 | 40Х | ||||
| 1,5 | 1,1 | 0,9 | |||||
| 1,2 | 1,5 | 1,0 | |||||
| 1.2 | 1.6 | 1,0 | 40Х |
