Параметрическое уравнивание нивелирной сети
Схема нивелирной сети III класса.
Исходные данные:
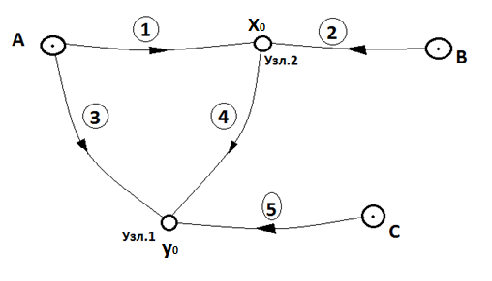
| № ходов | Названия ходов | Н | h | L, км |
| А – Узл 2 | 196,852 | +5,702 | 13,4 | |
| В – Узл 2 | 202,308 | +0,228 | 5,4 | |
| А – Узл 1 | 196,852 | -19,201 | 7,5 | |
| Узл 2 – Узл 1 | -24,895 | 15,6 | ||
| С – Узл 1 | 169,949 | +7,728 | 19,8 |
Обозначим приближенные отметки узловых реперов через xо, yо
Поправки к ним 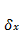 ,
, 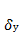
Уравненные отметки x, y
x = xо + 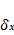
y = yо + 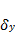
Уравнивание будем выполнять в такой последовательности:
1. От репера А по ходу 3 и от репера В по ходу 2, вычисляем приближенные высоты узловых точек
Xо = Hв + h2 = 202,536
yо = Ha + h3 = 177,651
Составим уравнение поправок, причем начинать надо с точки, на которую указывает стрелка
V1 = xо + 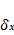 - На – h1 =
- На – h1 = 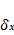 - 1,8(см.)
- 1,8(см.)
V2 = xо + 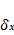 - Нв – h2 =
- Нв – h2 = 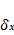 + 0
+ 0
V3 = yо + 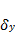 - Нa – h3 =
- Нa – h3 = 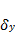 + 0
+ 0
V4 = yо + 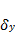 - xо -
- xо - 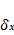 – h4 =
– h4 = 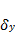 –
– 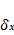 + 1,0 (см.)
+ 1,0 (см.)
V5 = yо + 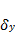 - Нс – h5 =
- Нс – h5 = 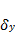 - 2,6 (см.)
- 2,6 (см.)
Составим таблицу коэффициентов уравнений поправок. Так как измерения неравноточные, вычисляем веса ходов.
| № | a | b | l,см | S | P=20/L | V,см | V,мм | PV | P 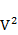 | PlV |
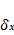 =0,701 =0,701 | 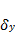 =0,452 =0,452 | |||||||||
| +1 | -1,8 | -0.8 | 1,49 | -1,09 | -10,9 | -1,62 | 1,77 | 2,92 | ||
| +1 | +1 | 3,70 | 0,701 | 7,0 | 2,59 | 1,82 | ||||
| +1 | +1 | 2,67 | 0,452 | 4,5 | 1,21 | 0,55 | ||||
| -1 | +1 | +1,0 | +1 | 1,28 | 0,751 | 7,5 | 0,96 | 0,72 | 0,96 | |
| +1 | -2,6 | -1,6 | 1,01 | -2,148 | -21,5 | -2.17 | 4,66 | 5,64 | ||
| +1 | +3 | -3,4 | 0,6 | 10,15 | 0,97 | 9,52 | 9,52 |
Где S – сумма по строчкам для контроля.
Таблица нормальных уравнений
| a] | b] | l] | s] | Контроль | |
| [Pa | 6,47 | -1,28 | -3,96 | 1,23 | 1,23 = 1,23 |
| [Pb | Учитываем при контроле | 4,96 | -1,35 | 2,33 | 2,33 = 2,33 |
Решение нормальных уравнений.
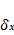 | 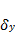 | l | S | Контроль | |
| N1 | 6,47 | -1,28 | -3,96 | +1,23 | |
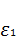 | -1,00 | 0,198 | 0,612 | -0,190 | -0,190 |
| N2 | 4,96 | -1,35 | 2,33 | ||
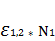 | -0,25 | -0,78 | 0,24 | ||
| N2 | 4,71 | -2,13 | 2,57 | 2,58 | |
 2 2 | -1,00 | 0,452 | -0,546 | -0,548 |
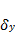 = 0,452
= 0,452
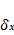 = 0,198*0,452 + 0,612 = 0,701
= 0,198*0,452 + 0,612 = 0,701
Примечание к таблице:
N1 – первое нормальное уравнение
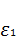 - элиминационное уравнение ( каждый член первого уравнения делим на первый коэффициент с противоположным знаком и получаем
- элиминационное уравнение ( каждый член первого уравнения делим на первый коэффициент с противоположным знаком и получаем 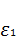 )
)
N2 – второе нормальное уравнение
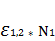 - произведение второго коэффициента элиминационного уравнения на все члены первого нормального уравнения.
- произведение второго коэффициента элиминационного уравнения на все члены первого нормального уравнения.
N2 – преобразованное второе нормальное уравнение ( складываем N2 и
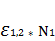 )
)
 2 = второе элиминационное уравнение ( каждый член второго преобразованного уравнения делим на первый коэффициент с противоположным знаком и получаем
2 = второе элиминационное уравнение ( каждый член второго преобразованного уравнения делим на первый коэффициент с противоположным знаком и получаем 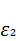 )
)
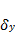 = 0,452
= 0,452
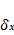 = 0,198*0,452 + 0,612 = 0,701
= 0,198*0,452 + 0,612 = 0,701
Контроль: Полученные значения подставляем в первое уравнение.
6,47*0,701-1,28*0,452 -3,96 = -0,003
Подставляем полученные значения в уравнение поправок и вычисляем поправки в измеренные превышения.
| N | h | V,мм | h испр |
| +5,702 | -11 | +5,691 | |
| +0,228 | +7 | +0,235 | |
| -19,201 | +5 | -19,196 | |
| -24,895 | +8 | -24,887 | |
| +7,728 | -21 | +7,707 |
Контроль:
h3 – h4 – h2 – (Hb – Ha) = 0
h1 + h4 – h5 – (Hc – Ha) = 0
h2 + h4 – h5 – (Hc – Hb) = 0
h1 + h4 – h3 = 0
Вычисление отметок узловых реперов
Узл.1 = 177,651 + 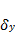 = 177,656
= 177,656
Узл.2 = 202,536 + 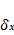 = 202,543
= 202,543
Оценка точности.
Контроль
[P 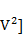 = [PlV] = 9,52
= [PlV] = 9,52
Вычисляем среднюю квадратическую погрешность единицы веса
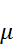 =
= 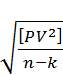 = 17,8 мм
= 17,8 мм
Где n – число ходов (5)
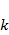 – число узлов (2)
– число узлов (2)
СКО на 1 км. хода
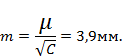
Задача 3
