Условия монотонности функции
Оценка остаточного члена в формуле Тейлора
Неотъемлемой частью использования формулы Тейлора является оценка ее остаточного члена. Красивые и практичные формулы появлялись в работах выдающихся математиков 18, 19 и да в 20 веках. Отметим некоторые результаты без доказательства.
Теорема 1(5). (Теорема Лагранжа) Пусть функция 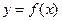 имеет в некоторой окрестности точки
имеет в некоторой окрестности точки 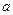 производную
производную 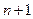 -го порядка. Тогда для произвольной точки
-го порядка. Тогда для произвольной точки 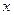 из этой окрестности найдется точка
из этой окрестности найдется точка 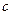 , принадлежащая интервалу, соединяющую точки
, принадлежащая интервалу, соединяющую точки 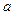 и
и 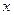 , обладающую тем свойством, что в формуле (5) выполнено соотношение
, обладающую тем свойством, что в формуле (5) выполнено соотношение 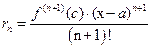 , (13)
, (13)
Теорема 2(6). (Теорема Коши) Пусть функция 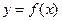 имеет в некоторой окрестности точки
имеет в некоторой окрестности точки 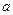 производную
производную 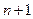 -го порядка. Тогда для произвольной точки
-го порядка. Тогда для произвольной точки 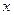 из этой окрестности найдется точка
из этой окрестности найдется точка 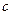 , принадлежащая интервалу, соединяющую точки
, принадлежащая интервалу, соединяющую точки 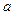 и
и 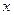 , обладающую тем свойством, что в формуле (5) выполнено соотношение
, обладающую тем свойством, что в формуле (5) выполнено соотношение 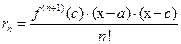 , (14)
, (14)
Теорема 3(5). (Теорема Пеано) Пусть функция 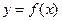 имеет в некоторой окрестности точки
имеет в некоторой окрестности точки 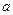 производную
производную 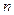 -го порядка. Тогда в формуле (5) выполнено соотношение
-го порядка. Тогда в формуле (5) выполнено соотношение 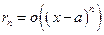 , (15)
, (15)
Так как производные функции 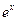 равны между собой и ограничены на любом фиксированном отрезке
равны между собой и ограничены на любом фиксированном отрезке 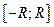 , то остаточный член
, то остаточный член 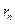 в формуле
в формуле 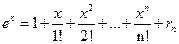 стремится к нулю при
стремится к нулю при 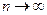 для каждого фиксированного
для каждого фиксированного 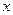 .
.
Тем более то же самое справедливо для функций 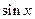 и
и 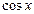 , так как производные этих функций не превосходят по модулю 1. В формулах
, так как производные этих функций не превосходят по модулю 1. В формулах 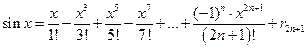 и
и 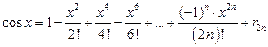 остаточный член стремится к нулю при
остаточный член стремится к нулю при 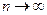 для каждого
для каждого 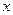 .
.
Можно доказать, что в формуле 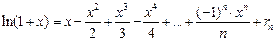 остаточный член стремится к нулю при
остаточный член стремится к нулю при 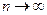 для каждого
для каждого 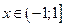 . Посмотрите, как выглядит эта формула при
. Посмотрите, как выглядит эта формула при 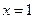 .
.
Условия монотонности функции
Мы приступаем к более сложным вопросам исследования функции 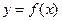 и построения ее графика. Конечно, все начинается определения
и построения ее графика. Конечно, все начинается определения 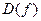 и множества значений
и множества значений 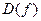 функции
функции 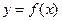 . Также мы уже обсуждали вопросы четности, нечетности и периодичности функции. Теперь мы приступаем к изучению вопросов, связанных в основном с использованием в анализе свойств функции ее производных.
. Также мы уже обсуждали вопросы четности, нечетности и периодичности функции. Теперь мы приступаем к изучению вопросов, связанных в основном с использованием в анализе свойств функции ее производных.
Если большему значению аргумента на множестве соответствует большее значение функции, то такая функция называется, как мы помним, монотонно возрастающей на этом множестве. Аналогично вводятся понятия других монотонных функций: убывающей, неубывающей, невозрастающей.
Как определить монотонность функции на данном промежутке? Мы знаем, что если производная функции положительна в точке, то она возрастает в некоторой окрестности этой точки. Отсюда следует, что если производная функции положительна на интервале, то функция является возрастающей на этом интервале. А как быть с граничными точками отрезка, как быть с теми точками, в которых производная функции равна 0 или не существует?
Теорема 1. Пусть функция 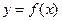 непрерывна на отрезке
непрерывна на отрезке 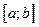 , имеет производную
, имеет производную 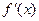 на интервале
на интервале 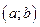 во всех точках, за исключением конечного числа точек, в которых производная равна 0 или не существует. Тогда, если производная положительна во всех точках, где она существует, то функция
во всех точках, за исключением конечного числа точек, в которых производная равна 0 или не существует. Тогда, если производная положительна во всех точках, где она существует, то функция 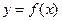 возрастает на отрезке
возрастает на отрезке 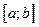 , а если производная отрицательна во всех точках, где она существует, то функция
, а если производная отрицательна во всех точках, где она существует, то функция 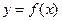 убывает на отрезке
убывает на отрезке 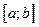 ,
,
Доказательство. Разобьем отрезок 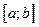 на имеющие не более одной общей точки отрезки, во внутренних точках каждого из которых производная (для определенности) положительна. Следовательно, в силу непрерывности на всем отрезке выполнено условие: большему значению аргумента соответствует большее значение функции. Теорема доказана.
на имеющие не более одной общей точки отрезки, во внутренних точках каждого из которых производная (для определенности) положительна. Следовательно, в силу непрерывности на всем отрезке выполнено условие: большему значению аргумента соответствует большее значение функции. Теорема доказана.
