Дифференциальные уравнения 2-го порядка
§1. Методы понижения порядка уравнения.
Дифференциальное уравнение 2-го порядка имеет вид:
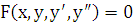 . (1.1)
. (1.1)
Общим решением уравнения является семейство функций, зависящее от двух произвольных постоянных 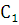 и
и 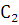 :
: 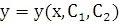 (или
(или 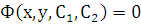 – общий интеграл дифференциального уравнения 2-го порядка). Задача Коши для дифференциального уравнения 2-го порядка (1.1) состоит в отыскании частного решения уравнения, удовлетворяющего начальным условиям: при
– общий интеграл дифференциального уравнения 2-го порядка). Задача Коши для дифференциального уравнения 2-го порядка (1.1) состоит в отыскании частного решения уравнения, удовлетворяющего начальным условиям: при 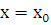 :
: 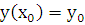 ,
, 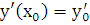 . Необходимо заметить, что графики решений уравнения 2-го порядка могут пересекаться в отличие от графиков решений уравнения 1-го порядка. Однако решение задачи Коши для уравнений 2-го порядка (1.1) при довольно широких предположениях для функций, входящих в уравнение, единственно, т.е. всякие два решения с общим начальным условием
. Необходимо заметить, что графики решений уравнения 2-го порядка могут пересекаться в отличие от графиков решений уравнения 1-го порядка. Однако решение задачи Коши для уравнений 2-го порядка (1.1) при довольно широких предположениях для функций, входящих в уравнение, единственно, т.е. всякие два решения с общим начальным условием 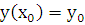 ,
, 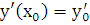 совпадают на пересечении интервалов определения.
совпадают на пересечении интервалов определения.
Получить общее решение или решить задачу Коши для дифференциального уравнения 2-го порядка аналитически удается далеко не всегда. Однако в некоторых случаях удается понизить порядок уравнения с помощью введения различных подстановок. Разберем эти случаи.
1. Уравнения, не содержащие явно независимой переменной 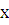 .
.
Пусть дифференциальное уравнение 2-го порядка имеет вид: 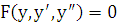 , т.е. в уравнении (1.1) явно не присутствует независимая переменная
, т.е. в уравнении (1.1) явно не присутствует независимая переменная 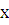 . Это позволяет принять
. Это позволяет принять 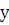 за новый аргумент, а производную 1-го порядка
за новый аргумент, а производную 1-го порядка 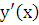 принять за новую функцию
принять за новую функцию 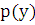 . Тогда
. Тогда 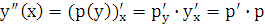 .
.
Таким образом, уравнение 2-го порядка 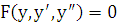 для функции
для функции 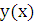 , не содержащее явно
, не содержащее явно 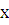 , свелось к уравнению 1-го порядка
, свелось к уравнению 1-го порядка 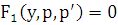 для функции
для функции 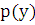 . Интегрируя это уравнение, получаем общий интеграл
. Интегрируя это уравнение, получаем общий интеграл 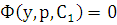 или
или 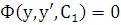 , а это есть дифференциальное уравнение 1-го порядка для функции
, а это есть дифференциальное уравнение 1-го порядка для функции 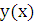 . Решая его, получаем общий интеграл исходного дифференциального уравнения, зависящий от двух произвольных постоянных:
. Решая его, получаем общий интеграл исходного дифференциального уравнения, зависящий от двух произвольных постоянных: 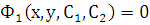 .
.
Пример 1. Решить дифференциальное уравнение 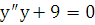 при заданных начальных условиях:
при заданных начальных условиях: 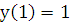 ,
, 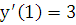 .
.
Решение.
Так как в исходном уравнении в явном виде отсутствует аргумент 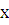 , то примем
, то примем 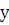 за новую независимую переменную, а
за новую независимую переменную, а 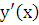 – за
– за 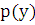 . Тогда
. Тогда 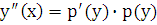 и уравнение приобретает следующий вид для функции
и уравнение приобретает следующий вид для функции 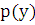 :
: 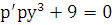 .
.
Это дифференциальное уравнение с разделяющимися переменными: 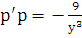 . Откуда следует
. Откуда следует 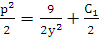 , т.е.
, т.е. 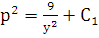 .
.
Так как при 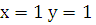 и
и 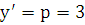 , то подставляя начальные условия в последнее равенство, получаем, что
, то подставляя начальные условия в последнее равенство, получаем, что 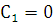 и
и 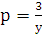 , что равносильно
, что равносильно 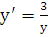 . В результате для функции
. В результате для функции 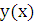 имеем уравнение с разделяющимися переменными, решая которое, получаем
имеем уравнение с разделяющимися переменными, решая которое, получаем 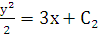 . Используя начальные условия, получаем, что
. Используя начальные условия, получаем, что 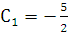 . Следовательно, частный интеграл уравнения, удовлетворяющий начальным условиям, имеет вид:
. Следовательно, частный интеграл уравнения, удовлетворяющий начальным условиям, имеет вид: 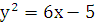 .
.
2. Уравнения, не содержащие явно искомой функции 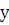 .
.
Пусть дифференциальное уравнение 2-го порядка имеет вид: 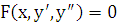 , т.е. в уравнение явно не входит искомая функция
, т.е. в уравнение явно не входит искомая функция 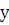 . В этом случае вводят постановку
. В этом случае вводят постановку 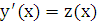 . Тогда
. Тогда 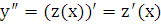 и уравнение 2-го порядка
и уравнение 2-го порядка 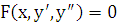 для функции
для функции 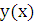 переходит в уравнение 1-го порядка
переходит в уравнение 1-го порядка 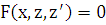 для функции
для функции 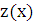 . Проинтегрировав его, получаем дифференциальное уравнение 1-го порядка для функции
. Проинтегрировав его, получаем дифференциальное уравнение 1-го порядка для функции 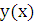 :
: 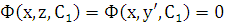 . Решая последнее уравнение, получаем общий интеграл заданного дифференциального уравнения
. Решая последнее уравнение, получаем общий интеграл заданного дифференциального уравнения 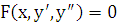 , зависящий от двух произвольных постоянных:
, зависящий от двух произвольных постоянных: 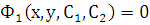 .
.
Пример 2. Найти общее решение уравнения: 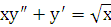
Решение.
В данное уравнение 2-го порядка явно не входит искомая функция 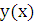 , следовательно, делаем замену:
, следовательно, делаем замену: 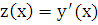 и
и 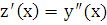 . В результате чего получаем дифференциальное уравнение 1-го порядка для функции
. В результате чего получаем дифференциальное уравнение 1-го порядка для функции 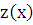 :
: 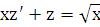 или
или 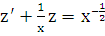 , являющееся линейным уравнением. Решая его, получаем:
, являющееся линейным уравнением. Решая его, получаем: 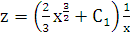 или
или 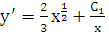 . Итак, для функции
. Итак, для функции 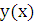 получили дифференциальное уравнение с разделяющимися переменными:
получили дифференциальное уравнение с разделяющимися переменными: 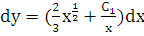 , откуда следует общее решение исходного уравнения:
, откуда следует общее решение исходного уравнения: 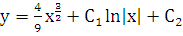 .
.
3. Порядок степени понижается, если удается преобразовать его к такому виду, что обе части уравнения становятся полными производными по 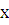 от каких-нибудь функций. Например, пусть дано уравнение
от каких-нибудь функций. Например, пусть дано уравнение 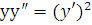 . Деля обе части на
. Деля обе части на 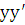 , получаем
, получаем 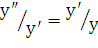 ;
; 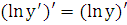 ;
; 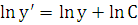 ;
; 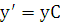 – порядок уравнения понижен.
– порядок уравнения понижен.
§2. Линейное дифференциальное уравнение 2-го порядка.
Линейное дифференциальное уравнение (ЛДУ) 2-го порядка имеет следующий вид:
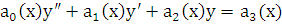 , (2.1)
, (2.1)
где 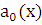 ,
, 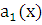 ,
, 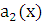 и
и 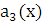 – заданные функции, непрерывные на том промежутке, на котором ищется решение. Предполагая, что a0(x) ≠ 0, поделим (2.1) на
– заданные функции, непрерывные на том промежутке, на котором ищется решение. Предполагая, что a0(x) ≠ 0, поделим (2.1) на 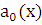 и, после введения новых обозначений для коэффициентов, запишем уравнение в виде:
и, после введения новых обозначений для коэффициентов, запишем уравнение в виде:
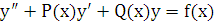 (2.2)
(2.2)
Примем без доказательства, что (2.2) имеет на некотором промежутке единственное решение, удовлетворяющее любым начальным условиям 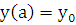 ,
, 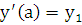 , если на рассматриваемом промежутке функции
, если на рассматриваемом промежутке функции 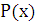 ,
, 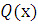 и
и 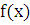 непрерывны. Если
непрерывны. Если 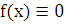 , то уравнение (2.2) называется однородным, и уравнение (2.2) называется неоднородным в противном случае.
, то уравнение (2.2) называется однородным, и уравнение (2.2) называется неоднородным в противном случае.
Рассмотрим свойства решений лоду 2-го порядка.
Определение. Линейной комбинацией функций 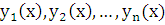 называется выражение
называется выражение 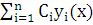 , где
, где 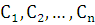 – произвольные числа.
– произвольные числа.
Теорема. Если 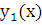 и
и 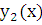 – решение лоду
– решение лоду
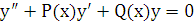 , (2.3)
, (2.3)
то их линейная комбинация 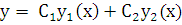 также будет решением этого уравнения.
также будет решением этого уравнения.
Доказательство.
Поставим выражение 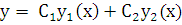 в (2.3) и покажем, что в результате получается тождество:
в (2.3) и покажем, что в результате получается тождество:
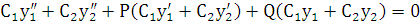 .
.
Перегруппируем слагаемые:
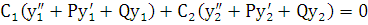 .
.
Поскольку функции 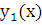 и
и 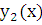 являются решениями уравнения (2.3), то каждая из скобок в последнем уравнении тождественно равна нулю, что и требовалось доказать.
являются решениями уравнения (2.3), то каждая из скобок в последнем уравнении тождественно равна нулю, что и требовалось доказать.
Следствие 1. Из доказанной теоремы вытекает при 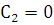 , что если
, что если 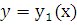 – решение уравнения (2.3), то
– решение уравнения (2.3), то 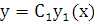 тоже есть решение этого уравнения.
тоже есть решение этого уравнения.
Следствие 2. Полагая 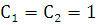 , видим, что сумма двух решений лоду
, видим, что сумма двух решений лоду 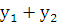 также является решением этого уравнения.
также является решением этого уравнения.
Замечание. Доказанное в теореме свойство решений остается справедливым для лоду любого порядка.
§3. Определитель Вронского.
Определение. Система функций 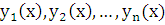 называется линейно независимой на некотором промежутке, если ни одна из этих функций не представляется в виде линейной комбинации всех остальных.
называется линейно независимой на некотором промежутке, если ни одна из этих функций не представляется в виде линейной комбинации всех остальных.
В случае двух функций 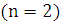 это означает, что
это означает, что 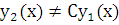 , т.е.
, т.е. 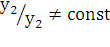 . Последнее условие можно переписать в виде
. Последнее условие можно переписать в виде 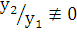 или
или 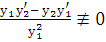 . Стоящий в числителе этого выражения определитель
. Стоящий в числителе этого выражения определитель 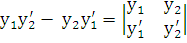 называется определителем Вронского для функций
называется определителем Вронского для функций 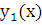 и
и 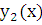 . Таким образом, определитель Вронского для двух линейно независимых функций не может быть тождественно равен нулю.
. Таким образом, определитель Вронского для двух линейно независимых функций не может быть тождественно равен нулю.
Пусть 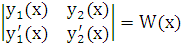 – определитель Вронского для линейно независимых решений
– определитель Вронского для линейно независимых решений 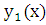 и
и 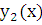 уравнения (2.3). Убедимся подстановкой, что функция
уравнения (2.3). Убедимся подстановкой, что функция 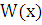 удовлетворяет уравнению
удовлетворяет уравнению 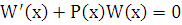 . (3.1)
. (3.1)
Действительно, 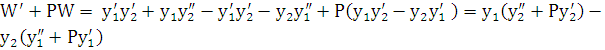 . Поскольку функции
. Поскольку функции 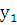 и
и 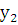 удовлетворяют уравнению (2.3), то
удовлетворяют уравнению (2.3), то 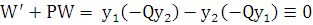 , т.е.
, т.е. 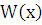 – решение уравнения (3.1). Найдем это решение:
– решение уравнения (3.1). Найдем это решение: 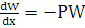 ;
; 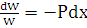 . Откуда
. Откуда 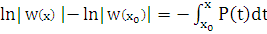 ,
, 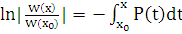 .
. 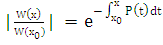 ,
, 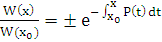 ,
, 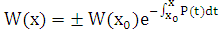 .
.
В правой части этой формулы надо взять знак плюс, так как только в этом случае при 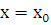 получается тождество. Таким образом,
получается тождество. Таким образом,
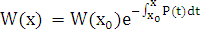 (3.2)
(3.2)
Это формула называется формулой Лиувилля. Выше было показано, что определитель Вронского для линейно независимых функций не может быть тождественно равен нулю. Следовательно, существует такая точка 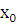 , в которой определитель для линейно независимых решений уравнения (2.3)
, в которой определитель для линейно независимых решений уравнения (2.3) 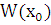 отличен от нуля. Тогда из формулы Лиувилля следует, что функция
отличен от нуля. Тогда из формулы Лиувилля следует, что функция 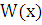 будет отлична от нуля при всех значениях
будет отлична от нуля при всех значениях 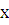 из рассматриваемого промежутка, поскольку при любом значении
из рассматриваемого промежутка, поскольку при любом значении 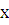 оба множителя в правой части формулы (3.2) отличны от нуля.
оба множителя в правой части формулы (3.2) отличны от нуля.
§4. Структура общего решения лоду 2-го порядка.
Теорема. Если 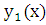 и
и 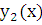 – линейно независимые решения уравнения (2.3), то их линейная комбинация
– линейно независимые решения уравнения (2.3), то их линейная комбинация 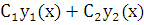 , где
, где 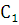 и
и 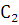 – произвольные постоянные, будет общим решением этого уравнения.
– произвольные постоянные, будет общим решением этого уравнения.
Доказательство.
То, что 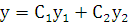 есть решение уравнения (2.3), следует из теоремы о свойствах решений лоду 2-го порядка. Надо только еще показать, что решение
есть решение уравнения (2.3), следует из теоремы о свойствах решений лоду 2-го порядка. Надо только еще показать, что решение 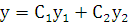 будет общим, т.е. надо показать, что при любых начальных условиях
будет общим, т.е. надо показать, что при любых начальных условиях 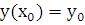 ,
, 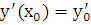 можно выбрать произвольные постоянные
можно выбрать произвольные постоянные 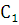 и
и 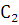 так, чтобы удовлетворить этим условиям. Запишем начальные условия в виде:
так, чтобы удовлетворить этим условиям. Запишем начальные условия в виде:
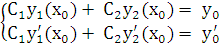
Постоянные 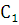 и
и 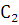 из этой системы линейных алгебраических уравнений определяются однозначно, так как определитель этой системы
из этой системы линейных алгебраических уравнений определяются однозначно, так как определитель этой системы 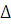 есть значение определителя Вронского для линейно независимых решений лоду при
есть значение определителя Вронского для линейно независимых решений лоду при 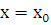 :
:
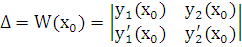 ,
,
а такой определитель, как мы видели в предыдущем параграфе, отличен от нуля. Теорема доказана.
Пример. Доказать, что функция 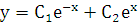 , где
, где 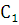 и
и 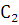 – произвольные постоянные, является общим решением лоду
– произвольные постоянные, является общим решением лоду 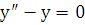 .
.
Решение.
Легко убедиться подстановкой, что функции 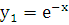 и
и 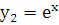 удовлетворяют данному уравнению. Эти функции являются линейно независимыми, так как
удовлетворяют данному уравнению. Эти функции являются линейно независимыми, так как 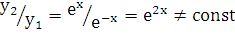 . Поэтому согласно теореме о структуре общего решения лоду 2-го порядка
. Поэтому согласно теореме о структуре общего решения лоду 2-го порядка 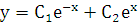 является общим решением данного уравнения.
является общим решением данного уравнения.
§5. ЛОДУ 2-го порядка с постоянными коэффициентами.
Дано лоду 2-го порядка с постоянными коэффициентами 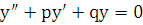 (5.1), где
(5.1), где 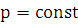 ,
, 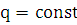 . Согласно предыдущему параграфу общее решение лоду 2-го порядка легко определяется, если известны два линейно независимых частных решения этого уравнения. Простой метод нахождения частных решений уравнения с постоянными коэффициентами предложил Л. Эйлер. Это метод, который называется методом Эйлера, состоит в том, что частные решения ищутся в виде
. Согласно предыдущему параграфу общее решение лоду 2-го порядка легко определяется, если известны два линейно независимых частных решения этого уравнения. Простой метод нахождения частных решений уравнения с постоянными коэффициентами предложил Л. Эйлер. Это метод, который называется методом Эйлера, состоит в том, что частные решения ищутся в виде 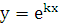 .
.
Подставляя эту функцию в уравнение (5.1), после сокращения на 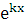 , получим алгебраическое уравнение, которое называется характеристическим:
, получим алгебраическое уравнение, которое называется характеристическим:
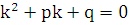 (5.2)
(5.2)
Функция 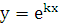 будет решением уравнения (5.1) только при тех значениях k, которые являются корнями характеристического уравнения (5.2). В зависимости от величины дискриминанта
будет решением уравнения (5.1) только при тех значениях k, которые являются корнями характеристического уравнения (5.2). В зависимости от величины дискриминанта 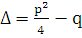 возможны три случая.
возможны три случая.
1. 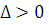 . Тогда корни характеристического уравнения различны:
. Тогда корни характеристического уравнения различны: 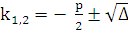 . Решения
. Решения 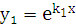 и
и 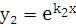 будут линейно независимыми, т.к.
будут линейно независимыми, т.к. 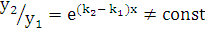 и общее решение (5.1) можно записать в виде
и общее решение (5.1) можно записать в виде 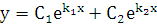 .
.
2. 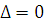 . В этом случае
. В этом случае 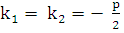 и
и 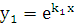 . В качестве второго линейно независимого решения
. В качестве второго линейно независимого решения 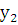 можно взять функцию
можно взять функцию 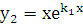 . Проверим, что эта функция удовлетворяет уравнению (5.1). Действительно,
. Проверим, что эта функция удовлетворяет уравнению (5.1). Действительно, 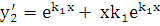 ,
, 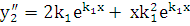 . Подставляя эти выражения в уравнение (5.1), получим
. Подставляя эти выражения в уравнение (5.1), получим
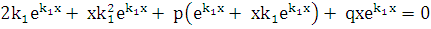 или
или 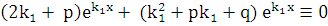 , т.к.
, т.к. 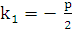 и
и 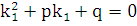 .
.
Частные решения 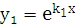 и
и 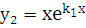 линейно независимы, т.к.
линейно независимы, т.к. 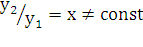 . Следовательно, общее решение (5.1) имеет вид:
. Следовательно, общее решение (5.1) имеет вид:
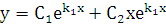 или
или 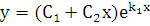 .
.
3. 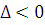 . В этом случае корни характеристического уравнения комплексно-сопряженные:
. В этом случае корни характеристического уравнения комплексно-сопряженные: 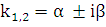 , где
, где 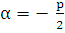 ,
, 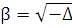 . Можно проверить, что линейно независимыми решениями уравнения (5.1) будут функции
. Можно проверить, что линейно независимыми решениями уравнения (5.1) будут функции 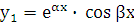 и
и 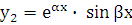 . Убедимся, что уравнению (5.1) удовлетворяет, например, функция y1. Действительно,
. Убедимся, что уравнению (5.1) удовлетворяет, например, функция y1. Действительно, 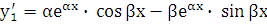 ,
, 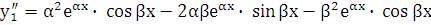 . Подставив эти выражения в уравнение (5.1), получим
. Подставив эти выражения в уравнение (5.1), получим
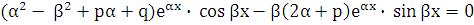 .
.
Обе скобки в левой части этого равенства тождественно равны нулю. Действительно, 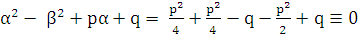 ,
,
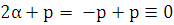 . Таким образом, функция
. Таким образом, функция 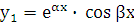 удовлетворяет уравнению (5.1). Аналогично нетрудно убедиться в том, что и
удовлетворяет уравнению (5.1). Аналогично нетрудно убедиться в том, что и 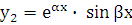 есть решение уравнения (5.1). Поскольку
есть решение уравнения (5.1). Поскольку 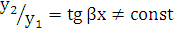 , то общее решение
, то общее решение 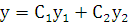 будет иметь вид:
будет иметь вид:
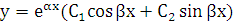 .
.
§6. Структура общего решения линейного неоднородного дифференциального уравнения (лнду) 2-го порядка.
Теорема 1. Общее решение лнду 2-го порядка
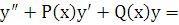 f(x) (6.1)
f(x) (6.1)
представляется в виде суммы общего решения 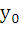 соответствующего однородного уравнения
соответствующего однородного уравнения
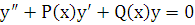 (6.2)
(6.2)
и любого частного решения 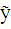 лнду (6.1).
лнду (6.1).
Доказательство.
Докажем сначала, что 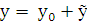 будет решением уравнения (6.1). Для этого подставим
будет решением уравнения (6.1). Для этого подставим 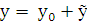 в уравнение (6.1):
в уравнение (6.1): 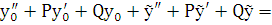 f(x). Это равенство является тождеством, т.к.
f(x). Это равенство является тождеством, т.к. 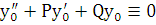 и
и 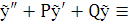 f(x). Следовательно,
f(x). Следовательно, 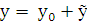 есть решение уравнения (6.1).
есть решение уравнения (6.1).
Докажем теперь, что это решение является общим, т.е. можно так выбрать входящие в него произвольные постоянные, что будут удовлетворяться любые начальные условия вида: 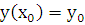 ,
, 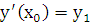 (6.3). Согласно теореме о структуре общего решения линейного однородного дифференциального уравнения (лоду) общее решение уравнения (6.2) можно представить в виде
(6.3). Согласно теореме о структуре общего решения линейного однородного дифференциального уравнения (лоду) общее решение уравнения (6.2) можно представить в виде 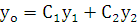 , где
, где 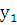 и
и 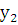 – линейно независимые решения этого уравнения. Таким образом:
– линейно независимые решения этого уравнения. Таким образом:
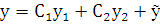 и, следовательно, начальные условия (6.3) можно записать в виде:
и, следовательно, начальные условия (6.3) можно записать в виде:
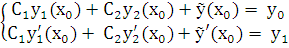
или
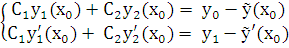 (6.4)
(6.4)
Произвольные постоянные 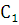 и
и 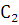 определяются из этой системы линейных алгебраических уравнений однозначно при любых правых частях, т.к. определитель этой системы
определяются из этой системы линейных алгебраических уравнений однозначно при любых правых частях, т.к. определитель этой системы 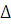 =
= 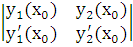 есть значение определителя Вронского для линейно независимых решений уравнения (6.2) при
есть значение определителя Вронского для линейно независимых решений уравнения (6.2) при 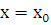 , а такой определитель, как мы видели выше, отличен от нуля. Определив постоянные
, а такой определитель, как мы видели выше, отличен от нуля. Определив постоянные 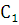 и
и 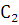 из системы уравнений (6.4) и подставив их в выражение
из системы уравнений (6.4) и подставив их в выражение 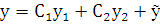 , мы получим частное решение уравнения (6.1), удовлетворяющее заданным начальным условиям. Теорема доказана.
, мы получим частное решение уравнения (6.1), удовлетворяющее заданным начальным условиям. Теорема доказана.
Докажем еще одну простую теорему, которая часто используется при решении лнду.
Теорема 2. Если 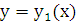 - решение дифференциального уравнения
- решение дифференциального уравнения 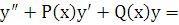 f1(x), а
f1(x), а 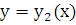 - решение уравнения
- решение уравнения 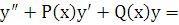 f2(x), то функция
f2(x), то функция 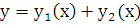 будет решением уравнения
будет решением уравнения
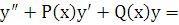 f1(x) + f2(x). (6.5)
f1(x) + f2(x). (6.5)
Доказательство.
Подставив функцию 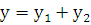 в уравнение (6.5), получим
в уравнение (6.5), получим
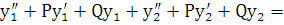 f1 + f2. Это равенство является тождеством, т.к.
f1 + f2. Это равенство является тождеством, т.к. 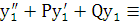 f1 и
f1 и 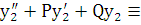 f2. Теорема доказана.
f2. Теорема доказана.
§7. Решение лнду 2-го порядка с постоянными коэффициентами со специальной правой частью.
Пусть в уравнении (6.1) коэффициенты постоянны, т.е. уравнение имеет вид:
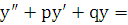 f(x) (7.1)
f(x) (7.1)
где 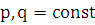 .
.
Рассмотрим метод отыскания частного решения 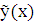 уравнения (7.1) в случае, когда правая часть f(x) имеет специальный вид. Это метод называется методом неопределенных коэффициентов и состоит в подборе частного решения в зависимости от вида правой части f(x). Рассмотрим правые части следующего вида:
уравнения (7.1) в случае, когда правая часть f(x) имеет специальный вид. Это метод называется методом неопределенных коэффициентов и состоит в подборе частного решения в зависимости от вида правой части f(x). Рассмотрим правые части следующего вида:
1. f(x) 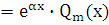 , где
, где 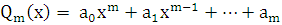 – многочлен степени
– многочлен степени 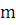 , причем некоторые коэффициенты, кроме
, причем некоторые коэффициенты, кроме 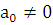 , могут равняться нулю. Укажем вид, в котором надо брать частное решение в этом случае.
, могут равняться нулю. Укажем вид, в котором надо брать частное решение в этом случае.
а) Если число 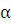 не является корнем характеристического уравнения для уравнения (5.1), то частное решение записываем в виде:
не является корнем характеристического уравнения для уравнения (5.1), то частное решение записываем в виде: 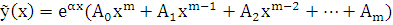 , где
, где 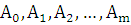 – неопределенные коэффициенты, которые подлежат определению методом неопределенных коэффициентов.
– неопределенные коэффициенты, которые подлежат определению методом неопределенных коэффициентов.
Пример 1. Найти общее решение уравнения 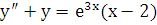 .
.
Решение.
Для уравнения 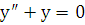 составляем характеристическое уравнение:
составляем характеристическое уравнение: 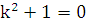 . Откуда получаем
. Откуда получаем 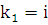 ,
, 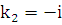 . Следовательно, общее решение однородного уравнения есть
. Следовательно, общее решение однородного уравнения есть 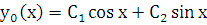 . Правая часть заданного уравнения f(x)
. Правая часть заданного уравнения f(x) 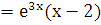 имеет специальный вид (случай 1), причем
имеет специальный вид (случай 1), причем 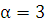 не является корнем характеристического уравнения, поэтому частное решение ищем в виде:
не является корнем характеристического уравнения, поэтому частное решение ищем в виде: 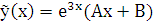 , где
, где 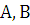 – неопределенные коэффициенты. Найдем производные первого и второго порядков и подставим их в заданное уравнение:
– неопределенные коэффициенты. Найдем производные первого и второго порядков и подставим их в заданное уравнение:
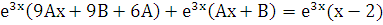 .
.
Обе части сокращаем на 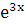 и приравниваем коэффициенты при одинаковых степенях
и приравниваем коэффициенты при одинаковых степенях 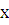 в левой и правой частях равенства
в левой и правой частях равенства
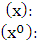
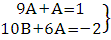
Из полученной системы уравнений находим: 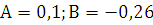 . Тогда
. Тогда 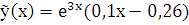 , а общее решение заданного уравнения есть:
, а общее решение заданного уравнения есть:
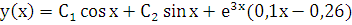 .
.
б) Если 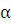 является корнем кратности
является корнем кратности 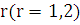 соответствующего характеристического уравнения, то частное решение ищем в виде:
соответствующего характеристического уравнения, то частное решение ищем в виде:
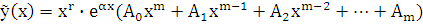 ,
,
где 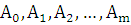 – неопределенные коэффициенты.
– неопределенные коэффициенты.
Пример 2. Решить уравнение 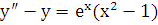 .
.
Решение.
Соответствующее характеристическое уравнение имеет вид:
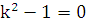 , откуда
, откуда 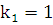 ,
, 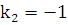 . Тогда общее решение однородного уравнения
. Тогда общее решение однородного уравнения 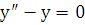 есть:
есть: 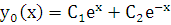 .
.
Правая часть заданного уравнения имеет специальный вид (случай 1). Так как 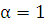 является корнем характеристического уравнения кратности
является корнем характеристического уравнения кратности 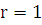 , то частное решение ищется в виде:
, то частное решение ищется в виде:
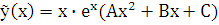 . Находим неопределенные коэффициенты
. Находим неопределенные коэффициенты 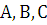 методом, изложенным в примере 1. В результате получаем
методом, изложенным в примере 1. В результате получаем 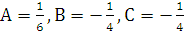 . Окончательно имеем следующее выражение для общего решения:
. Окончательно имеем следующее выражение для общего решения:
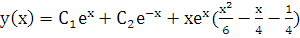 .
.
2. Правая часть f(x) 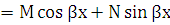 , где хотя бы одно из чисел
, где хотя бы одно из чисел 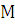 и
и 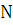 отлично от нуля. Укажем вид частного решения в этом случае.
отлично от нуля. Укажем вид частного решения в этом случае.
а) Если число 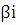 не является корнем характеристического уравнения для уравнения (5.1), то частное решение ищем в виде:
не является корнем характеристического уравнения для уравнения (5.1), то частное решение ищем в виде:
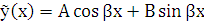 ,
,
где 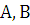 – неопределенные коэффициенты.
– неопределенные коэффициенты.
б) Если число 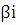 является корнем характеристического уравнения для уравнения (5.1), причем его кратность
является корнем характеристического уравнения для уравнения (5.1), причем его кратность 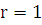 , то записываем частное решение в виде:
, то записываем частное решение в виде:
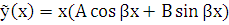 ,
,
где 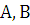 – неопределенные коэффициенты.
– неопределенные коэффициенты.
Пример 3. Решить уравнение 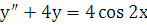 .
.
Решение.
Корни характеристического уравнения для уравнения 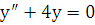 будут
будут 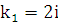 ,
, 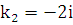 . Тогда общее решение этого лоду:
. Тогда общее решение этого лоду: 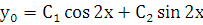 .
.
Правая часть заданного в примере 3 уравнения имеет специальный вид: f(x) 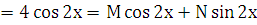 , где
, где 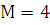 , а
, а 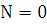 . Число
. Число 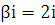 является корнем характеристического уравнения кратности
является корнем характеристического уравнения кратности 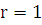 , поэтому частное решение лнду имеет вид:
, поэтому частное решение лнду имеет вид: 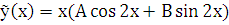 .
.
Для определения 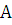 и
и 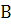 находим
находим 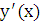 ,
, 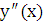 и подставляем в заданное уравнение:
и подставляем в заданное уравнение:
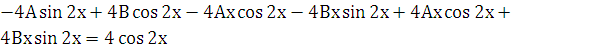 .
.
Приводя подобные члены, приравнивая коэффициенты при 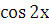 ,
, 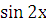 , получаем следующую систему:
, получаем следующую систему: 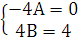 , отсюда
, отсюда 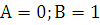 .
.
Окончательно общее решение заданного уравнения имеет вид: 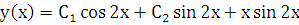 .
.
3. f(x) 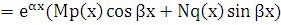 , где
, где 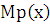 и
и 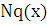 - многочлены степени
- многочлены степени 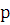 и
и 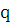 соответственно, причем один из этих многочленов может равняться нулю. Укажем вид частного решения в этом общем случае.
соответственно, причем один из этих многочленов может равняться нулю. Укажем вид частного решения в этом общем случае.
а) Если число 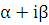 не является корнем характеристического уравнения для уравнения (5.1), то вид частного решения будет:
не является корнем характеристического уравнения для уравнения (5.1), то вид частного решения будет:
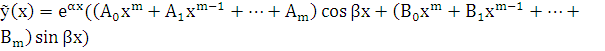 , (7.2)
, (7.2)
где 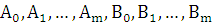 – неопределенные коэффициенты, а
– неопределенные коэффициенты, а 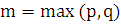 .
.
б) Если число 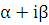 является корнем характеристического уравнения для уравнения (5.1) кратности
является корнем характеристического уравнения для уравнения (5.1) кратности 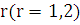 , то частное решение лнду будет иметь вид:
, то частное решение лнду будет иметь вид:
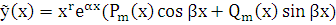 , (7.3)
, (7.3)
т.е. частное решение вида (7.2) надо умножить на 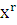 . В выражении (7.3)
. В выражении (7.3) 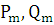 - многочлены с неопределенными коэффициентами, причем их степень
- многочлены с неопределенными коэффициентами, причем их степень 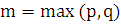 .
.
Пример 4. Указать вид частного решения для уравнения
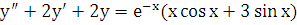 .
.
Решение.
Характеристическое уравнение имеет вид: 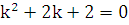 . Его корни:
. Его корни: 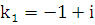 ,
, 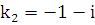 . Общее решение лоду имеет вид:
. Общее решение лоду имеет вид:
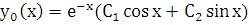 .
.
Правая часть заданного уравнения имеет специальный вид (случай 3): f(x) 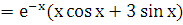 . Число
. Число 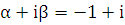 является корнем характеристического уравнения кратности
является корнем характеристического уравнения кратности 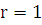 . Коэффициент при
. Коэффициент при 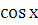 есть многочлен первой степени, а при
есть многочлен первой степени, а при 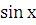 - нулевой степени, поэтому степень многочленов с неопределенными коэффициентами надо брать
- нулевой степени, поэтому степень многочленов с неопределенными коэффициентами надо брать 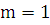 . Итак, вид частного решения:
. Итак, вид частного решения:
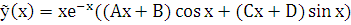 .
.
Далее коэффициенты 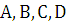 могут быть определены по методу неопределенных коэффициентов.
могут быть определены по методу неопределенных коэффициентов.
