Вычисление ранга матрицы с помощью элементарных преобразований

Элементарными называются следующие преобразования матрицы:

1) перестановка двух любых строк (или столбцов),

2) умножение строки (или столбца) на отличное от нуля число,

3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.

Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.

Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.

Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например,

.

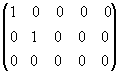При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.

Пример 2 Найти ранг матрицы

А=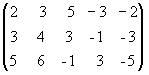

и привести ее к каноническому виду.

Решение. Из второй строки вычтем первую и переставим эти строки:

.

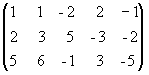Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:

;

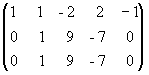из третьей строки вычтем первую; получим матрицу

В = ,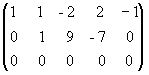

которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:

.

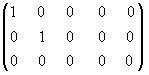№19

Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Для того чтобы линейная система являлась совместной, необходимо и достаточно, что бы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы.

Доказательство (условия совместности системы)

Необходимость

Пусть система совместна. Тогда существуют числа 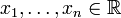такие, что 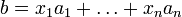. Следовательно, столбец 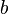является линейной комбинацией столбцов 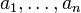матрицы 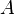. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что .

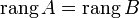Достаточность

Пусть 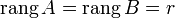. Возьмем в матрице 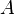какой-нибудь базисный минор. Так как 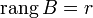, то он же и будет базисным минором и матрицы 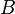. Тогда, согласно теореме о базисном миноре, последний столбец матрицы 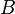будет линейной комбинацией базисных столбцов, то есть столбцов матрицы 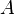. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы .

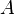Следствия

· Количество главных переменных системы равно рангу системы.

· Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

№20