ПРИМЕР РЕШЕНИЯ ЗАДАЧИ №2

Жесткий брус АВ закреплен, как показано на Рисунок4, и нагружен силой 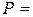5 кН.

Требуется подобрать сечения сте­ржней из условия их прочности. Числовые данные к задаче берутся из табл.2. Для данной задачи примем

а =1,2 м; в =1,4 м; с =1,0 м материал - сталь 40,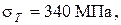

.

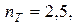
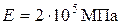Вычислим степень статической неопределимости.

Жесткий брус АВ закреплен с помощью шарнирно-неподвиж­ной опоры и поддерживается двумя деформируемыми стальными стержнями АЕ и ВК. На опоре С (Рисунок 4) - две составляющие реакции X_C и Y_C , реакции в стержнях направлены вдоль их осей и приложены к брусу АВ в точках А и В. Направление этих реакций рекомендуется установить после анализа возможного деформированного состояния конструкции.

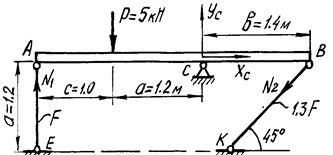Рисунок 4 - Расчетная схема

Для плоской системы сил в общем случае ее приложения к конструкции можно составить только три независимых уравнения равновесия. В рас­смат­риваемой задаче к брусу АВ приложено четыре неизвестных усилия: две реак­ции в шарнире и два усилия в стержнях. Разность между числом неизвестных уси­лий и числом уравнений статики показывает, что для определения этих не­известных необходимо составить еще одно уравнение ста­тики, в которое вхо­дили бы интересующие нас величины. Такое ура­в­не­ние или несколько подоб­ных уравнений можно получить из геометрических зависимостей между деформациями элементов задан­ной конструкции.

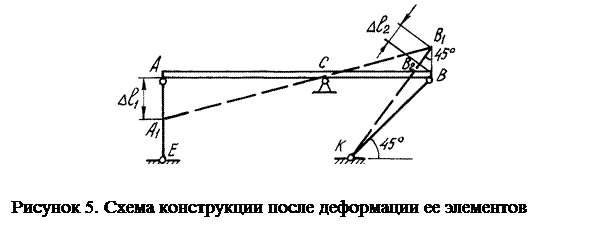
Рассмотрим конструкцию после деформации ее элементов (Рисунок5). Под действием силы Р жесткий брус может повернуться вокруг точки С, при этом стержни АЕ и ВК будут деформированы. Точки А и В описывают при пово­роте бруса ду­ги окружностей, которые ввиду малости перемещений заме­няются каса­тельными, т.е. считается, что эти точки перемещаются по перпен­дикулярам к радиусам АС и ВС этих дуг. Точка А смещается вниз и занимает по­ло­­жение , точка В - вверх, занимая положение . Брус, как абсолютно же­ст­кий элемент конструкции, - положение .Очевидно, что стержень АЕ сжат и стал короче на величину 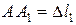. Соединив точки К и 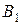, находим на чертеже положение стержня ВК после его деформации. Опустив перпен­ди­куляр из точки В на прямую 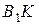, находим точку .

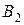Отрезок 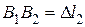- удли­нение стержня ВК.

Действительно, 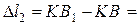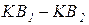, так как КВ=КВ₂, и стер­жень КВ растянут.

Выяснив направление усилий в стержнях, показываем векторы этих усилий на схеме недеформированного состояния конструкции (см. Рисунок 4) и составляем уравнение ее равновесия:

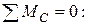
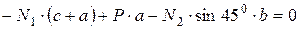(2.1)

Определения составляющих реакции шарнира 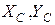для решения данной задачи не требуется, и два других уравнения статики не составля­ются.

Для вычисления усилий в стержнях 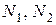необходимо иметь еще одно уравнение, называемое уравнением совместности деформаций. Это уравне­ние получаем из геометрических соотношений между деформациями эле­мен­тов заданной конструкции. При этом ввиду малости деформаций изменением угла наклона стержня ВК пре­небрегаем, считая что Ð .

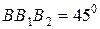Тогда

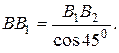
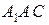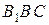Из подобия треугольников и находим соотношение между деформациями стержней - :

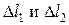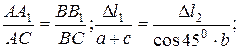
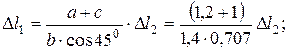
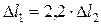(2.2)

Полученная зависимость (2.2) называется условием совместности деформаций.

Абсолютные удлинения стержней можно выразить через усилия, используя формулу Гука (1.2):

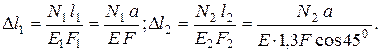(2.3)

Подставив выражения (2.3) в условие совместности деформаций (2.2), получим

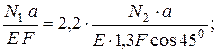
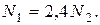(2.4)

Решая систему уравнений (2.1) и (2.4), определяем усилия в стержнях 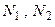. Для этого подставим значение N₁ из (2.4) в уравнение (2.2):

;

.

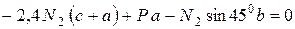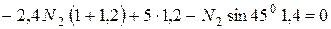Решив систему уравнений, получим

.

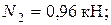
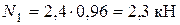Определив усилия в стержнях, переходим к подбору площадей их поперечных сечений.

Для заданного материала по формуле (1.13) вычислим допускаемое на­пряжение

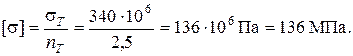
Определяем напряжения в стержнях и выбираем большее:

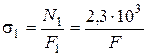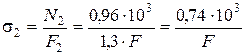Па ;

Па.

Площадь сечения F подбираем по условию прочности наиболее на­гру­жен­ного стержня. Так как 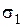больше 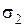, используем условие проч­ности первого сте­р­жня:

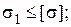
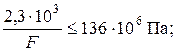
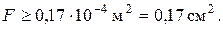
Площади сечений стержней принимаем в соответствии с заданным со­от­ношением:

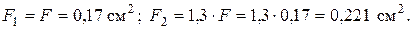
Определение допускаемой силы Р по условию задачи производится по предельной грузоподъемности конструкции.

Предельным состоянием конструкции называется такое состояние, при ко­то­ром она начинает деформироваться без увеличения нагрузки.

В данном примере это произойдет в том случае, когда напряжения во всех стерж­нях достигнут предела текучести

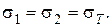
Усилия в стержнях будут определяться по формулам

(2.5)

Нагрузка, соответствующая предельному состоянию, называется предельной. Ее величину можно найти из уравнения предельного равновесия, которое по­лучается из уравнения (2.1) после подстановки в него значений :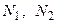

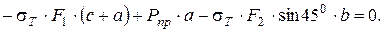
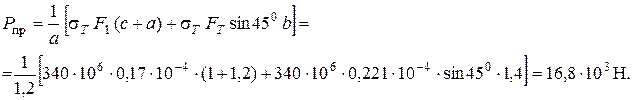
Допускаемая нагрузка с учетом заданного коэффициента запаса

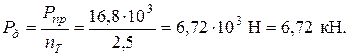
Величина допускаемой нагрузки при расчете по предельной грузо­подъ­ем­ности получается большей, чем при расчете по допускаемым напряжениям:

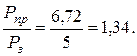
Разница составляет 34 %, что является результатом разных предположений об опасном состоянии конструкции: при расчете по допускаемым напряжениям опасным считается состояние, при котором только в одном стержне напряжение дос­ти­га­ет предела текучести. Для статически неопределимых систем расчет по пре­дель­ной грузоподъемности дает более экономичное решение при назначении размеров сечения, и им широко пользуются в строительной практике.

ЗАДАЧА № 3

Для двух заданных сечений, состоящих из нескольких элементов или име­ю­щих вырезы, определить положение главных центральных осей инер­ции и вы­чис­лить величины моментов инерции относительно этих осей.

Первое сечение для расчета выбирается по рисунку 5, второе - по рисунку 6. Размеры элементов сечений и номера прокатных профилей берутся из таблицы 3. При рас­чете сечения, состоящего из прокатных профилей, уголок следует при­нимать в соответствии с заданными размерами; он может быть равнобоким или не­рав­нобоким.