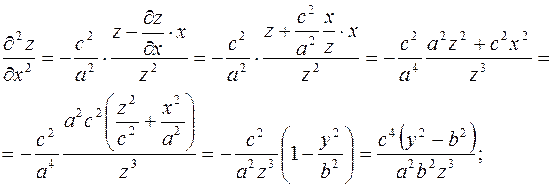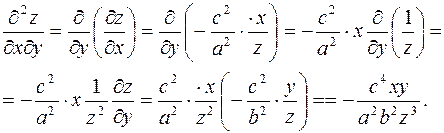Дифференцирование функции

Дифференцирование суммы, произведения, частного функции нескольких переменных производится по обычным правилам дифференцирования.

7.1. Полный дифференциал сложной функции

Если у функции 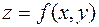каждая переменная в свою очередь является функцией одной или нескольких независимых переменных, то полный дифференциал этой сложной функции вычисляется по той же формуле, что и для функции независимых переменных

.

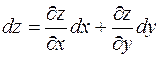В этом проявляется инвариантность формы первого дифференциала.

7.2. Дифференциал высшего порядка функции нескольких независимых переменных.

Пусть функция 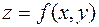имеет вторые непрерывные частные производные. Второй дифференциал от нее определяется равенством

,

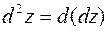при этом дифференциалы dx, dy рассматриваются как независящие от, x y и дифференциал 2-го порядка функции z вычисляется по формуле .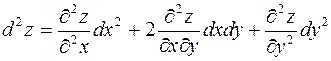

Для функции большего числа переменных 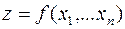с использованием сокращенного обозначения символа суммирования получим следующую формулу

.

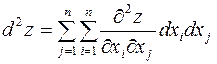Так как 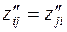, то второй дифференциал от нее представляет собой квадратичную форму относительно независимых дифференциалов 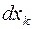: k=1,…,n. Отметим, квадратичной формой от переменных 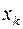: k=1,…,n называется функция вида

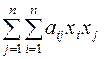, где .

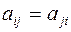Для дифференциала n-го порядка функции двух независимых переменных 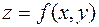при наличии соответствующих производных справедлива следующая символическая формула:

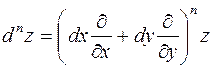, которая формально развертывается по биномиальному закону. Вообще, дифференциал произвольного порядка от функции z для независимых дифференциалов 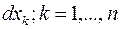определяется по индукции при помощи рекуррентного соотношения

,

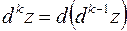где 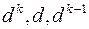берутся для независимых дифференциалов 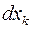, которые к тому же рассматриваются при вычислениях как постоянные. В многомерном случае имеет место аналогичная символическая формула

.

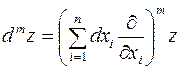7.3. Дифференциал высшего порядка функции нескольких

зависимых переменных

Если 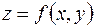, где аргументы есть функции одного переменного или нескольких зависимых переменных, то при наличии соответствующих производных для дифференциала 2-го порядка справедлива формула

.

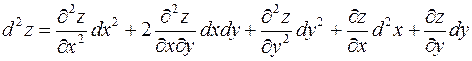Если 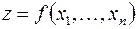, то этой формуле можно придать следующую символическую форму:

.

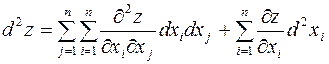Вычисление дифференциалов более высших порядков через зависимые переменные 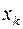производится подобным образом последовательно, учитывая рекуррентное соотношение

,

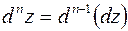основные правила дифференцирования и зависимость производных от аргументов.

7.4. Производная сложной функции одной независимой переменной

Если 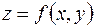есть дифференцируемая функции аргументов 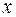и 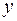, которые в свою очередь являются дифференцируемыми функциями независимой переменной :

,

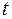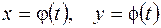то имеет место формула

.

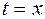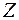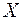В частности, если , то «полная» производная функции по равна

.

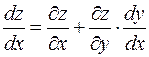Пример. .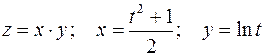

.

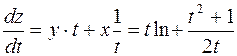Пример. .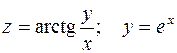

;

.

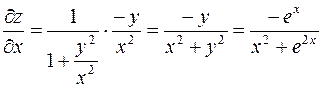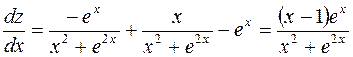7.5. Производная сложной функции нескольких независимых переменных

Если 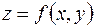, где 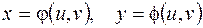есть дифференцируемые функции, 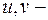независимые переменные, то частные производные выражаются так:

; .

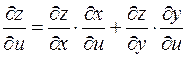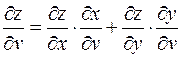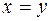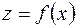В частности, если , то , где 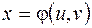и частные производные равны

; .

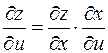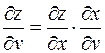Пример.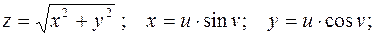

;

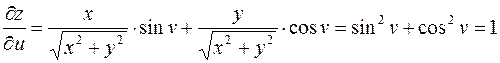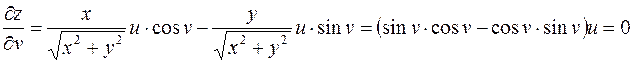
Пример.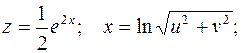

;

.

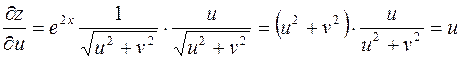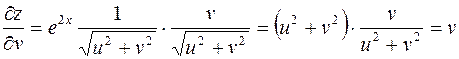7.6. Производная неявной функции

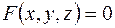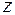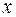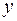Если уравнение определяет как функцию независимых переменных и , где 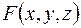- дифференцируемая функция всех своих переменных и 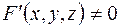, то частные производные этой неявно заданной функции находятся по формулам

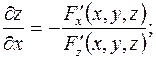
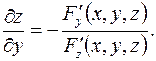
Если 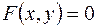, то неявная функция имеет только одну независимую переменную и производная неявно заданной функции равна

.

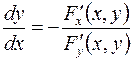Пример.

;

;

.

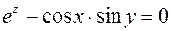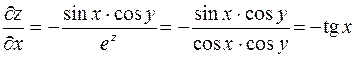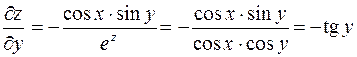Пример.

;

.

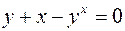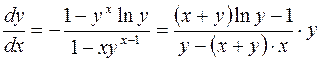7.7. Производная неявных функций, определяемых системой уравнений

Если 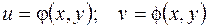есть дифференцируемые функции независимых переменных 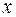и 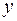, определяемые неявно системой уравнений

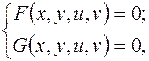
где 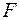и 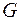- дифференцируемые функции своих переменных и якобиан

,

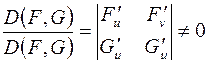то частные производные этих неявных функций находятся из системы уравнений

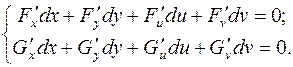
В частности, если 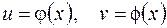, то эта система уравнений принимает следующий вид:

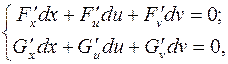
где 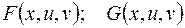- дифференцируемые функции своих переменных и их якобиан не равен нулю.

Пример.

– ?

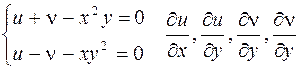Решение.

;

.

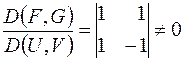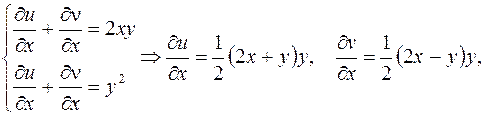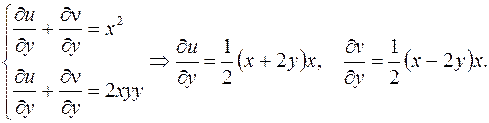
Пример.

?

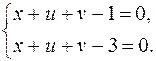
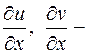Решение.

;

.

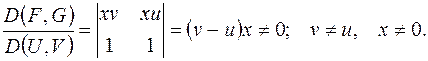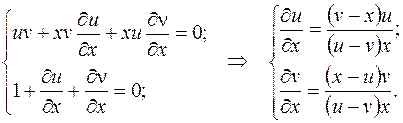7.8. Производная функции, заданной параметрически

Если 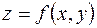есть дифференцируемая функция переменных 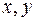, заданная параметрическими уравнениями

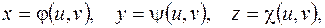
где 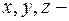дифференцируемые функции своих переменных и якобиан

,

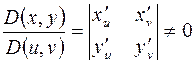то частные производные функции, заданной параметрически, могут быть найдены из системы уравнений

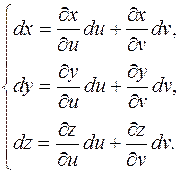
Пример.

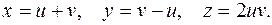
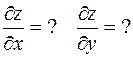
Решение.

.

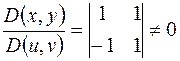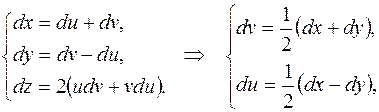
подставляя выражения для 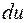и 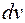в выражение для 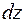, получаем

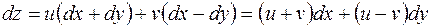
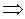
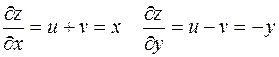
7.9. Производные высших порядков сложных и неявных

функций

Частные производные высших порядков сложных и неявных функций вычисляются дифференцированием формул, определяющих производные, порядок которых ниже на единицу. Скажем, чтобы найти вторую производную от функции 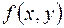, например, 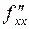, нужно продифференцировать по 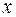частным образом выражение ранее определенной первой производной 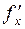, помня при этом, что фигурирующая в нем функция 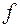зависит от 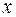, т.е. следует применить правило дифференцирования сложной функции.

В результате выражение для 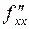может содержать производную 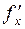. Последнюю следует заменить уже найденным для нее значением.

Пример.

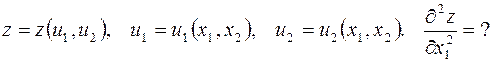
На основании (7.5) запишем:

.

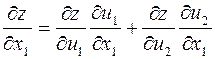Далее:

.

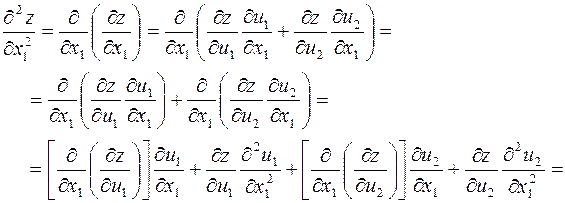
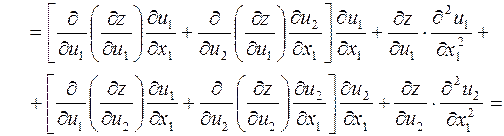
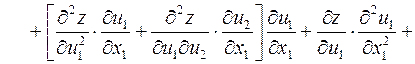
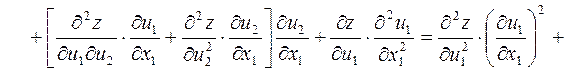
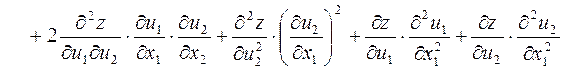Пример.

.

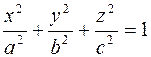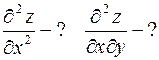
Введем обозначение: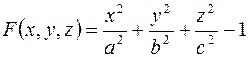

Согласно (7.6) запишем

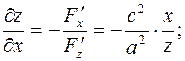
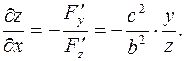
Далее, определим вторые производные: