Наивероятнейшее число успехов
Биномиальное распределение (распределение по схеме Бернулли) позволяет, в частности, установить, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов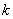 
(появлений события) имеет вид:
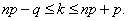
Так как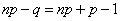 
, то эти границы отличаются на 1. Поэтому 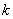, являющееся целым числом, может принимать либо одно значение, когда 
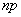целое число ( 
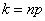) , то есть когда 
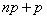(а отсюда и 
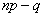) нецелое число, либо два значения, когда 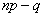целое число.
Пример. При автоматической наводке орудия вероятность попадания по быстро движущейся цели равна 0,9. Найти наивероятнейшее число попаданий при 50 выстрелах.
Решение. Здесь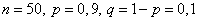 
. Поэтому имеем неравенства:
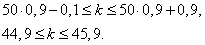
Следовательно,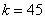 
.
Пример. Данные длительной проверки качества выпускаемых стандартных деталей показали, что в среднем брак составляет 7,5%. Определить наиболее вероятное число вполне исправных деталей в партии из 39 штук.
Решение. Обозначая вероятность выпуска исправной детали через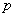 
, будем иметь 
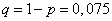и 
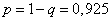(получение бракованной детали и получение исправной детали — события противоположные). Так как здесь n=39, то искомое число можно найти из неравенств:
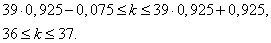
Отсюда наивероятнейшее число исправных деталей равно 36 или 37.
Неравенства для наивероятнейшего числа успехов 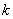позволяют решить и обратную задачу: по данному 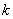и известному значению р определить общее число n всех испытаний.
Пример. При каком числе выстрелов наивероятнейшее число попаданий равно 16, если вероятность попадания в отдельном выстреле составляет 0,7?
Решение. Здесь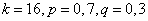 
.
Составляем неравенства
,
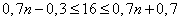откуда
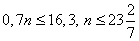и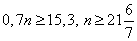 
Таким образом, число всех выстрелов здесь может быть 22 или 23.
Формула Пуассона
При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно, например,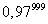 
вычислить трудно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет k раз, используют формулу Пуассона:
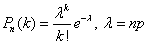– среднее число появлений события в n испытаниях.
Эта формула дает удовлетворительное приближение для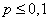 
и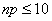 
. При больших 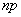рекомендуется применять формулы Лапласа (Муавра-Лапласа). Cобытия, для которых применима формула Пуассона, называют редкими, так как вероятность их осуществления очень мала (обычно порядка 0,001-0,0001).
Пример. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.
Решение. По условию дано: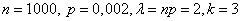 
.
Искомая вероятность
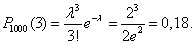
Пример. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути 0,004. Найти вероятность того, что в пути повреждено меньше трех изделий.
Решение. По условию дано: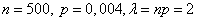 
.
По теореме сложения вероятностей
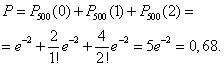
Пример. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит более двух разбитых бутылок.
Решение. По условию дано: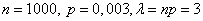 
.
Получаем:
