Базис. Координаты вектора
Перенесем результаты, известные из курса линейной алгебры для алгебраических векторов на частный случай геометрических векторов.
Определение. Любая линейно независимая система трех векторов в трехмерном пространстве называется базисом этого пространства.
В соответствии с критериями линейной зависимости двух и трех векторов можно утверждать, что на плоскости любая пара неколлинеарных векторов, а в пространстве любая тройка некомпланарных векторов образует базис. Обратимся к пространственному случаю.
Теорема. Пусть в трехмерном пространстве система векторов 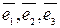 образует базис. Тогда любой вектор
образует базис. Тогда любой вектор 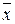 представим в виде некоторой линейной комбинации базисных векторов:
представим в виде некоторой линейной комбинации базисных векторов:
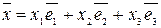 ,
,
где 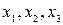 - коэффициенты этой линейной комбинации. При этом такое разложение фиксированного вектора по базисным векторам определено однозначно.
- коэффициенты этой линейной комбинации. При этом такое разложение фиксированного вектора по базисным векторам определено однозначно.
Пусть в векторном пространстве зафиксирован базис 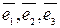 . Тогда любой вектор
. Тогда любой вектор 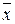 этого векторного пространства в соответствии с последней теоремой можно разложить по данному базису:
этого векторного пространства в соответствии с последней теоремой можно разложить по данному базису:
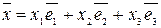
Определение. Коэффициенты 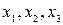 указанного разложения вектора
указанного разложения вектора 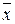 называются координатами этого вектора в данном базисе.
называются координатами этого вектора в данном базисе.
Замечание. В данном векторном пространстве базис может быть определен различным образом. При смене базиса координаты вектора естественно могут меняться.
В соответствии с последней теоремой в данном базисе координаты вектора определены однозначно. Другими словами, каждому вектору 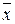 ставится в соответствие единственный упорядоченный набор его координат:
ставится в соответствие единственный упорядоченный набор его координат: 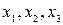 .
.
С другой стороны, если взять упорядоченный набор чисел 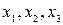 , то в данном базисе он однозначно определяет некоторый вектор
, то в данном базисе он однозначно определяет некоторый вектор
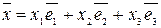 .
.
Таким образом, для фиксированного базиса в данном векторном пространстве можно отождествлять любой вектор с его координатами, т.е. в трехмерном пространстве вектор можно определять как упорядоченный набор трех чисел – его координат. То, что в заданном базисе вектор имеет координаты 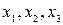 , будем обозначать:
, будем обозначать:
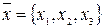 .
.
Теорема.Система трех векторов
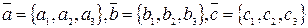
в трехмерном пространстве является базисом тогда и только тогда, когда определитель
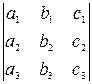
отличен от нуля.
В трехмерном пространстве с введенной декартовой системой координат в качестве базиса часто берут тройку векторов 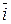 ,
, 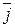 ,
, 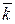 , которые будучи отложенными из начала координат лежат на соответствующих координатных осях, направлены в положительных направлениях этих осей и имеющие единичную длину. Очевидно, что такие векторы некомпланарны и, следовательно, образуют базис. Заметим, что в таком базисе координаты любого вектора есть величины его проекций на соответствующие координатные оси. Также очевидно, что сами векторы
, которые будучи отложенными из начала координат лежат на соответствующих координатных осях, направлены в положительных направлениях этих осей и имеющие единичную длину. Очевидно, что такие векторы некомпланарны и, следовательно, образуют базис. Заметим, что в таком базисе координаты любого вектора есть величины его проекций на соответствующие координатные оси. Также очевидно, что сами векторы 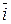 ,
, 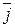 , и
, и 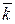 в таком базисе имеют следующие координаты:
в таком базисе имеют следующие координаты:
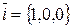 ,
,
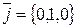 ,
,
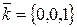 .
.
Определитель, составленный из координат этих векторов, отличен от нуля:
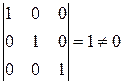 ,
,
Что еще раз доказывает правильность выбранного базиса.
Пусть зафиксирован некоторый базис 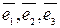 в трехмерном пространстве. Напомним свойства координат векторов, рассматриваемые в курсе линейной алгебры.
в трехмерном пространстве. Напомним свойства координат векторов, рассматриваемые в курсе линейной алгебры.
1. Вектор является нулевым тогда и только тогда, когда все координаты этого вектора равны нулю.
2. При сложении двух векторов складываются соответствующие координаты этих векторов.
3. При умножении вектора на число каждая координата вектора умножается на это число.
4. Два вектора равны друг другу тогда и только тогда, когда равны их соответствующие координаты.
Справедливо также следующее утверждение.
Теорема.Пусть в декартовой прямоугольной системе координат в пространстве заданы две точки 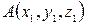 и
и 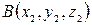 . Тогда
. Тогда
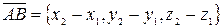 .
.
Доказательство. Осуществим параллельный перенос системы координат так, чтобы начало новой системы совпало с точкой 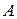 . Тогда в новой системе координат имеем:
. Тогда в новой системе координат имеем:
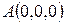 ,
, 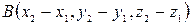 .
.
Спроектируем точку 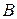 на координатные оси. В результате получим точки
на координатные оси. В результате получим точки 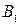 ,
, 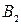 и
и 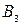 соответственно. Очевидно, что
соответственно. Очевидно, что
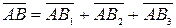 .
.
Кроме того,
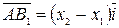 ,
,
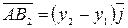 ,
,
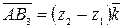 .
.
Следовательно,
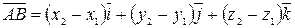
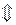
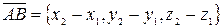 .
.
