Второй замечательный предел, примеры нахождения, задачи и подробные решения
Второй замечательный предел имеет вид:
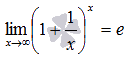
или в другой записи
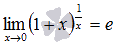
В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность 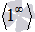 .
.
Разберем несколько примеров нахождения предела по второму замечательному пределу сподробным оприсанием решения.
Пример.
Вычислить предел 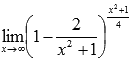
Решение.
Подставляем бесконечность:
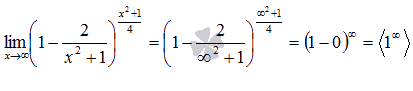
Пришли к неопределенности единица в степени бесконечность. Смотрим в таблицу неопределенностей для определения метода решения и останавливаемся на применении второго замечательного предела.
Сделаем замену переменных. Пусть
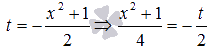
Если 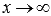 , то
, то 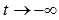
Исходный предел после замены примет вид:
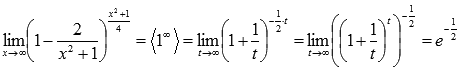
Ответ:
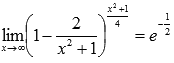
Пример.
Вычислить предел 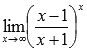
Решение.
Подставляем бесконечность:
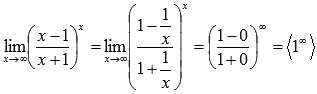
Пришли к неопределенности единица в степени бесконечность, которая указывает на применение второго замечательного предела. Выделим целую часть в основании показательно степенной функции:
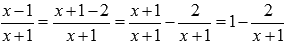
Тогда предел запишется в виде:
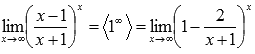
Сделаем замену переменных. Пусть
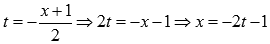
Если 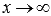 , то
, то 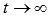
Исходный предел после замены примет вид:
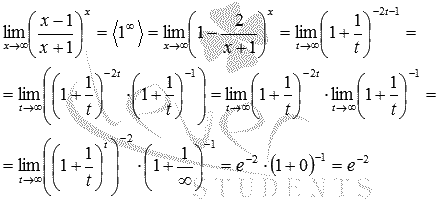
В преобразованиях были использованы свойства степени и свойства пределов.
Ответ:
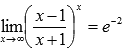
Пример.
Вычислить предел 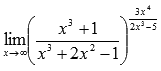
Решение.
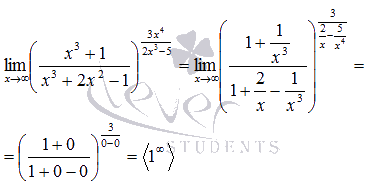
Преобразуем функцию, чтобы применить второй замечательный предел:
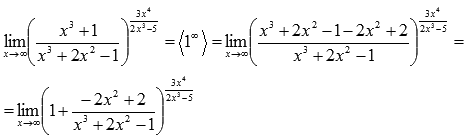
Сейчас домножим показатель на 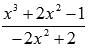 и разделим на это же выражение, затем используем свойства степени:
и разделим на это же выражение, затем используем свойства степени:
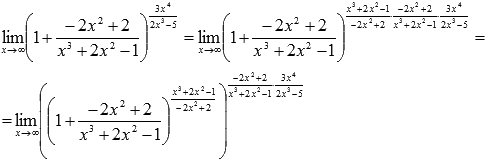
Так как показатели степени числителя и знаменателя дроби 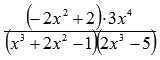 одинаковые (они равны 6), то предел этой дроби на бесконечности равен отношению коэффициентов при старших степенях (см. непосредственное вычисление пределов):
одинаковые (они равны 6), то предел этой дроби на бесконечности равен отношению коэффициентов при старших степенях (см. непосредственное вычисление пределов):
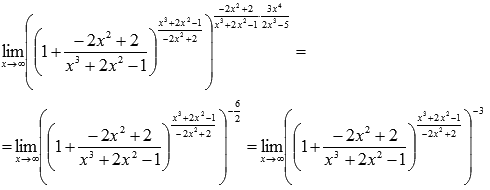
Если произвести замену 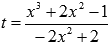 , то получим второй замечательный предел в чистом виде, следовательно,
, то получим второй замечательный предел в чистом виде, следовательно,
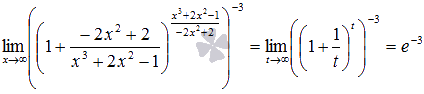
Ответ:
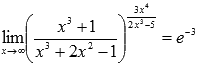
39.
Пусть 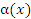 и и 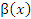 – бесконечно малые функции при – бесконечно малые функции при 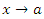 . Предел отношения этих величин может принимать любые значения – в зависимости от быстроты убывания одной величины относительно другой. Для сопоставления скоростей убывания этих величин при стремлении x точке a можно использовать предел отношения . Предел отношения этих величин может принимать любые значения – в зависимости от быстроты убывания одной величины относительно другой. Для сопоставления скоростей убывания этих величин при стремлении x точке a можно использовать предел отношения 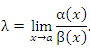 Если этот предел представляет собой конечное ненулевое число, то Если этот предел представляет собой конечное ненулевое число, то 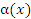 и и 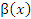 называются бесконечно малыми одного и того же порядка. Особый интерес представляет частный случай, когда λ = 1. Тогда говорят, что называются бесконечно малыми одного и того же порядка. Особый интерес представляет частный случай, когда λ = 1. Тогда говорят, что 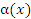 и и 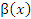 являются эквивалентными бесконечно малыми при являются эквивалентными бесконечно малыми при 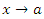 и записывают это утверждение в виде и записывают это утверждение в виде 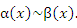 Если λ = 0, то говорят, что Если λ = 0, то говорят, что 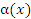 является бесконечно малой более высокого порядка по сравнению с является бесконечно малой более высокого порядка по сравнению с 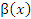 при при 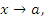 а функция а функция 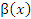 имеет меньший порядок малости. Термин “порядок малости” допускает уточнение, если имеет меньший порядок малости. Термин “порядок малости” допускает уточнение, если 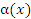 и и 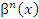 представляют собой бесконечно малые одного и того же порядка. В этом случае говорят, что представляют собой бесконечно малые одного и того же порядка. В этом случае говорят, что 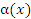 является бесконечно малой n-го порядка по сравнению с является бесконечно малой n-го порядка по сравнению с 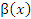 . Например, функция . Например, функция 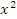 является бесконечно малой 4-го порядка по сравнению с является бесконечно малой 4-го порядка по сравнению с 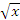 при x → 0. Если λ = ∞, то бесконечно малые при x → 0. Если λ = ∞, то бесконечно малые 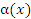 и и 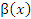 как бы меняются своими ролями. В этом случае функция как бы меняются своими ролями. В этом случае функция 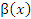 является бесконечно малой более высокого порядка по сравнению с является бесконечно малой более высокого порядка по сравнению с 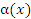 при при 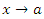 . Сформулируем некоторые полезные свойства эквивалентных бесконечно малых. . Сформулируем некоторые полезные свойства эквивалентных бесконечно малых.
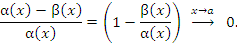 Для записи такого утверждения используется выражение Для записи такого утверждения используется выражение 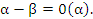
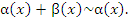 |
40.

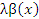 являются эквивалентными, если
являются эквивалентными, если