Геометрическая интерпретация комплексного числа
Множества. Действия над множествами.
Множество представляет собой соединение, совокупность, собрание некоторых предметов, объединенных по какому-либо признаку.
Если любой элемент множества В является и элементом множества А, то множество В называют подмножество множества А.
Действия над множествами:
1. Объединение множеств (А U В).
Объединением множества А и В назыв. такое множество С, которое состоит из всех элементов множеств А и В, и только из них. В этом случае пишут: А U В.
2. Вычитание множеств:
Множество С, которое состоит из всех элементов множества А, не принадлеж. множеству В, назыв. разностью множеств А и В и обознач. А \ В.
Если А принадл.В, то разность А \ В назыв. дополнением множества В до множества А.
2. Метод математической индукции.
Принцип матем.индукции:
Предложение p(n) считается истинным для всех натуральных значений переменной, если выполнены следующие 2 условия:
1). Предложение p(n) истинно для n=1.
2). Для любого натурального k из предположения, что p(n) истинно для n=k следует, что оно истинно и для n=k+1.
Под методом матем.индукции понимают способ доказательства, основанный на принципе матем.индукции, т.е. если требуется доказать истинность предложения p(n) для всех натуральных значений n, то сначала проверяют истинность высказывания p(1), и затем, допустив истинность высказывания p(k), доказывают истинность высказывания p(k+1).
Обобщение метода матем.индукции.
Иногда метод маетм.индукции применяют для доказательства истинности предложения p(n) не для всех натуральн.значений n, а для всех n, начиная с некоторого натурального числа m. В таких случаях сначала проверяется истинность высказывания p(m).
Сочетания. Формула числа сочетаний.
Произведение последовательных натуральн.чисел от единицы до n называется n-факториалом, и обозначается n!.
Напр., 1*2*3*n=n!.
Сочетанием из n-элементов по k-элементов называется любое подмножество из k элементов множества, содержащего n элементов.
Число сочетаний из n-элементов по k элементов обозначается Ckn, и вычисл.по формуле Ckn=n!/k!(n-k)!
Свойства сочетаний:
1. Ckn =Cn-kn
2. Ckn + Ck+1n+1
Бином Ньютона.
Формула Бинома Ньютона позволяет возводит двучлен а+в в любую натуральную степень n.
Ньтоном было установлено, что (a+b)n=C0nanbn+ C1nan-1bn-1+ C2nan-2bn-2 +…+Cknan-kbn-k + … + Cnna0bn, где Ckn – число сочетаний.
Эта формула позволяет возводить двучлен в любую стпень, доказывается методом математич. индукции.
Если необходимо найти член разложеня с номером k, то он будет вычисляться по формуле: Ck-1nan-(k-1)bk-1 .
Действительные числа. Модуль действительного числа.
Множество всех конечных и бесконечных десятичных дробей называется множеством действительных чисел, а каждая такая дробь называется действительным числом.
Модулем действит.числа называется число a является само число a, если оно положительное или равно 0, и число –a, если оно отрицательное.
│a│= a, если a≥0
- a, если a<0
Комплексные числа. Операции над компл. числами в алгебр.форме.
Действит.чисел не достаточно для решения многих практических задач. Простейшее квадратн.уравнение x2+1=0 во множестве действит.чисел решить нельзя. Для расширения понятия числа ввели обозначение √-1=i, и назвали "мнимой единицей", т.е. x2=-1.
Комплексным числом z назыв.число вида a+bi, где a и b – действит.числа, а i – мнимая единица. 2 комплексн.числа z1=a+bi и z2=c+di считаются равными, если равны их действит.части и коэффициенты при мнимых частях (a=c, b=d).
Числа z1=a+bi и z2=a-bi назыв. сопряженными.
Числа z1=a+bi и z2=-a-bi назыв. противоположными.
Операции над комплексн.числами (z1=a+bi, z2=c+di);:
1). Сложение: z1+z2=(a+bi)+(c+di)=(a+c)+i(b+d). Для сложениянеобход. сложить их действит.части и коэффициенты при мнимых частях.
2). Вычитание: z1-z2=(a+bi)-(c-di)=(a-c)+i(b-d).
3). Умножение: z1*z2=(a+bi)*(c+di)=(ac)+adi+cbi+bdi2=ac+i(ad*cb)-bd . !(bdi2=-bdi).
4). Деление: z1/z2=a+bi/c+di=(a+bi)(c-di)/(c+di)(c-di)=ac-adi+bci-bdi2/c2-d2i2=ac+bd+(bc-
- ad)i/c2+d2=ac+bd/c2+d2 + (bc-ad)i/ c2+d2
Геометрическая интерпретация комплексного числа.
Т.к каждому комплексн.числу z=a+bi соответствует пара действит.числе a и b, а каждой паре действит.чисел на плоскости соответств. единственная точка, то комплексные числа можно изображать точками координатн.плоскости. На оси абсцисс (ОХ) откладывается действит.часть (a), поэтому эту ось назыв.действительной осью; на оси ординат (ОУ) откладывается коэффициент при мнимой части, поэтому эту ось назыв. мнимой.
Т.к. каждому комплексн.числу z=a+bi соотв. единственная точка с координатами (a;b), а каждой точке плоскости соотв. свой радиус вектор,то комплексн. числа можно изображать при помощи векторов
Длина радиусвектора соотв.комплексн. числу z=a+bi, назыв. модулем комплексн.числа и обознач. r, а угол, образован.радиус-вектором с положит.направлением ОХ, назыв. аргументом комплексн.числа и обознач. arg z:
│z│=r= √a2+b2.
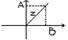 z=a+bi
z=a+bi
b/r=sin φ a/r=cos φ
