Интегрирование функций комплексного переменного

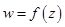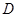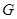Пусть однозначная функция определена и непрерывна в области , а – кусочно-гладкая кривая, лежащая в 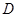, , 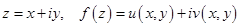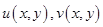- действительные функции переменных 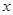и 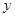. В этом случае вычисление интеграла от функции 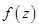комплексного переменного 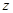сводится к вычислению криволинейных интегралов от функций действительных переменных:

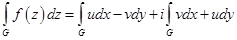
Если кривая 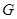задана параметрическими уравнениями

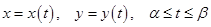
То

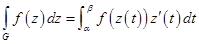
Где

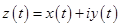
Если 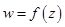- аналитическая функция в односвязной области 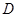, то интеграл не зависит от пути интегрирования, а зависит только от положения начальной и конечной точек интегрирования. В этом случае для вычисления интеграла можно использовать формулу Ньютона-Лейбница.

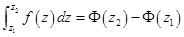
Где 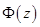- первообразная для функции 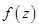, т.е.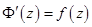

Если функция является аналитической в области 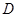, ограниченной кусочно-гладких замкнутым контуром 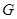, и на самом контуре 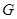, то

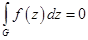
А для любой внутренней точки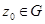

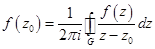
Степенной ряд с комплексными числами

Ряд 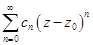, где 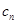- комплексные числа, называется степенным по степеням .

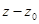Если степенной ряд сходится в точке 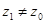, то он абсолютно сходится для всех 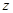таких, что 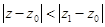, при этом сходимость будет равномерной в любом замкнутом круге 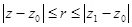. Если же ряд расходится в точке 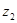, то он расходится для всех 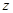таких, что .

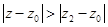Таким образом, областью сходимости степенного ряда является круг с центром в точке 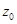, радиус которого может быть определен с использованием признака Даламбера или признака Коши, т.е. из соотношений

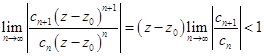
Или

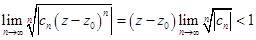
Отсюда для вычисления радиуса 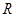круга сходимости имеют место соотношения

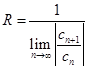или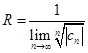

В точках окружности 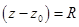степенной ряд может расходиться, сходиться абсолютно или сходиться условно. Для оценки сходимости ряда в этих точках используются признаки сходимости числовых рядов.

Если 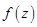- функция аналитическая в круге 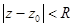, то она представима в этом круге рядом Тейлора вида:

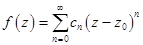
коэффициенты которого определяются по формулам:

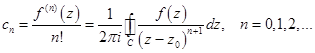
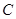- окружность с центром 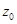, лежащим внутри круга аналитичности функции.

Если 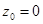ряд Тейлора называется рядом Маклорена. Имеют место следующие основные разложения элементарных функций в ряд Маклорена:

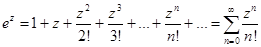
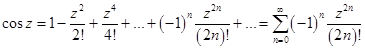
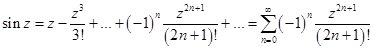
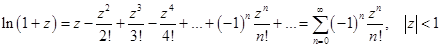
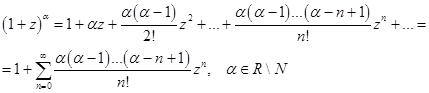
Первые три разложения имеют место во всей комплексной плоскости, последние два разложения справедливы внутри круга .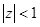

Ряд Лорана

Функция 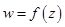однозначная и аналитическая в кольце 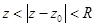разлагается в этом кольце в ряд Лорана:

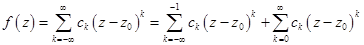
Где коэффициенты определяются по формуле

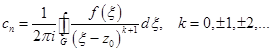
Здесь 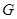– окружность с центром 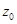, лежащая внутри кольца.

Разложение в ряд Лорана для данной функции единственно.

Ряд 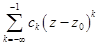называется главной частью ряда Лорана, ряд 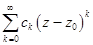называется правильной частью ряда Лорана.

На практике для построения ряда Лорана чаще всего используют основные разложения элементарных функций в ряд Тейлора.

Например, разложим в ряд Лорана в кольце 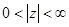функцию

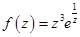
Имеем основное разложение

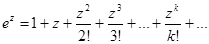
Тогда

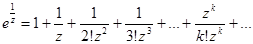
Тогда ряд Лорана имеет вид:

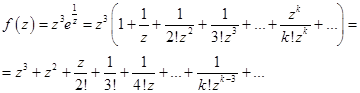
В силу единственности ряда Лорана полученное разложение функции 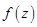по степеням 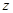является рядом Лорана для функции 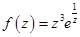в кольце .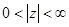