Интегрирование функций комплексного переменного

1. Основные понятия и утверждения

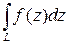Теорема 5.1(достаточное условие существования интеграла от функции комплексного переменного). Пусть L – простая гладкая кривая на , f(z)=u(x;y)+i×v(x;y) непрерывна на L. Тогда существует , причем справедливо равенство:

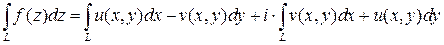. (5.1)

Теорема 5.2. Пусть L – простая гладкая кривая, заданная параметрически: L: z(t)=x(t)+i×y(t), a£t£b, функция f(z) непрерывна на L. Тогда справедливо равенство:

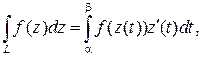(где 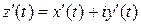). (5.2)

Теорема 5.3.Если f(z) аналитическая в области D функция, то 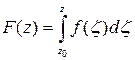- аналитическая функция и F'(z)=f(z), где интеграл берётся по любой кусочно-гладкой кривой, соединяющей точки z₀ и z.

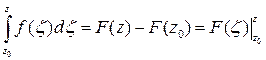- формула Ньютона-Лейбница.

2. Способы вычисления интеграла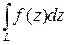

Первый способ. Вычисление интегралов 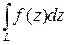от непрерывной функции путем сведения к криволинейным интегралам от функций действительных переменных (применение формулы (5.1)).

1. Найти Ref=u, Imf=v.

2. Записать подынтегральное выражение f(z)dz в виде произведения (u+iv)(dx+idy)=udx-vdy+i(udy+vdx).

3. Вычислить криволинейные интегралы вида 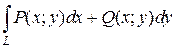по правилам вычисления криволинейных интегралов второго рода.

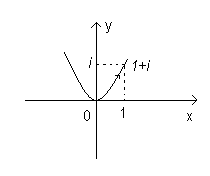
Пример 5.1. Вычислить 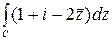по параболе y=x² от точки z₁=0 до точки z₂=1+i.

■ Найдем действительную и мнимую части подынтегральной функции. Для этого подставим в выражение для f(z) z=x+iy:

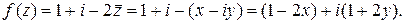
Тогда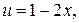

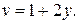
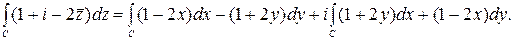
Так как y=x², то dy=2x, 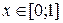. Поэтому

. ■

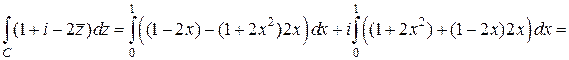
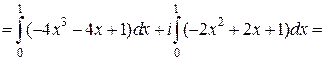
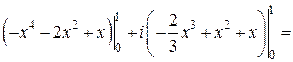
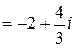Второй способ. Вычисление интегралов 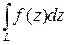от непрерывной функции путем сведения к определенному интегралу в случае параметрического задания пути интегрирования (применение формулы (5.2)).

1. Записать параметрическое уравнение кривой z=z(t) и определить пределы интегрирования: t=a соответствует начальной точке пути интегрирования, t=b - конечной.

2. Найти дифференциал комплекснозначной функции z(t): dz=z¢(t)dt.

3. Подставить z(t) в подынтегральное выражение, преобразовать интеграл к виду: .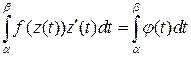

4. Вычислить полученный определенный интеграл.

Пример 5.2. Вычислить 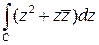, где С - дуга окружности , .

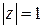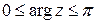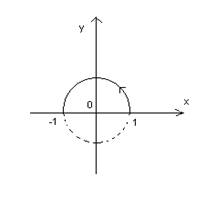
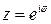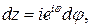
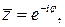
■ Параметрическое уравнение данной кривой: , 0£j£p. Тогда 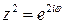. Получаем

. ■

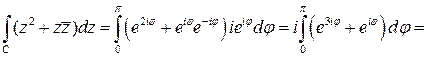
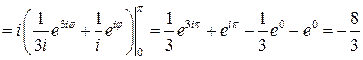Пример 5.3. Вычислить 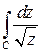, где С – верхняя дуга окружности 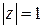при условии: а) 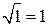,б) .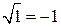

■ Задание значений функции 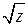в контуре интегрирования позволяет выделить однозначные ветви выражения 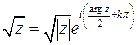, k=0,1. Так как при 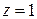имеем 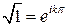, k=0,1,то в первом случае выделяем ветвь с k=0, а во втором – с k=1.

Подынтегральная функция на контуре интегрирования непрерывна. Параметрическое уравнение данной кривой: 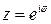, 0£j£p. Тогда .

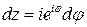а) Ветвь определяется при k=0, то есть из 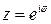получаем .

.

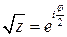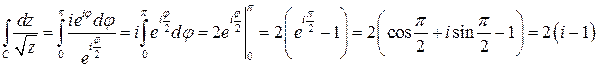б) Ветвь определяется при k=1, то есть из 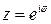получаем .

. ■

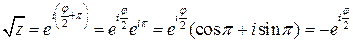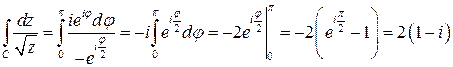Третий способ. Вычисление интегралов от аналитических функций в односвязных областях (применение формулы (5.3)).

Найти первообразную F(z), используя свойства интегралов, табличные интегралы и методы, известные из действительного анализа. Применить формулу Ньютона-Лейбница: .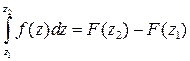

Пример 5.4. Вычислить 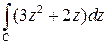, где С – прямая АВ, z_А=1-i, z_В=2+i.

■ Так как подынтегральная функция 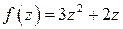- аналитическая на всей комплексной плоскости, то применим формулу Ньютона-Лейбница

. ■

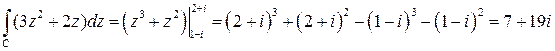3. Основные теоремы интегрального исчисления

функций комплексного переменного

Теорема 5.4 (Коши).Если f(z) аналитическая в односвязной области G функция, то 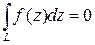, где L- любой замкнутый контур, лежащий в G.

Теорема Коши имеет место и для многосвязной области.

Теорема 5.5.Пусть функция f(z) аналитическая в односвязной области D, L-произвольный замкнутый кусочно-гладкий контур, лежащий в D. Тогда для любой точки z₀, лежащей внутри контура L, справедлива формула:

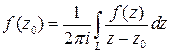, (5.4)

где L обходится в положительном направлении.

Формула (5.4) называется интегральной формулой Коши. Она выражает значения аналитической функции внутри контура через её значения на контуре.

Теорема 5.6.Всякая функция f(z), аналитическая в области D, имеет производные всех порядков на этой области, и для "z₀ÎD справедлива формула:

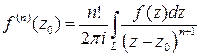, (5.5)

где L – произвольный кусочно-гладкий замкнутый контур, целиком лежащий в D и содержащий внутри себя точку z₀.

4.Вычисление интегралов по замкнутому контуру

от функций комплексного переменного

Рассмотрим интегралы вида 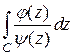, где функция j(z) аналитическая в 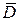, а y(z) – многочлен, не имеющий нулей на замкнутом контуре С.

Правило.При вычислении интегралов вида 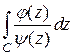в зависимости от кратности нулей многочлена y(z) и их расположения относительно контура С можно выделить 4 случая.

1. В области D нет нулей многочлена y(z). Тогда функция 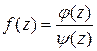аналитическая и по теореме Коши .

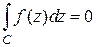2. В области D расположен один простой нуль z=z₀ многочлена y(z). Тогда записываем дробь в виде 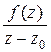, где f(z) – функция аналитическая в 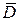Применяя интегральную формулу Коши (5.4), получаем

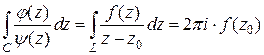. (5.6)

3. В области D расположен один кратный нуль z=z₀ многочлена y(z) (кратности n). Тогда записываем дробь в виде 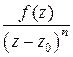, где f(z) – функция аналитическая в Применяя формулу (5.5), получаем

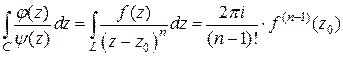. (5.7)

4. В области D расположены два нуля многочлена y(z) z=z₁ и z=z₂. Тогда подынтегральную функцию представляем в виде суммы двух дробей, а интеграл в виде суммы двух интегралов, каждый из которых вычисляем в соответствии с п.2 или п.3.

Пример 5.5. Вычислить 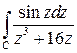, где С – окружность .

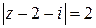■ Находим нули знаменателя – особые точки подынтегральной функции 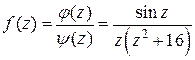. Это точки 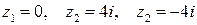. Далее определяем расположение точек относительно контура интегрирования: ни одна из точек не входит в область, ограниченную окружностью с центром в точке 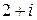и радиусом 2 (то есть имеем первый случай). В этом можно убедиться, выполнив чертёж или определив расстояние от каждой из точек до центра круга и сравнив с величиной радиуса. Например, для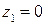 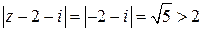, поэтому 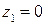не принадлежит кругу.

Тогда функция 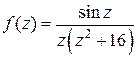аналитическая в круге 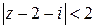, и по теореме Коши .

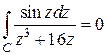Заметим, что заданный интеграл равен нулю и для любого другого контура, ограничивающего область, в которую не входит ни один из нулей знаменателя. ■

Пример 5.6. Вычислить 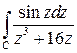, где С – окружность .

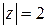■ Рассуждая, как в примере 5.5, находим, что в круге 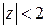расположен только один из нулей знаменателя 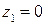(второй случай). Поэтому записываем подынтегральную функцию в виде 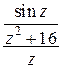, функция 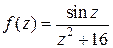аналитическая в круге 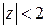. Тогда по формуле (5.6)

.■

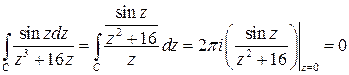Пример 5.7. Вычислить 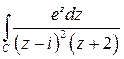, где С – окружность .

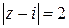■ Находим нули знаменателя – особые точки подынтегральной функции 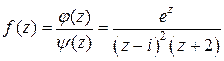. Это точки 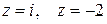. В области 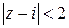расположен один нуль 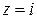кратности 2многочлена 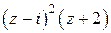(третий случай). Поэтому записываем подынтегральную функцию в виде 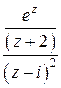, функция 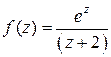аналитическая в 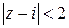. Тогда по формуле (5.7):

. ■

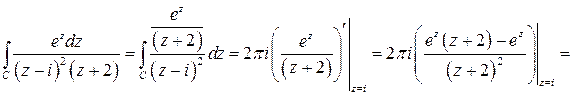
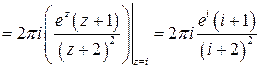Пример 5.8.Вычислить 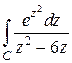, где С – окружность .

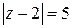■ В области, ограниченной окружностью с центром в точке 2 радиуса 5, имеем две точки z=0и z=6, в которых знаменатель подынтегральной функции обращается в нуль (четвертый случай) (четвертый случай). Непосредственно применить формулу (5.6) нельзя. Разложим дробь 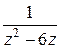на сумму простейших: .

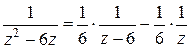Подставляя в интеграл, получим

.

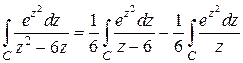Каждый из интегралов в правой части, вычисляем по формуле (5.6). В каждом случае 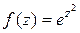- аналитическая во всей комплексной плоскости функция.

. ■
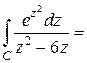
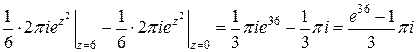