Вычисление пределов функций. Раскрытие неопределенностей
Правило.Для вычисления предела функции 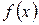 в точке
в точке 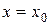 или при
или при 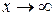 надо применить теоремы о пределах и подставить предельное значение аргумента.
надо применить теоремы о пределах и подставить предельное значение аргумента.
Для всех основных элементарных функций в любой точке их области определения имеет место равенство
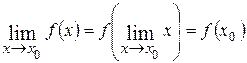 .
.
Примеры
Найти пределы функций:
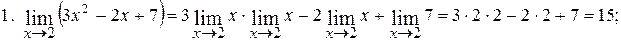
2. 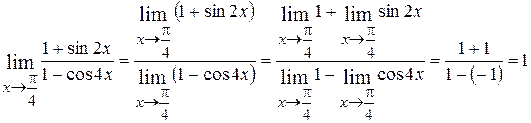 ;
;
3. 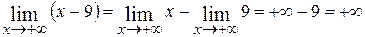 ;
;
4. 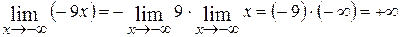 ;
;
5. 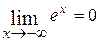 .
.
При вычислении пределов функций формальная подстановка вместо х предельного значения 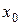 часто приводит к неопределенным выражениям вида:
часто приводит к неопределенным выражениям вида: 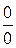 ,
, 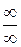 ,
, 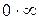 ,
, 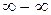 ,
, 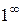 ,
, 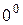 ,
, 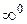 .
.
Например, 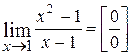 или
или 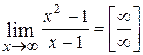 .
.
Выражения вида 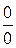 ,
, 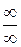 ,
, 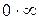 ,
, 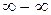 ,
, 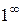 ,
, 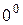 ,
, 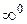 называются неопределенностями.
называются неопределенностями.
Вычисление предела функции в этих случаях называют раскрытием неопределенности.
Рассмотрим правила раскрытия таких неопределенностей.
Неопределенность вида 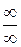
Если 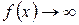 и
и 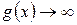 при
при 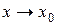 (
( 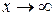 ), то говорят, что их частное
), то говорят, что их частное 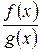 представляет собой неопределенность вида
представляет собой неопределенность вида 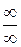 .
.
Правило.Чтобы раскрыть неопределенность вида 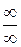 , заданную отношением двух многочленов, надо и числитель и знаменатель разделить на самую высокую входящую в них степень х.
, заданную отношением двух многочленов, надо и числитель и знаменатель разделить на самую высокую входящую в них степень х.
Например, 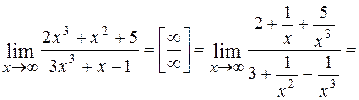
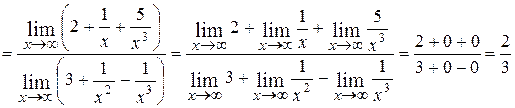 .
.
Рассмотрим дробно−рациональную функцию
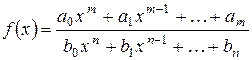 (
( 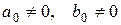 ),
),
представляющую собой отношение двух многочленов относительно х степеней m и n соответственно, и исследуем поведение этой функции при 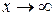 .
.
При нахождении предела данной функции при 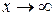 могут иметь место три варианта ответа:
могут иметь место три варианта ответа:
| 1. | 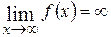 , если , если 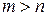 ; ; |
| 2. | 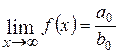 , если , если 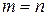 ; ; |
| 3. | 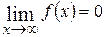 , если , если 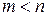 . . |
Из этого следует, что предел отношения двух многочленов при 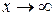 во всех случаях равен пределу отношения их старших членов.
во всех случаях равен пределу отношения их старших членов.
Примеры
Найти пределы функций:
1. 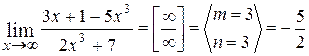 ;
;
2. 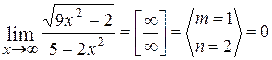 ;
;
3. 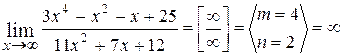 .
.
Неопределенность вида 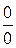
Если требуется найти 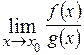 , где
, где 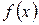 и
и 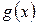 − бесконечно малые функции при
− бесконечно малые функции при 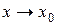 (
( 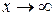 ), т.е.
), т.е. 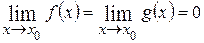 , то в этом случае вычисление предела называют раскрытием неопределенности вида
, то в этом случае вычисление предела называют раскрытием неопределенности вида 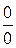 .
.
Рассмотрим возможные приемы раскрытия такой неопределенности.
Выделение критического множителя
Правило.Чтобы раскрыть неопределенность вида 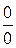 , заданную отношением двух многочленов, надо и в числителе и в знаменателе выделить критический множитель и сократить на него дробь.
, заданную отношением двух многочленов, надо и в числителе и в знаменателе выделить критический множитель и сократить на него дробь.
Примеры
Найти пределы функций:
1. 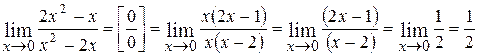 ;
;
2. 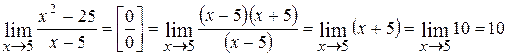 ;
;
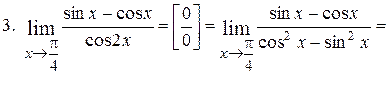
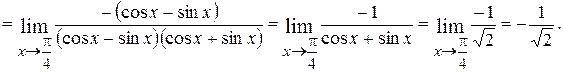
Преобразование иррациональных выражений
Правило.Чтобы раскрыть неопределенность вида 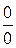 , в которой числитель или знаменатель, или тот и другой иррациональны, надо:
, в которой числитель или знаменатель, или тот и другой иррациональны, надо:
− перенести иррациональность из числителя в знаменатель, или из знаменателя в числитель, домножив дробь на сопряженные выражения,
− либо сделать замену переменной.
Замечание.
Если под знаком предела делается замена переменной, то все величины, входящие под знак предела, должны быть выражены через эту новую переменную. Из равенства, выражающего зависимость между старой переменной и новой, должен быть определен предел новой переменной.
Примеры
Найти пределы функций:
1. 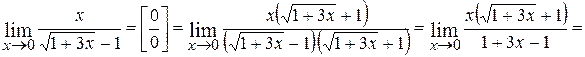
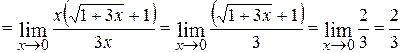 ;
;
2. 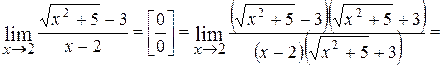
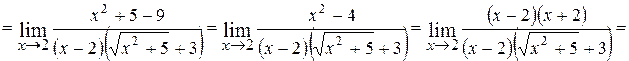
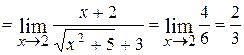 ;
;
3. 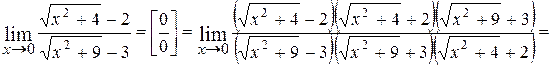
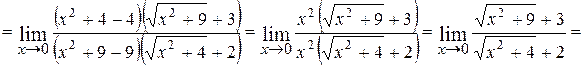
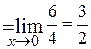 ;
;
4. 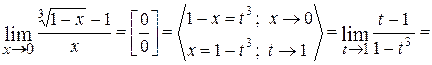
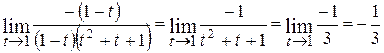 .
.
