Дополнительные ортогональные проекции
Информация была взята с сайта: http://www.spbgasu.ru/
ПРЯМАЯ. ПЛОСКОСТЬ
Задача № 1.1. Разделить отрезок АВ точкой С в отношении 
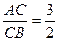
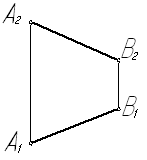
Рис. 1
Так как делению отрезка в каком-либо отношении соответствует такое же деление его проекций, то делим проекцию А1В1(можно было бы начать и с фронтальной проекции) на 5 частей. Для этого через точку А1 проводим произвольную прямую и откладываем на ней пять каких-либо равных между собой отрезков. Точку 5 соединяем с точкой В1.Через точку 3 проводим прямую, параллельную прямой В1-5 до пересечения с А1В1в точке С1. По точке С1строим проекцию С2. В точке С отрезок АВ разделен в отношении 3 : 2, считая от точки А.
Задача№ 1.2. Найти недостающую проекциюточкиК, лежащей на прямой (АВ).
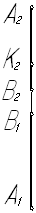
Рис. 2
Чтобы построить горизонтальную проекцию К1 точки К, принадлежащей профильной прямой (АВ), следует воспользоваться свойством операции проецирования - отношение длин отрезков, лежащих на одной и той же прямой или на параллельных прямых, равно отношению длин проекций этих отрезков. На основании этого свойства точка К будет принадлежать прямой (АВ), если её проекции К1 и К2 будут делить отрезки А1В1 и А2В2 в одинаковом отношении. Горизонтальная проекция точки К определена с помощью прямой А0В0, при построении которой прямые А2А0 ççВ2В0 ççК2К0 и А1А0 ççВ1В0 ççК0К1 проведены произвольно.
Задача № 1.3. Через точку К (К1, К2) провести горизонталь h (h1, h2) под углом 30° к плоскости проекций П2 и фронталь f (f1, f2) под углом 45° к плоскости проекций П1.

Рис. 3
Так как все точки прямой h находятся на одинаковом расстоянии от плоскости П1, то на эпюре фронтальная проекция h2 параллельна оси Х12 и проходит через точку К2, а горизонтальная проекция h1 через точку К1 и составляет с осью Х12 угол 30°.
Фронталь f параллельна плоскости проекций П2, следовательно на эпюре горизонтальная проекция f1 фронтали f параллельна оси Х12 и проходит через точку К1, фронтальная проекция f2 фронтали f проходит через точку К2 и составляет с осью проекций Х12 угол 45°.
Задача № 1.4. Через точку К (К1, К2) провести прямую n параллельно прямой m (m1, m2).
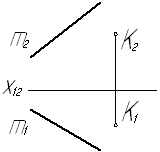
Рис. 4
Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны. Это свойство параллельного проецирования остается справедливым и для ортогональных проекций, т.е. если n ççm, то n1ççm1 и n2 ççm2 и горизонтальная проекция прямой n1 проходит через горизонтальную проекцию К1 точки К, а фронтальная проекция прямой n2 проходит через К2 точки К и n2 ççm2.
Задача № 1.5. Найти недостающие проекции точек М, К, N, лежащих в плоскости α, заданной треугольником АВС.
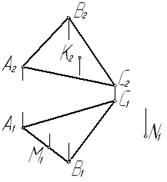
Рис. 5
Известно, что если точка принадлежит плоскости, то она принадлежит какой-либо прямой этой плоскости. Поэтому точку М2 находим на фронтальной проекции А2В2 отрезка АВ на одной линии связи с точкой М1. Для построения точки К1 через точки А2 и К2 проводим фронтальную проекцию вспомогательной прямой l, лежащей в данной плоскости. Получив точку 12, находим точку 11 на проекции В1С1. Теперь проводим прямую из точки А1 через точку 11 и на этой прямой находим горизонтальную проекцию точки К. Аналогично строится точка N2 с помощью вспомогательной прямой m (m1m2), принадлежащей плоскости a.
Задача № 1.6. Построить недостающую проекцию А2В2С2 треугольника АВС, лежащего в плоскости a (h Ç f).
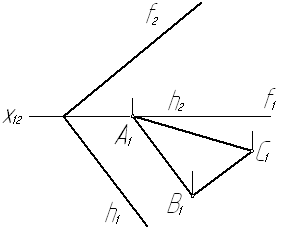
Рис. 6
Чтобы построить фронтальную проекцию треугольника АВС, надо найти фронтальные проекции точек А, В и С. Проекцию А2 находим по линии связи на f2 (фронтальной проекции фронтали f), проекцию В2 строим с помощью горизонтали α, проведенной в плоскости. Сначала проводим проекции α1 параллельно h1 через точку В1, затем через точку А2 - фронтальную проекцию горизонтали α2 параллельно оси Х12 и на ней находим проекцию В2. Фронтальную проекцию точки С находим при помощи фронтали b, хотя конечно, можно было бы и для этой точки применить горизонталь. Через точку С1 проводим горизонтальную проекцию b1 фронтали b параллельно оси Х12, находим точки 11 и 12.. Фронтальная проекция b2 фронтали b проходит через точку 12 параллельно f2; на этой проекции получаем точку С2. Искомая проекция треугольника АВС определяется точками А2, В2 и С2.
Задача № 1.7. Определить в плоскости a(аççb) точку А, расположенную на расстоянии 15 мм от плоскости П1 и 25 мм от плоскости П2.
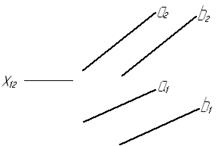
Рис. 7
Для построения точки А, расположенной в плоскости a на определенном расстоянии от плоскостей П1 и П2, необходимо в плоскости провести горизонталь h на расстоянии 15 мм от плоскости проекций П1 и на расстоянии 25 мм от плоскости проекций П2 построить фронталь f . На пересечении горизонтали h и фронтали f находим искомую точку А. На эпюре проводим фронтальную проекцию h2 горизонтали h на расстоянии 15 мм от оси проекций Х12. Отмечаем точки 12 и 22 на проекциях а2 и b2 и находим проекции 11 и 21 на а1 и b1. Горизонтальная проекция h1 горизонтали h проходит через точки 11 и 21. Затем построим горизонтальную проекцию f1 фронтали f на расстоянии 25 мм от оси Х12. Отмечаем точку пересечения прямой h1 с прямой f1 в точке А1, а точка А2 строится по линии связи на прямой h2.
Задача № 1.8. Через точку А (А1А2) провести горизонтально проецирующую плоскость a и фронтально проецирующую плоскость β, параллельные прямой l.
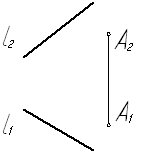
Рис. 8
Прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскости.
Чтобы построить искомые плоскости a и β через точку А, так чтобы эти плоскости были параллельны прямой l, сначала через точку А надо провести прямую m параллельно прямой l; на эпюре m1 строится через точку А1 параллельно l1, а m2 проводится через точку А2 параллельно l2. Затем заключаем прямую m в горизонтально проецирующую плоскость a; на эпюре a1 и горизонтальная проекция плоскости a совпадёт с горизонтальной проекцией m1 прямой m. А чтобы заключить прямую m во фронтально-проецирующую плоскость β на эпюре β2 - фронтальная проекция плоскости β совпадет с фронтальной проекцией m2 прямой m.
Решения типовых задач приведены на с.8.
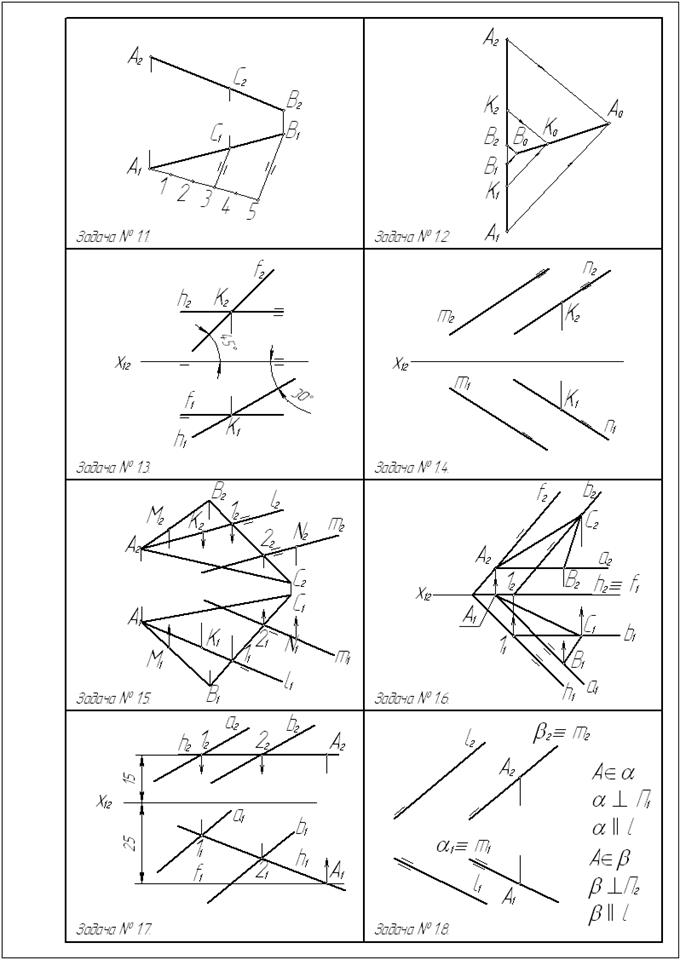
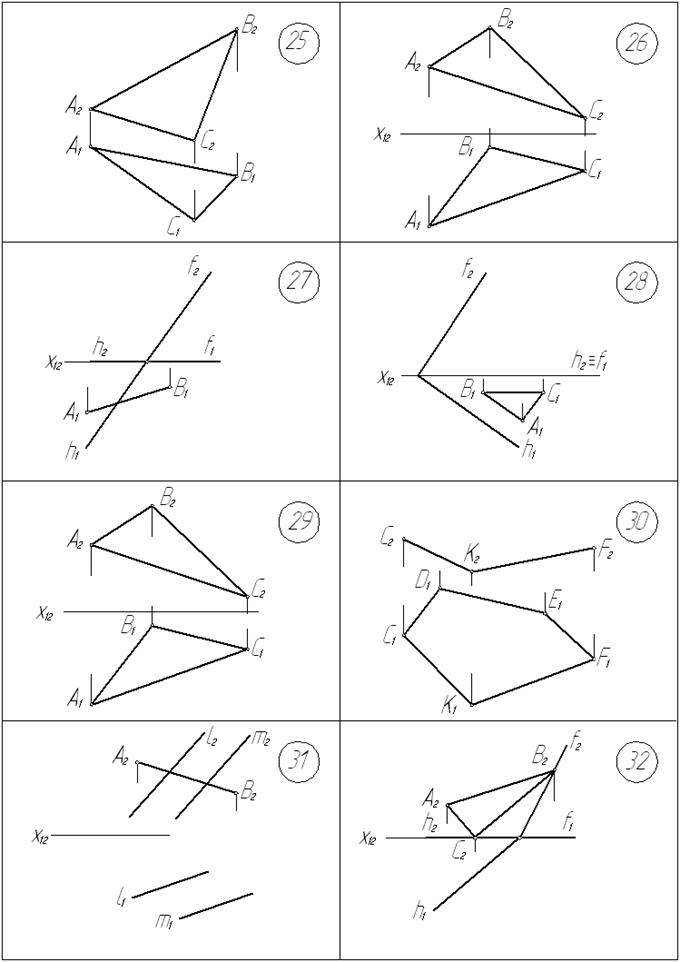
Условия задач
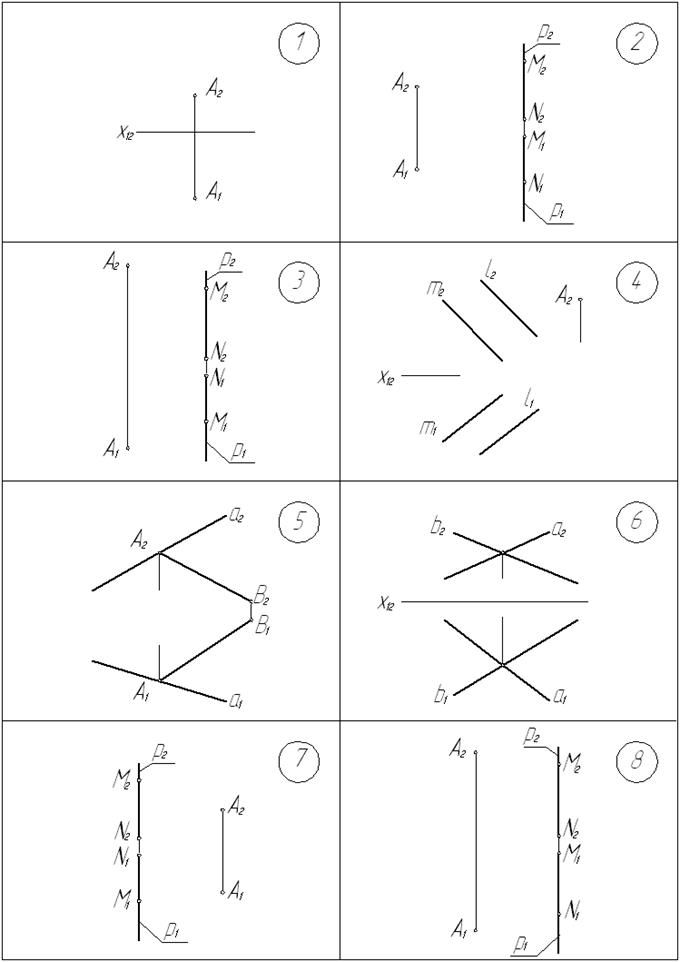
Графические условия задач приведены на с. 10… 13.
1. Через точку А провести плоскость, заданную линии уровня.
2. Через точку А провести прямую l, параллельную прямой р.
3. Через точку А провести горизонталь, пересекающую данную прямую р.
4. Через точку А, фронтальная проекция которой А2 задана, провести прямую n, лежащую в плоскости a(mççl) и параллельную прямым m и l.
5. Построить точку С, которая делит отрезок АВ в отношении АС : СВ = 1:2, и через эту точку провести прямую l, параллельную прямой а.
6. В плоскости a(аÇb) построить точку А, удаленную от плоскости П1 на расстояние 20 мм и от плоскости П2 - на 45 мм.
7. Через точку А провести прямую l, параллельную прямой р.
8. Через точку А провести прямую l, параллельную прямой р.
9. Через точку А провести горизонталь и фронталь, пересекающие данную прямую l.
10. В плоскости a(аÇb) построить точку А, удаленную от плоскостей П1 и П2 на расстояние 30 мм.
11. Через точку А провести горизонталь h и фронталь f.
12. В плоскости a(l ççm) построить точку А, удаленную от плоскости П1 на расстояние 20 мм и от плоскости П2 - на 15 мм.
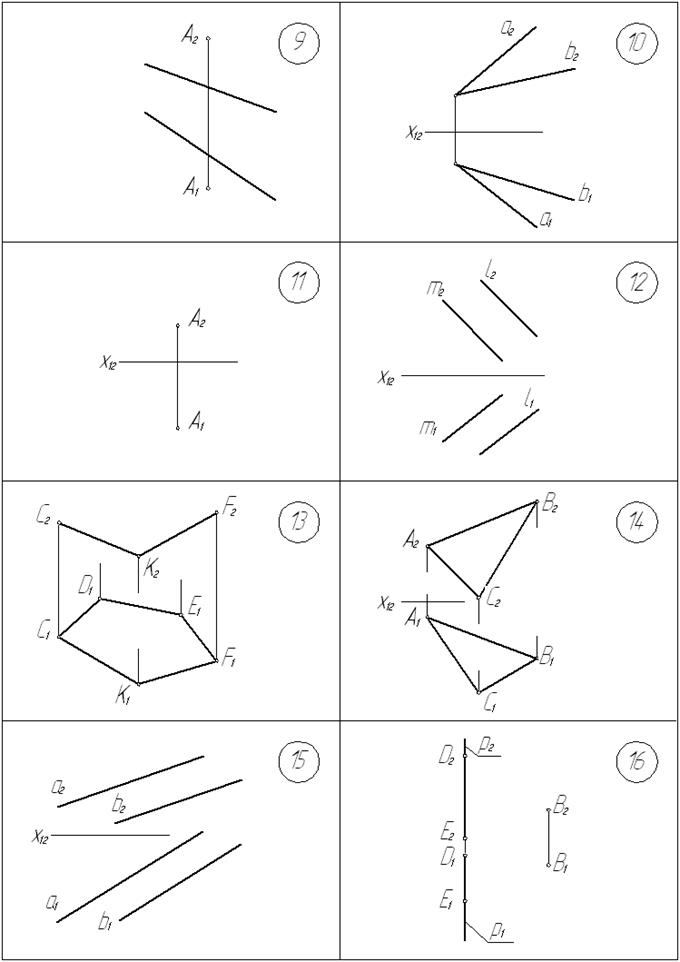
13. Достроить фронтальную проекцию плоской фигуры.
14. В плоскости a (АВС) провести горизонталь, отстоящую от плоскости П1 на 25 мм.
15. В плоскости a(а ççb) построить точку А, удаленную от плоскостей П1 и П2 на расстояние 25 мм.
16. Через точку В провести фронталь, пересекающую данную прямую р.
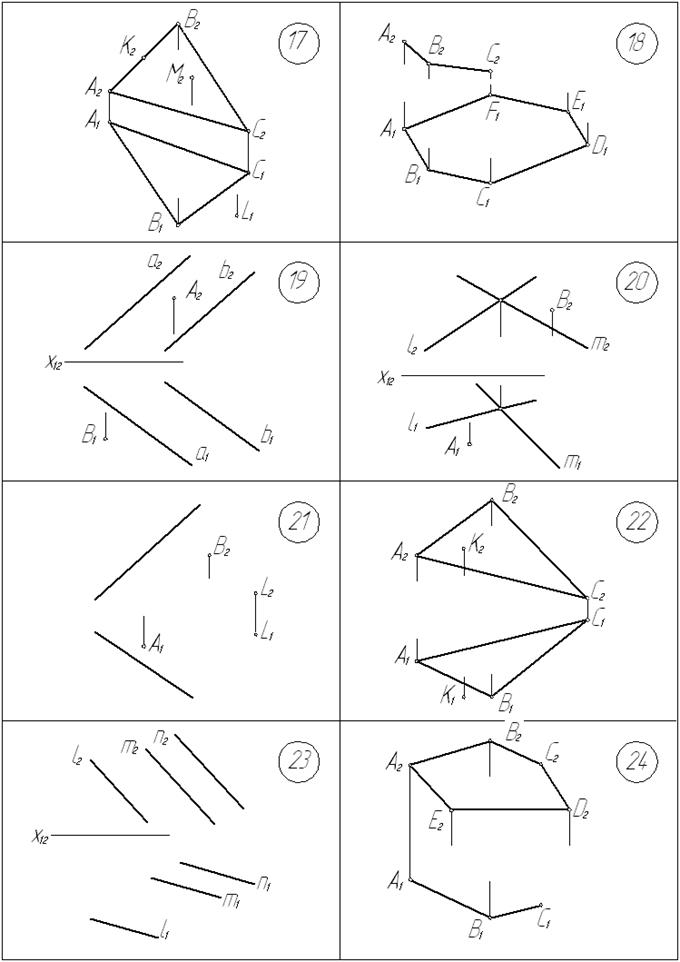
17. В плоскости a (D АВС) достроить проекции точек К, М, l, проекции которых К2, М2, l1 заданы.
18. Достроить фронтальную проекцию плоской фигуры АВСDEF.
19. В плоскости a(а ççb) построить точки А и В, если заданы проекции А2 и В1
20. В плоскости a(lÇm) построить отрезок АВ, проекции А1 и В2 концов которого заданы.
21. В плоскости a(l, L) построить отрезок АВ, проекции А1 и В2 концов которого заданы.
22. Определить, принадлежит ли точка К плоскости a (АВС).
23. Определить, лежат ли параллельные прямые l, m, n в одной плоскости.
24. Достроить горизонтальную проекцию плоскостей фигуры АВСDE.
25. В плоскости a (D АВС) построить горизонталь h (h1, h2) через точку А и фрон- таль f(f1, f2) через точку В.
26. В плоскости a(АВС) провести горизонталь, отстоящую от плоскости П1 на 20 мм.
27. В плоскости a(f Çh) построить отрезок АВ, горизонтальная проекция которого задана.
28. В плоскости a(h Çf) построить DАВС, горизонтальная проекция которого задана
29. В плоскости a(АВС) провести фронталь, отстоящую от плоскости П1 на 30 мм.
30. Достроить фронтальную проекцию плоской фигуры.
31. В плоскости a(l ççm) построить отрезок АВ (А1В1), фронтальная проекция ко- торого задана.
32. В плоскости a(h Çf) построить DАВС (DА1В1С1), фронтальная проекция которого задана.
ДОПОЛНИТЕЛЬНЫЕ ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
Задача № 2.1. Построить дополнительную ортогональную проекцию прямой l на плоскости, параллельной этой прямой.
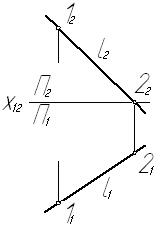
Рис. 9
Для решения задач взята новая плоскость проекций П4, отвечающая двум условиям: П4 ^ П1 и П4 ççl. На эпюре новая ось Х14 проведена параллельно l1. Чтобы построить дополнительную ортогональную проекцию l4 прямой l, отметим на этой прямой две точки, например 1 и 2, и построим их дополнительные проекции 14 и 24.
Задача № 2.2. Построить дополнительную ортогональную проекцию прямой l на плоскости, перпендикулярной этой прямой. Другими словами, в новой системе прямая l должна стать проецирующей.

Рис. 10
Преобразование одной из проекций прямой l общего положения в точку требует двух дополнительных плоскостей проекций, так как в системе П2/П1 плоскость, перпендикулярная l, не будет ортогональной ни к плоскости П2, ни к плоскости П1.
При переходе от системы П1/П2 к системе П1/П4 плоскость П4 располагают перпендикулярно П1 и параллельно прямой l, т.е. решают первую задачу, рассмотренную выше.
При введении второй новой плоскости П5, её располагают перпендикулярно прямой l . Этим самым будет обеспечено условие ортогональности П4/П5. Ось Х45 построена перпендикулярно l4. На плоскости П5 прямая l изобразится точкой. Итак, в системе П4/П5 прямая l стала проецирующей относительно плоскости П5.
