Теореме Чебышева. Теорема Бернулли. ЦПТ

Теорема (Чебышева):Если 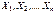– независимы и существует С > 0, такая что 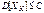, К = 1, 2, …, n, тогда :

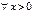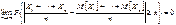
Доказательство:

Рассмотрим 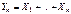и применим к СВ 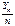второе неравенство Чебышева.

.

.

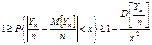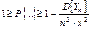В силу аддитивного свойства дисперсии, получаем

,

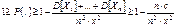
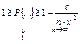
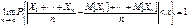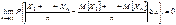g.

Следствие: Если 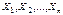– независимы и одинаково распределены, т.е. 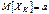, а 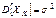, где k= 1, …, n, тогда

.

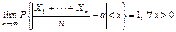Замечание. Предельные утверждения, сформулированные в теореме Чебышева и следствии к этой теореме носят название закона больших чисел (ЗБЧ). ЗБЧ утверждает, что с вероятностью приближающейся при n®¥ к 1, среднее арифметическое независимых слагаемых при определенных условиях становятся близким к константе.

Из утверждения последнего следствия получаем ЗБЧ в схеме Бернулли.

Теорема (Бернулли): Пусть 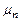– число успехов при n независимых испытаниях с вероятностью 0 < p < 1 в каждом испытании, тогда :

.

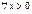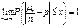Доказательство: Представим 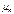в виде суммы независимых СВ 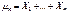, где 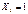, или при i-ом испытании произошел успех и 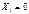, если при i-ом испытании произошел неуспех.

.

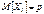Применяя следствие к теореме Чебышева, получаем утверждение к теореме Бернулли.

Понятие о теореме Ляпунова. Формулировка центральной предельной теоремы (ЦПТ).

Известно, что нормально распределенные СВ широко распространены на практике, объяснение дал Ляпунов (ЦПТ).

Если СВ Х представляет собой сумму очень большого числа взаимно независимых СВ влияние каждой из которых на всю сумму ничтожно мало, то СВ Х имеет распределение близкое к нормальному.

Приведем формулировку ЦПТ без доказательства.

Теорема(ЦПТ):Если СВ в последовательности 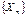, n = 1, 2, … независимы, одинаково распределены и имеют конечные 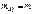, , 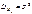то :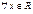

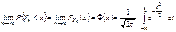
где 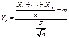– стандартизованное среднее арифметическое, n-независимых СВ в последовательности.

Замечание

Следствиями ЦПТ являются локальная и интегральная теоремы Муавра-Лапласса.

Общее: и для 50 и для 51:

Пусть неизвестная функция генеральной совокупности зависит от некоторого параметра 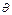. Нужно по наблюдениям оценить параметр. Для построения оценок используются статистики – функции от выборочных значений.

Примеры статистик. .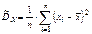

Эта оценка .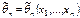

Будет рассматриваться, как приближенное значение параметра 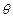.Замечание. Как правило, для оценки параметра 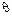можно использовать несколько статистик, получая при этом различные значения параметра 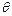. Как измерить «близость» оценки 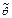к истинному значению 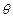? Как определить качество оценки? Комментарий: Качество оценки определяется не по одной конкретной выборке, а по всему мыслимому набору конкретных выборок, т.е. по случайному выборочному вектору 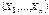, поэтому для установления качества полученных оценок моментов 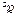, 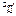следует во всех этих формулах заменить конкретные выборочные значения 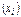на СВ X_i.

; ; .

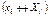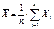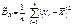Качество оценки устанавливают, проверяя, выполняются ли следующие три свойства (требования).Требования, предъявляемые к точечным оценкам:

1. Несмещенность, т.е. .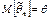

Это свойство желательно, но не обязательно. Часто полученная оценка бывает существенной, но ее можно поправить так, что она станет несмещенной.

Иногда оценка бывает смещенной, но асимптотически несмещенной, т.е. .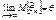

2. Состоятельность, т.е. .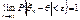

Это свойство является обязательным. Несостоятельные оценки не используются.

3. Эффективность.

а) Если оценк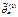и и 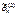– несмещенные, то 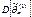и .

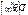Если 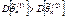, то оценка 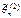более эффективна, чем .

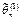б) Если оценк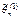и и 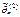– смещенные, тогда 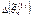и .

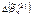Если 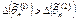, то оценка 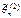более эффективная, чем .

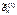Где 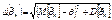– средний квадрат отклонения оценки.

Рассмотрим использование этих свойств на примерах выбора оценок МО и дисперсии:

50. Выборочное среднее: 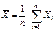является несмещенной и состоятельной оценкой МО генеральной совокупности (X₁ ,…, X_n ), причем каждое X_i совпадает с m и s².

а) Несмещенность. По определению выборочного вектора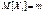

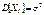, причем X_i – независимые в совокупности СВ, тогда вычислим

M[X^сред]=M[(1/n)åX_i]=(1/n)M[åX_i]=

(1/n)åM[X_i]=(1/n)nm 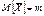g.

D[X^сред]=D[(1/n)åX_i]=(1/n²)D[åX_i]=

(1/n²)åD[X_i]=(1/n)ns²=s²/n

б) Состоятельность Воспользуемся неравенством Чебышева: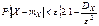

Применим это неравенство к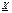

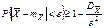
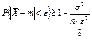
При n®¥ 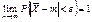,что и доказывает состоятельность .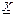