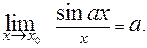Линейное векторное пространство. Базис и размерность линейного пространства
…Векторы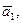 
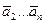называются линейно зависимыми, если существуют действительные числа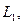 
…, 
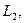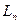(из которых по меньшей мере одно отлично от нуля), такие, что
(*)
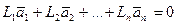в противном случае (т.е. когда таких чисел не существует) векторы называются линейно независимыми; другими словами, векторы линейно независимы, если равенство (*) выполняется лишь при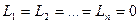 
Множество линейно независимых векторов называется базисом. Число векторов в базисе называется размерностью.
Пример 10.Показать, что векторы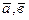 
и 
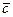образуют базис линейного векторного пространства и найти разложение вектора d в этом базисе:
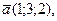
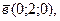
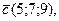
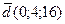
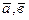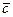Решение.Векторы и образуют базис тогда, когда выполнится условие
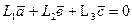при условии, что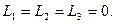 
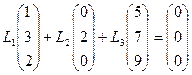
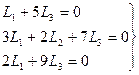
решая эту систему, получим, что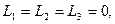 
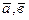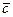значит и образуют базис. Найдем разложение вектора 
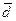базисе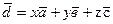 
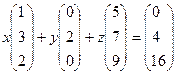
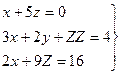
Решая эту систему, получаем: х = 80, у = -62, Z = - 16, а вместе с этим и разложение вектора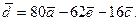 
Итак, координаты вектора 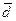в базисе 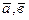и 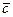равны 80, -62, -16.
Пример 11.По координатам точек найти: А(-5; 1; 6), В(1; 4; 3), С(6; 3; 9)
а) модель вектора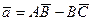 
= 
= 
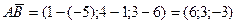
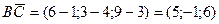
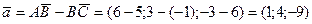
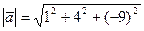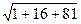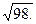
б) скалярное произведение векторов
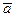и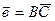 
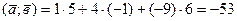
в) проекцию вектора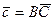 
на вектор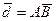 
пр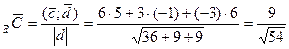 
г) координаты точки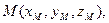 
делящей отрезок 
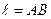в отношении 1 : 3;
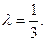Следовательно:
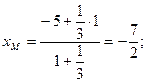
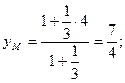
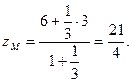(см. замечание)
Замечание! Деление отрезка в данном отношении. Даны две точки в пространстве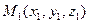 
и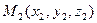 
. Найти координаты точки М, делящей отрезок 
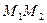в отношении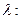 
По определению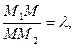 
где 
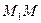и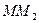 
величины направленных отрезков 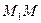и 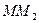оси, проходящей через точк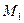и 
и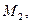 
поэтому = 
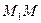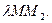
Координаты точки М находятся по формулам
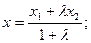
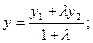
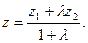
В частности, координаты середины отрезка определяются формулами
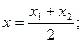
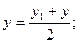
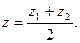
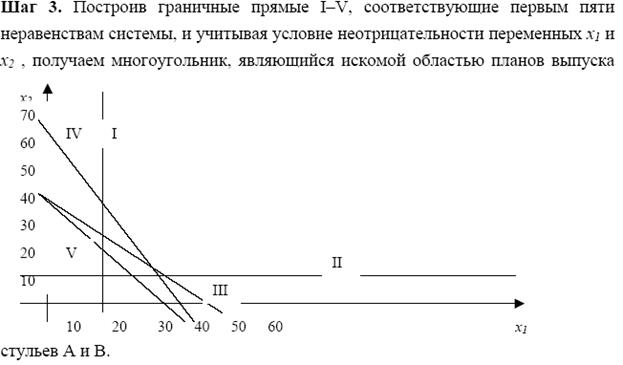
Задача.Предприятие производит изделия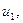 
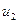и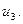 
За рассматриваемый промежуток времени плановый выпуск характеризуется вектором х = (10; 7; 4). Для изготовления изделий используется сырье 
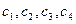и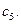 
В таблице приведены нормы расхода сырья на единицу каждого изделия. Вектор С = (7; 4; 5; 10; 2) задает стоимость единицы сырья каждого вида, а вектор Т = (3; 2; 3; 6; 3) – стоимость перевозки единицы сырья каждого вида.
| № п/п | Изделие | Расход сырья | ||||
 |  |  |  |  | ||
 | ||||||
| | ||||||
 |
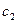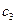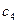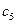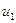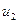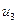1. Сколько единиц сырья каждого вида потребуется для выполнения плана?
2. Установить стоимость сырья, расходуемого на единицу изделия каждого вида.
3. Определить стоимость сырья, необходимого для выполнения плана.
4. Найти стоимость всего сырья с учетом его транспортировки.
Решение.Обозначим через А матрицу норм расхода сырья на единицу каждого изделия:
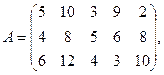
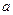через у – матрицу строку (вектор), характеризующую количество сырья каждого вида, требуемого для выполнения плана, тогда у =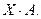 
Проведем вычисления:
.
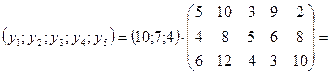
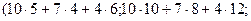
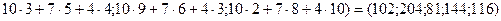Теперь можно вычислить стоимость сырья, расходуемого на единицу изделия i –го вида, обозначив ее матрицей-столбцом z =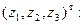 
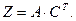
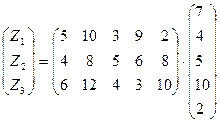Þ
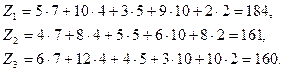
Таким образом, стоимость единицы изделия задается матрицей
Z = (184; 161; 160)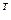 
Следовательно, стоимость всего сырья, необходимого для выполнения плана, можно вычислить по формуле
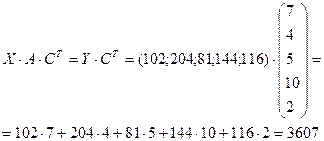
Для того, чтобы вычислить стоимость всего сырья с учетом его транспортировки, посчитаем сначала, во что обойдется его транспортировка, используя формулу
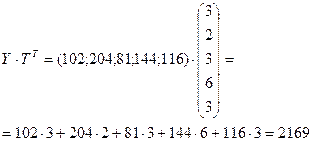
Следовательно, все расходы составят: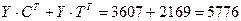 
Задача.
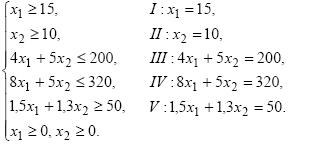
4.1. Пределы. Основные формулы
1. Свойства пределов
1) 
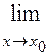(f(x) ± j(x))= 
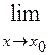f(x) ± 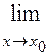j(x)
2) 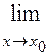(f(x) · j(x))=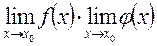 
3) 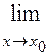c · f(x) = c · 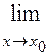f(x) где с = const
4) 
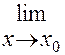(f (x))n = ( 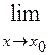f (x))n
5) 
= 
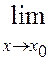
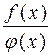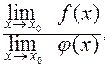
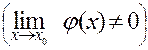
2. Первый замечательный предел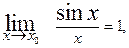 
в частности 